Predicting the Initial Conditions of the Universe using Deep Learning

Finding the initial conditions that led to the current state of the universe is challenging because it involves searching over a vast input space of initial conditions, along with modeling their evolution via tools such as N-body simulations which are computationally expensive. Deep learning has emerged as an alternate modeling tool that can learn the mapping between the linear input of an N-body simulation and the final nonlinear displacements at redshift zero, which can significantly accelerate the forward modeling. However, this does not help reduce the search space for initial conditions. In this paper, we demonstrate for the first time that a deep learning model can be trained for the reverse mapping. We train a V-Net based convolutional neural network, which outputs the linear displacement of an N-body system, given the current time nonlinear displacement and the cosmological parameters of the system. We demonstrate that this neural network accurately recovers the initial linear displacement field over a wide range of scales ($<1$-$2\%$ error up to nearly $k = 1\ \mathrm{Mpc}^{-1}\,h$), despite the ill-defined nature of the inverse problem at smaller scales. Specifically, smaller scales are dominated by nonlinear effects which makes the backward dynamics much more susceptible to numerical and computational errors leading to highly divergent backward trajectories and a one-to-many backward mapping. The results of our method motivate that neural network based models can act as good approximators of the initial linear states and their predictions can serve as good starting points for sampling-based methods to infer the initial states of the universe.

Simple lessons from complex learning: what a neural network model learns about cosmic structure formation

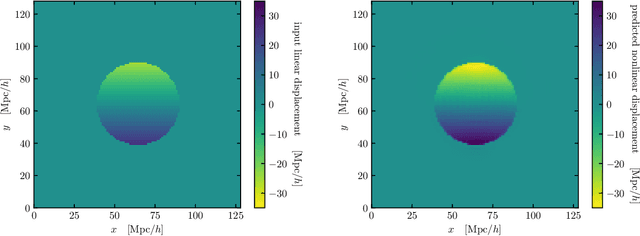
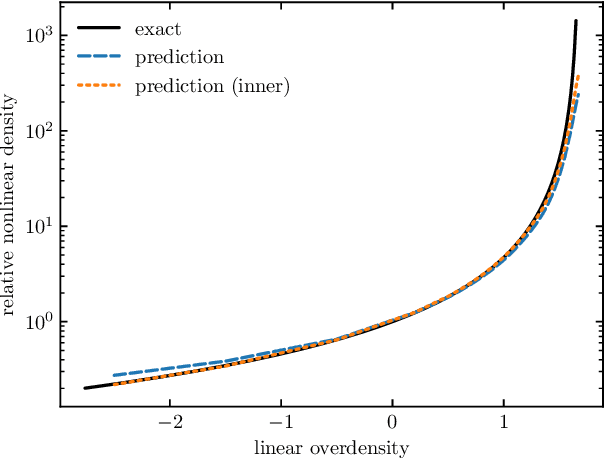
We train a neural network model to predict the full phase space evolution of cosmological N-body simulations. Its success implies that the neural network model is accurately approximating the Green's function expansion that relates the initial conditions of the simulations to its outcome at later times in the deeply nonlinear regime. We test the accuracy of this approximation by assessing its performance on well understood simple cases that have either known exact solutions or well understood expansions. These scenarios include spherical configurations, isolated plane waves, and two interacting plane waves: initial conditions that are very different from the Gaussian random fields used for training. We find our model generalizes well to these well understood scenarios, demonstrating that the networks have inferred general physical principles and learned the nonlinear mode couplings from the complex, random Gaussian training data. These tests also provide a useful diagnostic for finding the model's strengths and weaknesses, and identifying strategies for model improvement. We also test the model on initial conditions that contain only transverse modes, a family of modes that differ not only in their phases but also in their evolution from the longitudinal growing modes used in the training set. When the network encounters these initial conditions that are orthogonal to the training set, the model fails completely. In addition to these simple configurations, we evaluate the model's predictions for the density, displacement, and momentum power spectra with standard initial conditions for N-body simulations. We compare these summary statistics against N-body results and an approximate, fast simulation method called COLA. Our model achieves percent level accuracy at nonlinear scales of $k\sim 1\ \mathrm{Mpc}^{-1}\, h$, representing a significant improvement over COLA.

Field Level Neural Network Emulator for Cosmological N-body Simulations

We build a field level emulator for cosmic structure formation that is accurate in the nonlinear regime. Our emulator consists of two convolutional neural networks trained to output the nonlinear displacements and velocities of N-body simulation particles based on their linear inputs. Cosmology dependence is encoded in the form of style parameters at each layer of the neural network, enabling the emulator to effectively interpolate the outcomes of structure formation between different flat $\Lambda$CDM cosmologies over a wide range of background matter densities. The neural network architecture makes the model differentiable by construction, providing a powerful tool for fast field level inference. We test the accuracy of our method by considering several summary statistics, including the density power spectrum with and without redshift space distortions, the displacement power spectrum, the momentum power spectrum, the density bispectrum, halo abundances, and halo profiles with and without redshift space distortions. We compare these statistics from our emulator with the full N-body results, the COLA method, and a fiducial neural network with no cosmological dependence. We find our emulator gives accurate results down to scales of $k \sim 1\ \mathrm{Mpc}^{-1}\, h$, representing a considerable improvement over both COLA and the fiducial neural network. We also demonstrate that our emulator generalizes well to initial conditions containing primordial non-Gaussianity, without the need for any additional style parameters or retraining.