Field-level simulation-based inference with galaxy catalogs: the impact of systematic effects

It has been recently shown that a powerful way to constrain cosmological parameters from galaxy redshift surveys is to train graph neural networks to perform field-level likelihood-free inference without imposing cuts on scale. In particular, de Santi et al. (2023) developed models that could accurately infer the value of $\Omega_{\rm m}$ from catalogs that only contain the positions and radial velocities of galaxies that are robust to uncertainties in astrophysics and subgrid models. However, observations are affected by many effects, including 1) masking, 2) uncertainties in peculiar velocities and radial distances, and 3) different galaxy selections. Moreover, observations only allow us to measure redshift, intertwining galaxies' radial positions and velocities. In this paper we train and test our models on galaxy catalogs, created from thousands of state-of-the-art hydrodynamic simulations run with different codes from the CAMELS project, that incorporate these observational effects. We find that, although the presence of these effects degrades the precision and accuracy of the models, and increases the fraction of catalogs where the model breaks down, the fraction of galaxy catalogs where the model performs well is over 90 %, demonstrating the potential of these models to constrain cosmological parameters even when applied to real data.

Robust field-level likelihood-free inference with galaxies

We train graph neural networks to perform field-level likelihood-free inference using galaxy catalogs from state-of-the-art hydrodynamic simulations of the CAMELS project. Our models are rotationally, translationally, and permutation invariant and have no scale cutoff. By training on galaxy catalogs that only contain the 3D positions and radial velocities of approximately $1,000$ galaxies in tiny volumes of $(25~h^{-1}{\rm Mpc})^3$, our models achieve a precision of approximately $12$% when inferring the value of $\Omega_{\rm m}$. To test the robustness of our models, we evaluated their performance on galaxy catalogs from thousands of hydrodynamic simulations, each with different efficiencies of supernova and AGN feedback, run with five different codes and subgrid models, including IllustrisTNG, SIMBA, Astrid, Magneticum, and SWIFT-EAGLE. Our results demonstrate that our models are robust to astrophysics, subgrid physics, and subhalo/galaxy finder changes. Furthermore, we test our models on 1,024 simulations that cover a vast region in parameter space - variations in 5 cosmological and 23 astrophysical parameters - finding that the model extrapolates really well. Including both positions and velocities are key to building robust models, and our results indicate that our networks have likely learned an underlying physical relation that does not depend on galaxy formation and is valid on scales larger than, at least, $~\sim10~h^{-1}{\rm kpc}$.

The information of attribute uncertainties: what convolutional neural networks can learn about errors in input data

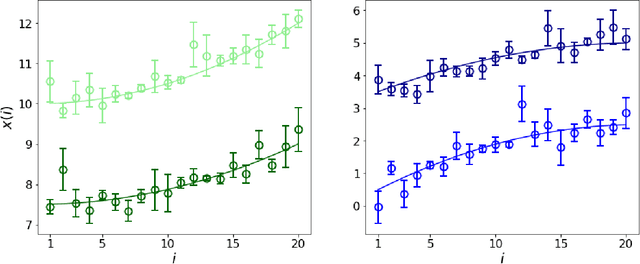
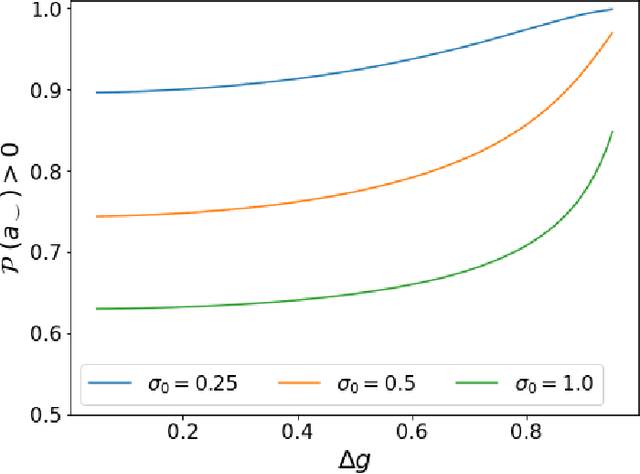
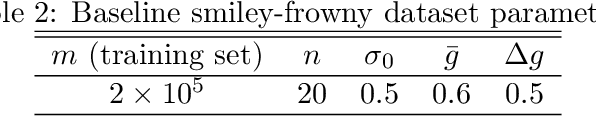
Errors in measurements are key to weighting the value of data, but are often neglected in Machine Learning (ML). We show how Convolutional Neural Networks (CNNs) are able to learn about the context and patterns of signal and noise, leading to improvements in the performance of classification methods. We construct a model whereby two classes of objects follow an underlying Gaussian distribution, and where the features (the input data) have varying, but known, levels of noise. This model mimics the nature of scientific data sets, where the noises arise as realizations of some random processes whose underlying distributions are known. The classification of these objects can then be performed using standard statistical techniques (e.g., least-squares minimization or Markov-Chain Monte Carlo), as well as ML techniques. This allows us to take advantage of a maximum likelihood approach to object classification, and to measure the amount by which the ML methods are incorporating the information in the input data uncertainties. We show that, when each data point is subject to different levels of noise (i.e., noises with different distribution functions), that information can be learned by the CNNs, raising the ML performance to at least the same level of the least-squares method -- and sometimes even surpassing it. Furthermore, we show that, with varying noise levels, the confidence of the ML classifiers serves as a proxy for the underlying cumulative distribution function, but only if the information about specific input data uncertainties is provided to the CNNs.