Opportunities in AI/ML for the Rubin LSST Dark Energy Science Collaboration

The Vera C. Rubin Observatory's Legacy Survey of Space and Time (LSST) will produce unprecedented volumes of heterogeneous astronomical data (images, catalogs, and alerts) that challenge traditional analysis pipelines. The LSST Dark Energy Science Collaboration (DESC) aims to derive robust constraints on dark energy and dark matter from these data, requiring methods that are statistically powerful, scalable, and operationally reliable. Artificial intelligence and machine learning (AI/ML) are already embedded across DESC science workflows, from photometric redshifts and transient classification to weak lensing inference and cosmological simulations. Yet their utility for precision cosmology hinges on trustworthy uncertainty quantification, robustness to covariate shift and model misspecification, and reproducible integration within scientific pipelines. This white paper surveys the current landscape of AI/ML across DESC's primary cosmological probes and cross-cutting analyses, revealing that the same core methodologies and fundamental challenges recur across disparate science cases. Since progress on these cross-cutting challenges would benefit multiple probes simultaneously, we identify key methodological research priorities, including Bayesian inference at scale, physics-informed methods, validation frameworks, and active learning for discovery. With an eye on emerging techniques, we also explore the potential of the latest foundation model methodologies and LLM-driven agentic AI systems to reshape DESC workflows, provided their deployment is coupled with rigorous evaluation and governance. Finally, we discuss critical software, computing, data infrastructure, and human capital requirements for the successful deployment of these new methodologies, and consider associated risks and opportunities for broader coordination with external actors.

Transfer Learning Beyond the Standard Model

Machine learning enables powerful cosmological inference but typically requires many high-fidelity simulations covering many cosmological models. Transfer learning offers a way to reduce the simulation cost by reusing knowledge across models. We show that pre-training on the standard model of cosmology, $\Lambda$CDM, and fine-tuning on various beyond-$\Lambda$CDM scenarios -- including massive neutrinos, modified gravity, and primordial non-Gaussianities -- can enable inference with significantly fewer beyond-$\Lambda$CDM simulations. However, we also show that negative transfer can occur when strong physical degeneracies exist between $\Lambda$CDM and beyond-$\Lambda$CDM parameters. We consider various transfer architectures, finding that including bottleneck structures provides the best performance. Our findings illustrate the opportunities and pitfalls of foundation-model approaches in physics: pre-training can accelerate inference, but may also hinder learning new physics.

The optical and infrared are connected

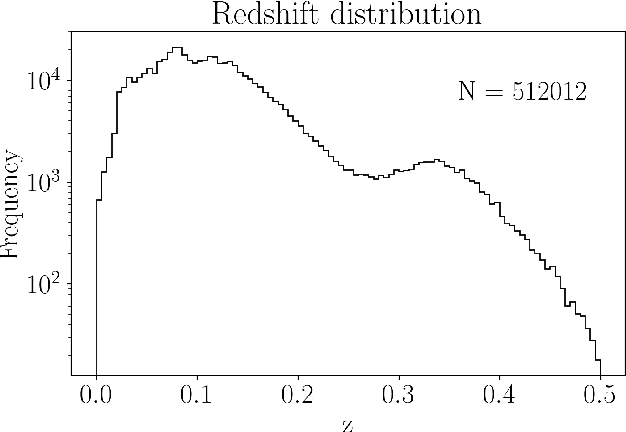
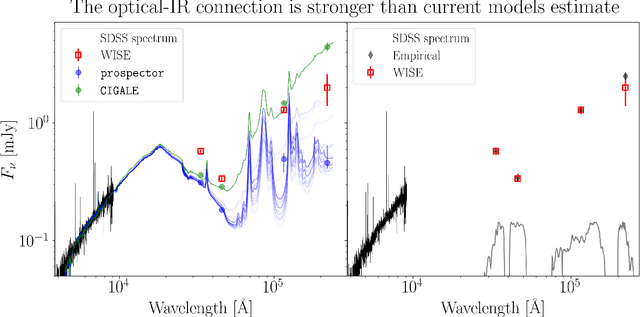
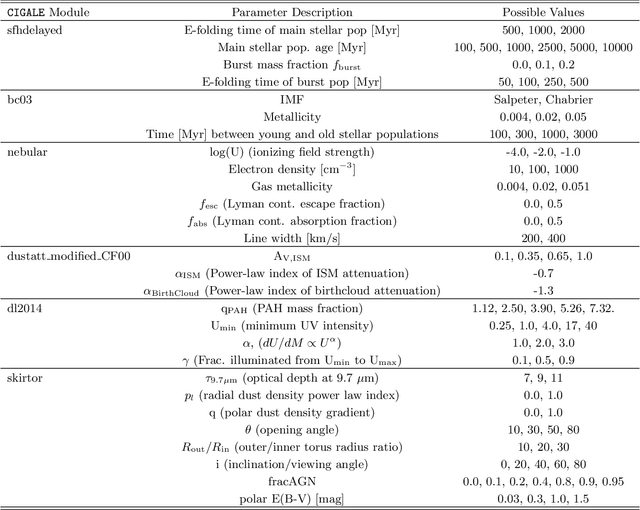
Galaxies are often modelled as composites of separable components with distinct spectral signatures, implying that different wavelength ranges are only weakly correlated. They are not. We present a data-driven model which exploits subtle correlations between physical processes to accurately predict infrared (IR) WISE photometry from a neural summary of optical SDSS spectra. The model achieves accuracies of $\chi^2_N \approx 1$ for all photometric bands in WISE, as well as good colors. We are also able to tightly constrain typically IR-derived properties, e.g. the bolometric luminosities of AGN and dust parameters such as $\mathrm{q_{PAH}}$. We find that current SED-fitting methods are incapable of making comparable predictions, and that model misspecification often leads to correlated biases in star-formation rates and AGN luminosities. To help improve SED models, we determine what features of the optical spectrum are responsible for our improved predictions, and identify several lines (CaII, SrII, FeI, [OII] and H$\alpha$), which point to the complex chronology of star formation and chemical enrichment being incorrectly modelled.

Path-minimizing Latent ODEs for improved extrapolation and inference

Latent ODE models provide flexible descriptions of dynamic systems, but they can struggle with extrapolation and predicting complicated non-linear dynamics. The latent ODE approach implicitly relies on encoders to identify unknown system parameters and initial conditions, whereas the evaluation times are known and directly provided to the ODE solver. This dichotomy can be exploited by encouraging time-independent latent representations. By replacing the common variational penalty in latent space with an $\ell_2$ penalty on the path length of each system, the models learn data representations that can easily be distinguished from those of systems with different configurations. This results in faster training, smaller models, more accurate interpolation and long-time extrapolation compared to the baseline ODE models with GRU, RNN, and LSTM encoder/decoders on tests with damped harmonic oscillator, self-gravitating fluid, and predator-prey systems. We also demonstrate superior results for simulation-based inference of the Lotka-Volterra parameters and initial conditions by using the latents as data summaries for a conditional normalizing flow. Our change to the training loss is agnostic to the specific recognition network used by the decoder and can therefore easily be adopted by other latent ODE models.

Multiscale Feature Attribution for Outliers

Machine learning techniques can automatically identify outliers in massive datasets, much faster and more reproducible than human inspection ever could. But finding such outliers immediately leads to the question: which features render this input anomalous? We propose a new feature attribution method, Inverse Multiscale Occlusion, that is specifically designed for outliers, for which we have little knowledge of the type of features we want to identify and expect that the model performance is questionable because anomalous test data likely exceed the limits of the training data. We demonstrate our method on outliers detected in galaxy spectra from the Dark Energy Survey Instrument and find its results to be much more interpretable than alternative attribution approaches.

$\texttt{Mangrove}$: Learning Galaxy Properties from Merger Trees

Efficiently mapping baryonic properties onto dark matter is a major challenge in astrophysics. Although semi-analytic models (SAMs) and hydrodynamical simulations have made impressive advances in reproducing galaxy observables across cosmologically significant volumes, these methods still require significant computation times, representing a barrier to many applications. Graph Neural Networks (GNNs) have recently proven to be the natural choice for learning physical relations. Among the most inherently graph-like structures found in astrophysics are the dark matter merger trees that encode the evolution of dark matter halos. In this paper we introduce a new, graph-based emulator framework, $\texttt{Mangrove}$, and show that it emulates the galactic stellar mass, cold gas mass and metallicity, instantaneous and time-averaged star formation rate, and black hole mass -- as predicted by a SAM -- with root mean squared error up to two times lower than other methods across a $(75 Mpc/h)^3$ simulation box in 40 seconds, 4 orders of magnitude faster than the SAM. We show that $\texttt{Mangrove}$ allows for quantification of the dependence of galaxy properties on merger history. We compare our results to the current state of the art in the field and show significant improvements for all target properties. $\texttt{Mangrove}$ is publicly available.

Accelerated Bayesian SED Modeling using Amortized Neural Posterior Estimation

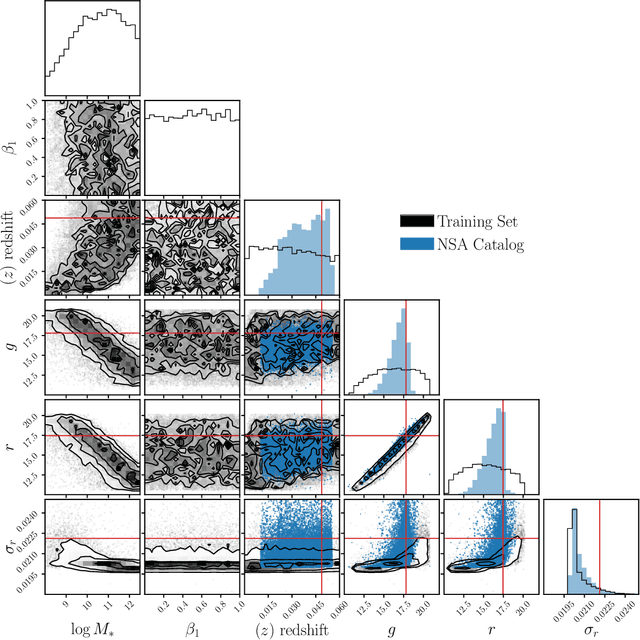
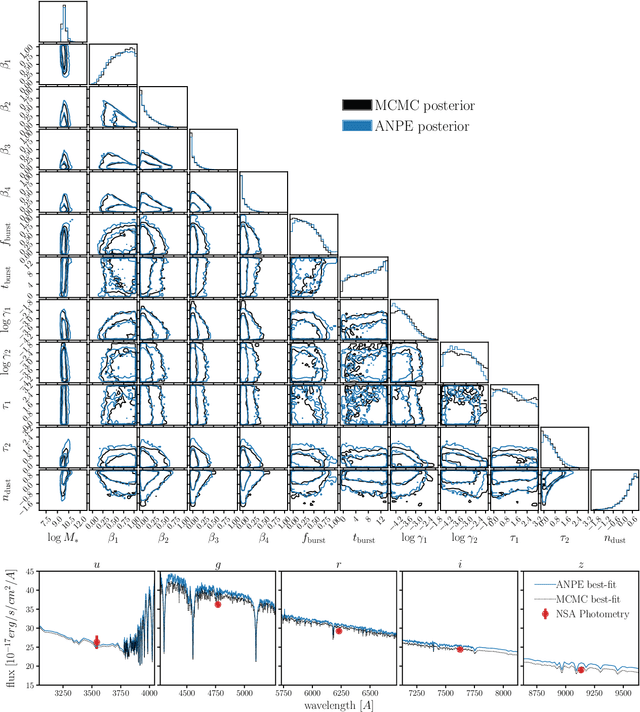
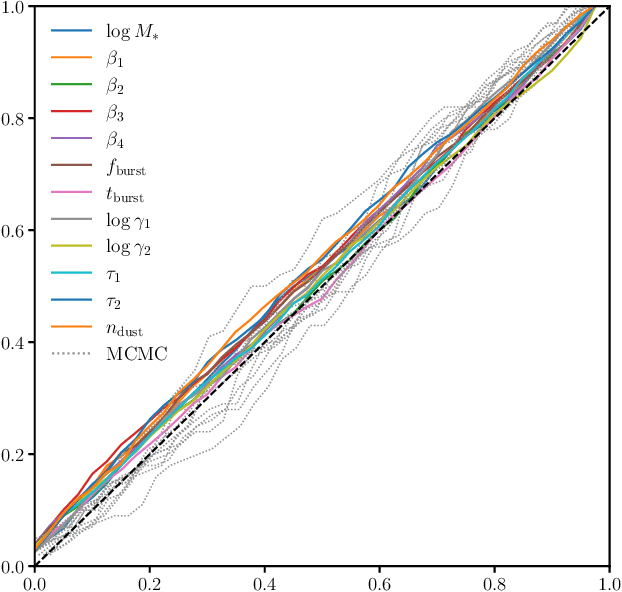
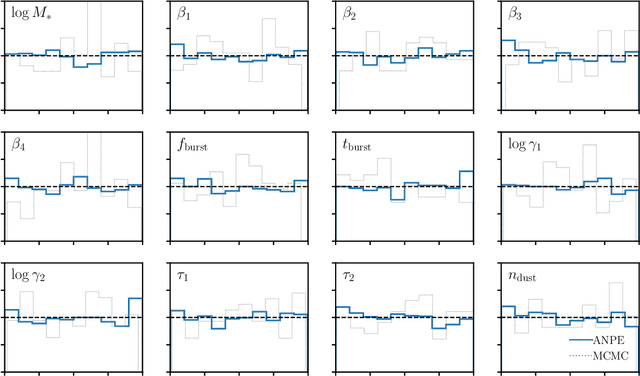
State-of-the-art spectral energy distribution (SED) analyses use a Bayesian framework to infer the physical properties of galaxies from observed photometry or spectra. They require sampling from a high-dimensional space of SED model parameters and take $>10-100$ CPU hours per galaxy, which renders them practically infeasible for analyzing the $billions$ of galaxies that will be observed by upcoming galaxy surveys ($e.g.$ DESI, PFS, Rubin, Webb, and Roman). In this work, we present an alternative scalable approach to rigorous Bayesian inference using Amortized Neural Posterior Estimation (ANPE). ANPE is a simulation-based inference method that employs neural networks to estimate the posterior probability distribution over the full range of observations. Once trained, it requires no additional model evaluations to estimate the posterior. We present, and publicly release, ${\rm SED}{flow}$, an ANPE method to produce posteriors of the recent Hahn et al. (2022) SED model from optical photometry. ${\rm SED}{flow}$ takes ${\sim}1$ $second~per~galaxy$ to obtain the posterior distributions of 12 model parameters, all of which are in excellent agreement with traditional Markov Chain Monte Carlo sampling results. We also apply ${\rm SED}{flow}$ to 33,884 galaxies in the NASA-Sloan Atlas and publicly release their posteriors: see https://changhoonhahn.github.io/SEDflow.

Graph Neural Network-based Resource Allocation Strategies for Multi-Object Spectroscopy

Resource allocation problems are often approached with linear programming techniques. But many concrete allocation problems in the experimental and observational sciences cannot or should not be expressed in the form of linear objective functions. Even if the objective is linear, its parameters may not be known beforehand because they depend on the results of the experiment for which the allocation is to be determined. To address these challenges, we present a bipartite Graph Neural Network architecture for trainable resource allocation strategies. Items of value and constraints form the two sets of graph nodes, which are connected by edges corresponding to possible allocations. The GNN is trained on simulations or past problem occurrences to maximize any user-supplied, scientifically motivated objective function, augmented by an infeasibility penalty. The amount of feasibility violation can be tuned in relation to any available slack in the system. We apply this method to optimize the astronomical target selection strategy for the highly multiplexed Subaru Prime Focus Spectrograph instrument, where it shows superior results to direct gradient descent optimization and extends the capabilities of the currently employed solver which uses linear objective functions. The development of this method enables fast adjustment and deployment of allocation strategies, statistical analyses of allocation patterns, and fully differentiable, science-driven solutions for resource allocation problems.

Unsupervised Resource Allocation with Graph Neural Networks

We present an approach for maximizing a global utility function by learning how to allocate resources in an unsupervised way. We expect interactions between allocation targets to be important and therefore propose to learn the reward structure for near-optimal allocation policies with a GNN. By relaxing the resource constraint, we can employ gradient-based optimization in contrast to more standard evolutionary algorithms. Our algorithm is motivated by a problem in modern astronomy, where one needs to select-based on limited initial information-among $10^9$ galaxies those whose detailed measurement will lead to optimal inference of the composition of the universe. Our technique presents a way of flexibly learning an allocation strategy by only requiring forward simulators for the physics of interest and the measurement process. We anticipate that our technique will also find applications in a range of resource allocation problems.

$\texttt{deep21}$: a Deep Learning Method for 21cm Foreground Removal

We seek to remove foreground contaminants from 21cm intensity mapping observations. We demonstrate that a deep convolutional neural network (CNN) with a UNet architecture and three-dimensional convolutions, trained on simulated observations, can effectively separate frequency and spatial patterns of the cosmic neutral hydrogen (HI) signal from foregrounds in the presence of noise. Cleaned maps recover cosmological clustering statistics within 10% at all relevant angular scales and frequencies. This amounts to a reduction in prediction variance of over an order of magnitude on small angular scales ($\ell > 300$), and improved accuracy for small radial scales ($k_{\parallel} > 0.17\ \rm h\ Mpc^{-1})$ compared to standard Principal Component Analysis (PCA) methods. We estimate posterior confidence intervals for the network's prediction by training an ensemble of UNets. Our approach demonstrates the feasibility of analyzing 21cm intensity maps, as opposed to derived summary statistics, for upcoming radio experiments, as long as the simulated foreground model is sufficiently realistic. We provide the code used for this analysis on $\href{https://github.com/tlmakinen/deep21}{\rm GitHub}$, as well as a browser-based tutorial for the experiment and UNet model via the accompanying $\href{http://bit.ly/deep21-colab}{\rm Colab\ notebook}$.