Kernel-, mean- and noise-marginalised Gaussian processes for exoplanet transits and $H_0$ inference

Using a fully Bayesian approach, Gaussian Process regression is extended to include marginalisation over the kernel choice and kernel hyperparameters. In addition, Bayesian model comparison via the evidence enables direct kernel comparison. The calculation of the joint posterior was implemented with a transdimensional sampler which simultaneously samples over the discrete kernel choice and their hyperparameters by embedding these in a higher-dimensional space, from which samples are taken using nested sampling. This method was explored on synthetic data from exoplanet transit light curve simulations. The true kernel was recovered in the low noise region while no kernel was preferred for larger noise. Furthermore, inference of the physical exoplanet hyperparameters was conducted. In the high noise region, either the bias in the posteriors was removed, the posteriors were broadened or the accuracy of the inference was increased. In addition, the uncertainty in mean function predictive distribution increased due to the uncertainty in the kernel choice. Subsequently, the method was extended to marginalisation over mean functions and noise models and applied to the inference of the present-day Hubble parameter, $H_0$, from real measurements of the Hubble parameter as a function of redshift, derived from the cosmologically model-independent cosmic chronometer and {\Lambda}CDM-dependent baryon acoustic oscillation observations. The inferred $H_0$ values from the cosmic chronometers, baryon acoustic oscillations and combined datasets are $H_0$ = 66$\pm$6 km/s/Mpc, $H_0$ = 67$\pm$10 km/s/Mpc and $H_0$ = 69$\pm$6 km/s/Mpc, respectively. The kernel posterior of the cosmic chronometers dataset prefers a non-stationary linear kernel. Finally, the datasets are shown to be not in tension with ln(R)=12.17$\pm$0.02.

Robust Simulation-Based Inference in Cosmology with Bayesian Neural Networks

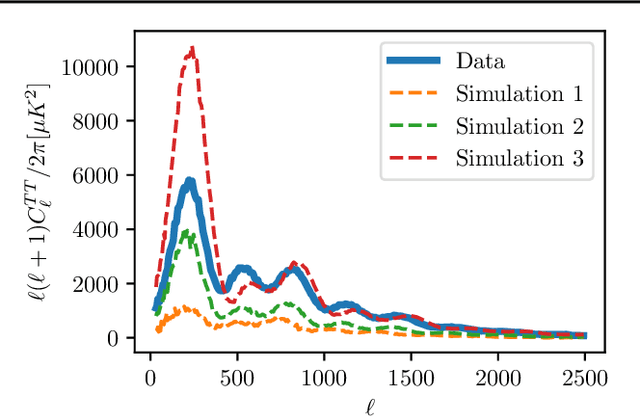
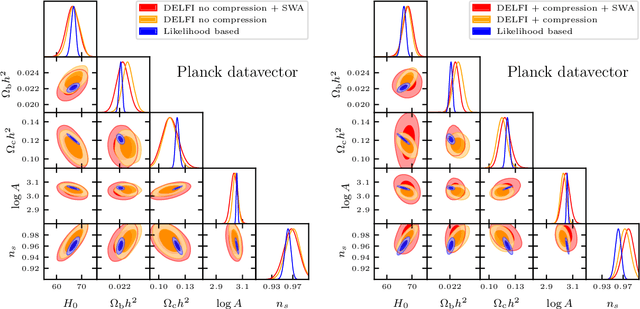
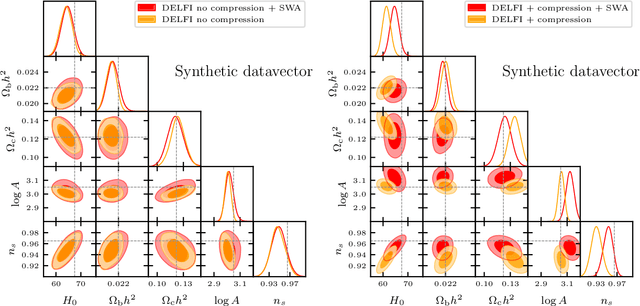
Simulation-based inference (SBI) is rapidly establishing itself as a standard machine learning technique for analyzing data in cosmological surveys. Despite continual improvements to the quality of density estimation by learned models, applications of such techniques to real data are entirely reliant on the generalization power of neural networks far outside the training distribution, which is mostly unconstrained. Due to the imperfections in scientist-created simulations, and the large computational expense of generating all possible parameter combinations, SBI methods in cosmology are vulnerable to such generalization issues. Here, we discuss the effects of both issues, and show how using a Bayesian neural network framework for training SBI can mitigate biases, and result in more reliable inference outside the training set. We introduce cosmoSWAG, the first application of Stochastic Weight Averaging to cosmology, and apply it to SBI trained for inference on the cosmic microwave background.

Split personalities in Bayesian Neural Networks: the case for full marginalisation

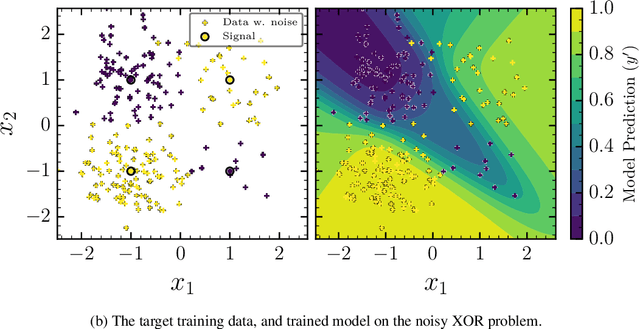
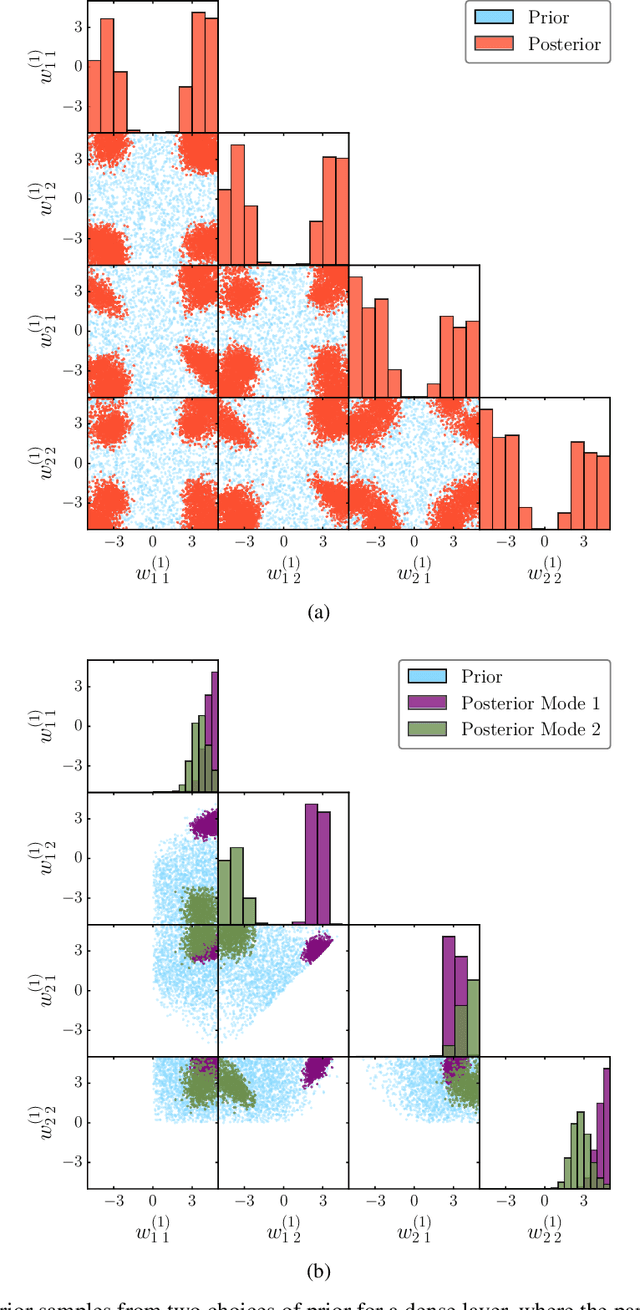
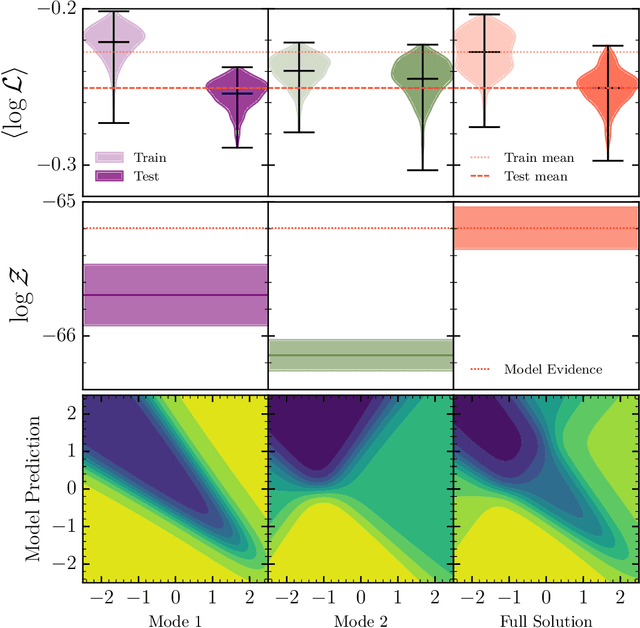
The true posterior distribution of a Bayesian neural network is massively multimodal. Whilst most of these modes are functionally equivalent, we demonstrate that there remains a level of real multimodality that manifests in even the simplest neural network setups. It is only by fully marginalising over all posterior modes, using appropriate Bayesian sampling tools, that we can capture the split personalities of the network. The ability of a network trained in this manner to reason between multiple candidate solutions dramatically improves the generalisability of the model, a feature we contend is not consistently captured by alternative approaches to the training of Bayesian neural networks. We provide a concise minimal example of this, which can provide lessons and a future path forward for correctly utilising the explainability and interpretability of Bayesian neural networks.