Split personalities in Bayesian Neural Networks: the case for full marginalisation

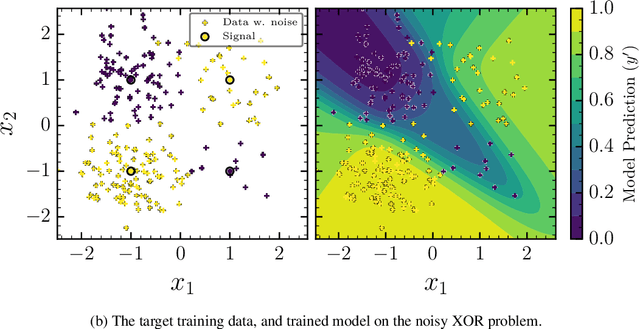
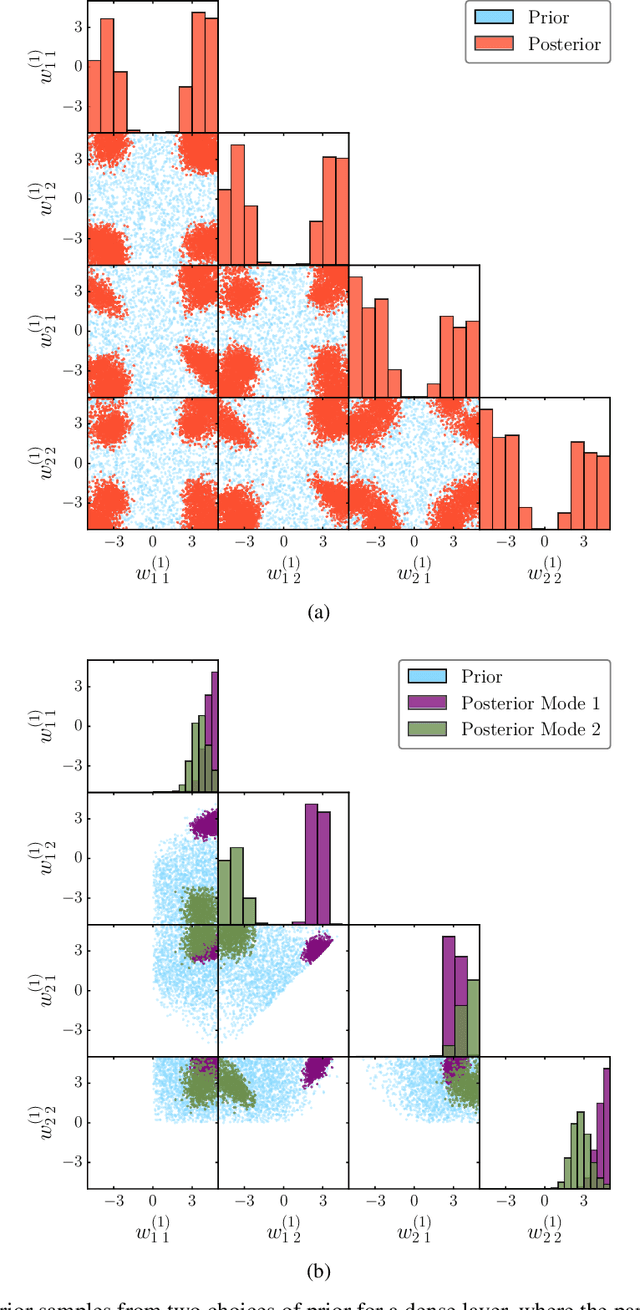
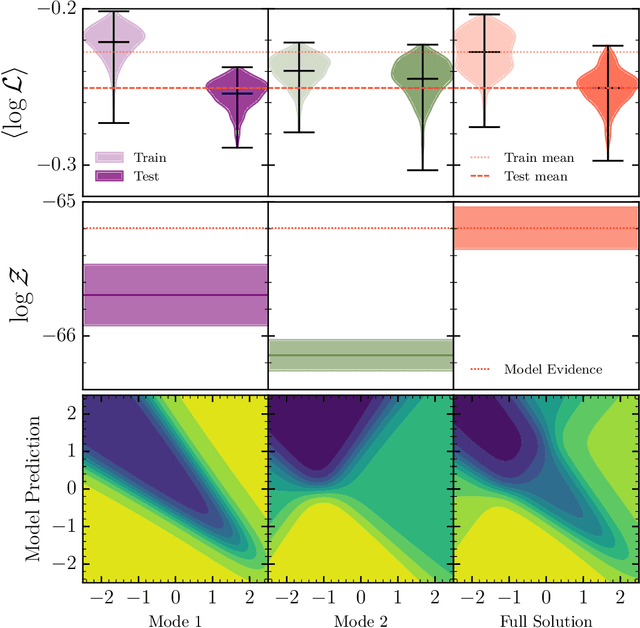
The true posterior distribution of a Bayesian neural network is massively multimodal. Whilst most of these modes are functionally equivalent, we demonstrate that there remains a level of real multimodality that manifests in even the simplest neural network setups. It is only by fully marginalising over all posterior modes, using appropriate Bayesian sampling tools, that we can capture the split personalities of the network. The ability of a network trained in this manner to reason between multiple candidate solutions dramatically improves the generalisability of the model, a feature we contend is not consistently captured by alternative approaches to the training of Bayesian neural networks. We provide a concise minimal example of this, which can provide lessons and a future path forward for correctly utilising the explainability and interpretability of Bayesian neural networks.

Compromise-free Bayesian neural networks

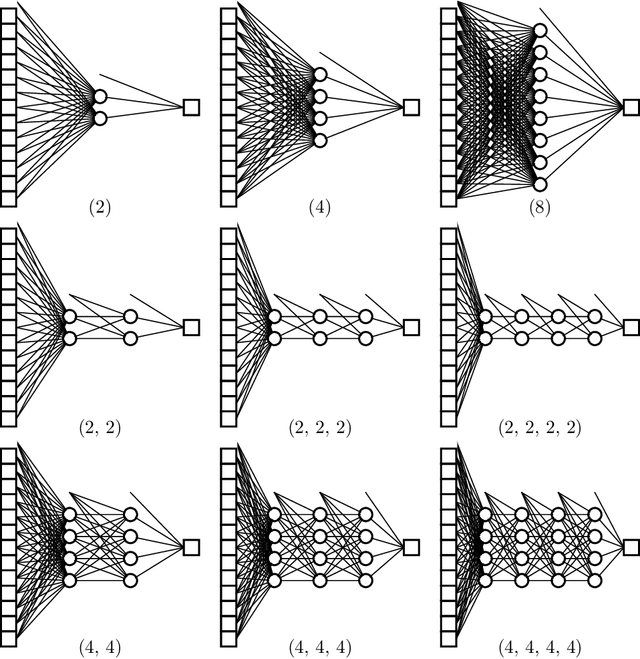
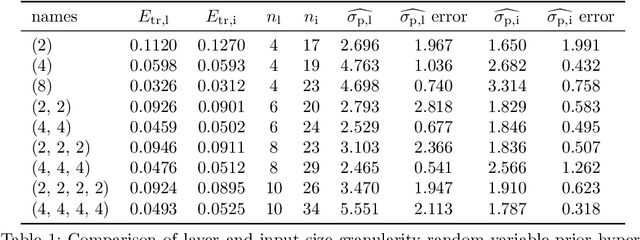
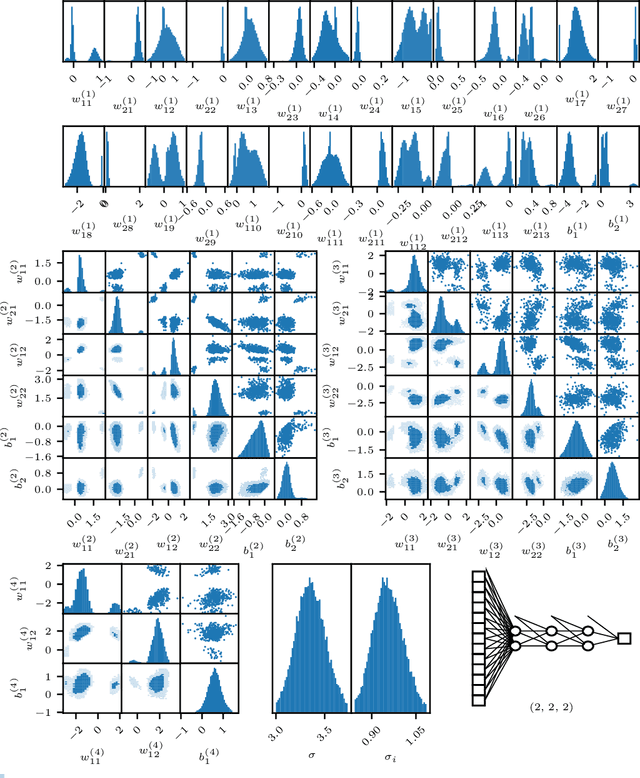
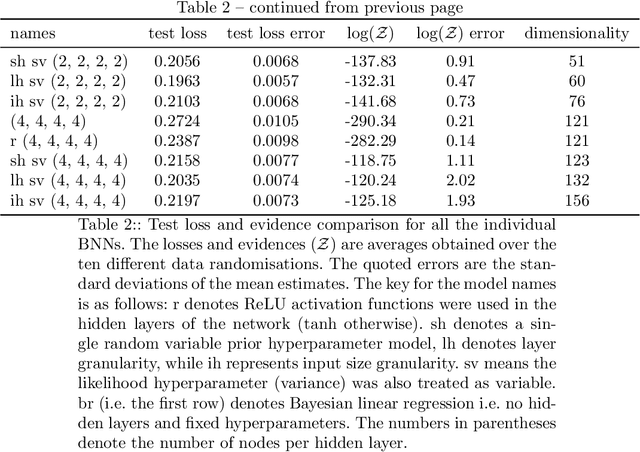
We conduct a thorough analysis of the relationship between the out-of-sample performance and the Bayesian evidence of Bayesian neural networks (BNNs) using the Boston housing dataset, as well as looking at the performance of ensembles of BNNs. We numerically sample without compromise the full network posterior and obtain estimates of the Bayesian evidence using the publicly available version of the nested sampling algorithm PolyChord$^1$ (Handley et al., 2015a,b), considering network models with up to 156 trainable parameters$^2$ (Javid and Handley, 2020). The networks have between zero and four hidden layers, either $\tanh$ or ReLU activation functions, and with and without hierarchical priors (MacKay, 1992c; Neal, 2012). The ensembles of BNNs are obtained by determining the posterior distribution over networks, from the posterior samples of individual BNNs re-weighted by the associated Bayesian evidence values. From the out-of-sample performance of the BNNs with ReLU activations, it is clear that they outperform BNNs of the same architecture with tanh activations, and evidence values corresponding to the former reflect this in their relatively high values. Looking at the models with hierarchical priors, there is a good correlation between out-of-sample performance and evidence, as was found in MacKay (1992c), as well as a remarkable symmetry between the evidence versus model size and out-of-sample performance versus model size planes. The BNNs predictively outperform the equivalent neural networks trained with a traditional backpropagation approach, and Bayesian marginalising/ensembling over architectures acts to further improve performance. 1: https://github.com/PolyChord/PolyChordLite 2: https://github.com/SuperKam91/bnn

Bayesian sparse reconstruction: a brute-force approach to astronomical imaging and machine learning

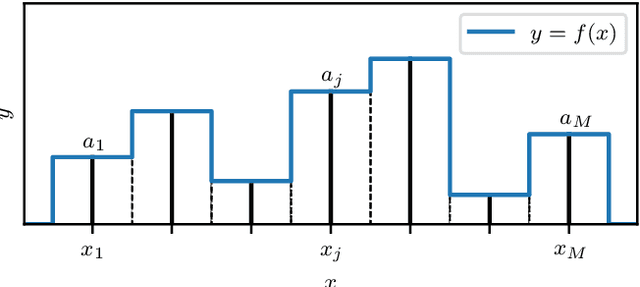
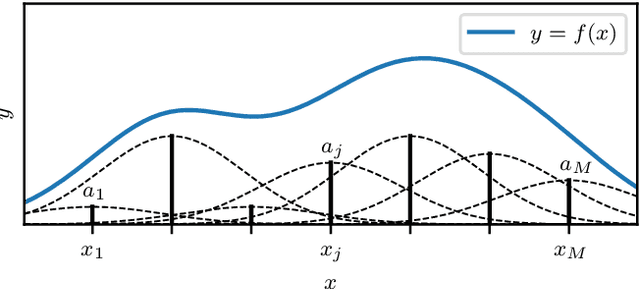
We present a principled Bayesian framework for signal reconstruction, in which the signal is modelled by basis functions whose number (and form, if required) is determined by the data themselves. This approach is based on a Bayesian interpretation of conventional sparse reconstruction and regularisation techniques, in which sparsity is imposed through priors via Bayesian model selection. We demonstrate our method for noisy 1- and 2-dimensional signals, including astronomical images. Furthermore, by using a product-space approach, the number and type of basis functions can be treated as integer parameters and their posterior distributions sampled directly. We show that order-of-magnitude increases in computational efficiency are possible from this technique compared to calculating the Bayesian evidences separately, and that further computational gains are possible using it in combination with dynamic nested sampling. Our approach can be readily applied to neural networks, where it allows the network architecture to be determined by the data in a principled Bayesian manner by treating the number of nodes and hidden layers as parameters.

BAMBI: blind accelerated multimodal Bayesian inference

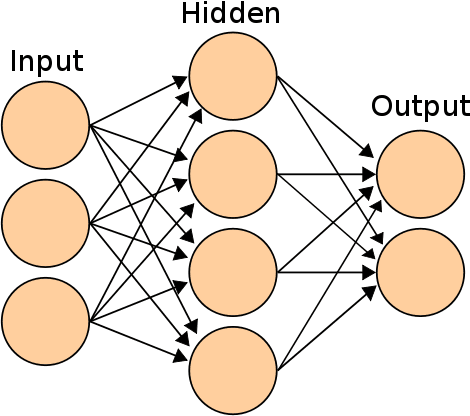
In this paper we present an algorithm for rapid Bayesian analysis that combines the benefits of nested sampling and artificial neural networks. The blind accelerated multimodal Bayesian inference (BAMBI) algorithm implements the MultiNest package for nested sampling as well as the training of an artificial neural network (NN) to learn the likelihood function. In the case of computationally expensive likelihoods, this allows the substitution of a much more rapid approximation in order to increase significantly the speed of the analysis. We begin by demonstrating, with a few toy examples, the ability of a NN to learn complicated likelihood surfaces. BAMBI's ability to decrease running time for Bayesian inference is then demonstrated in the context of estimating cosmological parameters from Wilkinson Microwave Anisotropy Probe and other observations. We show that valuable speed increases are achieved in addition to obtaining NNs trained on the likelihood functions for the different model and data combinations. These NNs can then be used for an even faster follow-up analysis using the same likelihood and different priors. This is a fully general algorithm that can be applied, without any pre-processing, to other problems with computationally expensive likelihood functions.