Split personalities in Bayesian Neural Networks: the case for full marginalisation

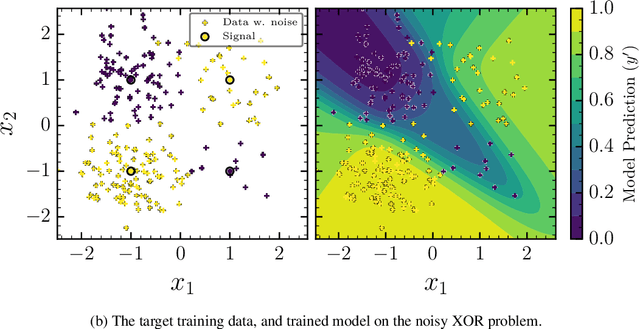
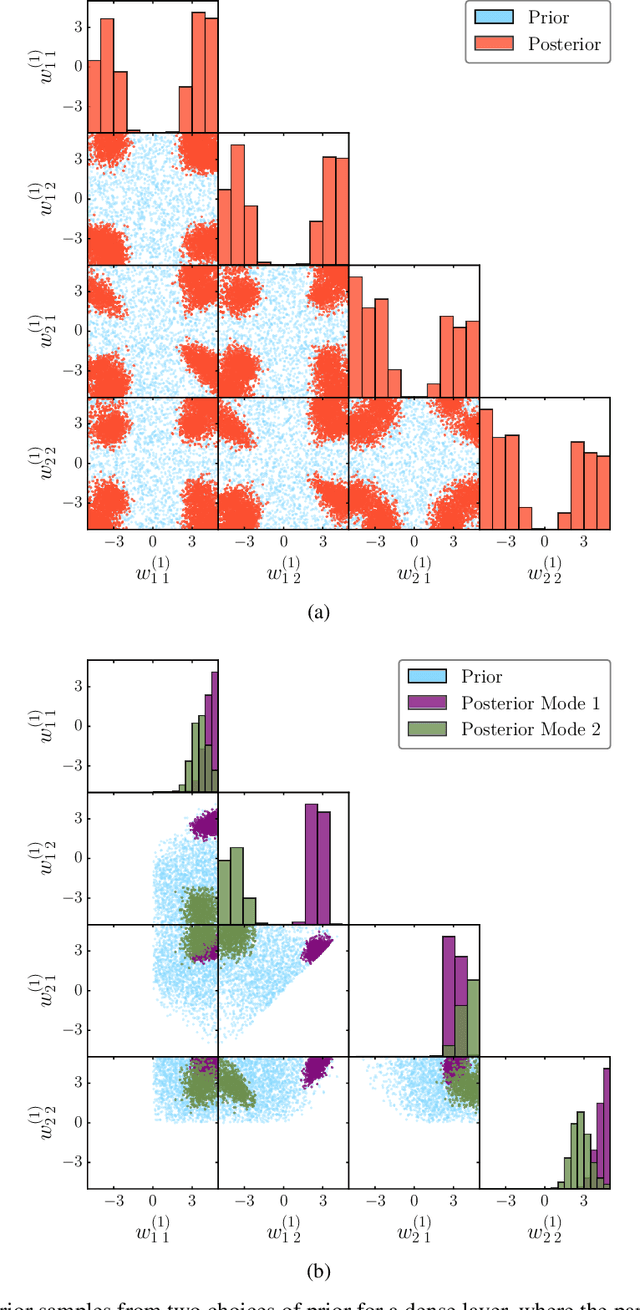
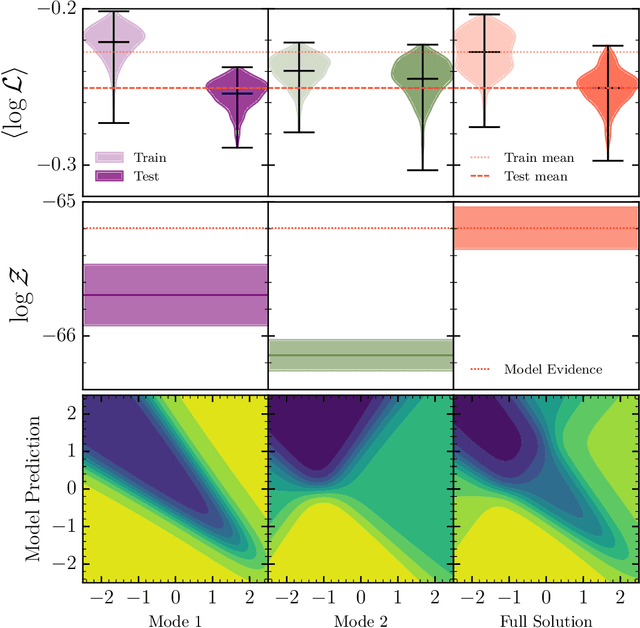
The true posterior distribution of a Bayesian neural network is massively multimodal. Whilst most of these modes are functionally equivalent, we demonstrate that there remains a level of real multimodality that manifests in even the simplest neural network setups. It is only by fully marginalising over all posterior modes, using appropriate Bayesian sampling tools, that we can capture the split personalities of the network. The ability of a network trained in this manner to reason between multiple candidate solutions dramatically improves the generalisability of the model, a feature we contend is not consistently captured by alternative approaches to the training of Bayesian neural networks. We provide a concise minimal example of this, which can provide lessons and a future path forward for correctly utilising the explainability and interpretability of Bayesian neural networks.

Compromise-free Bayesian neural networks

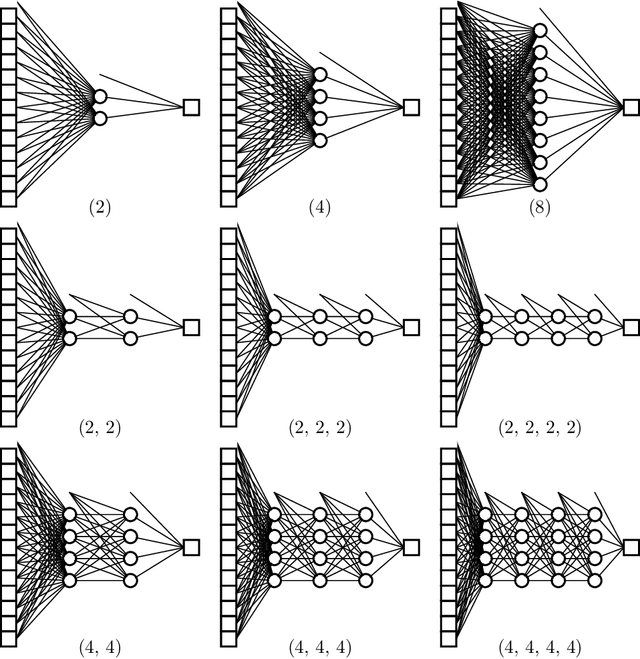
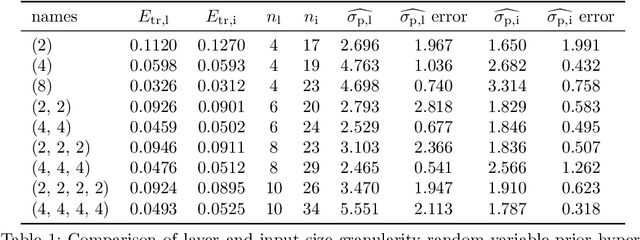
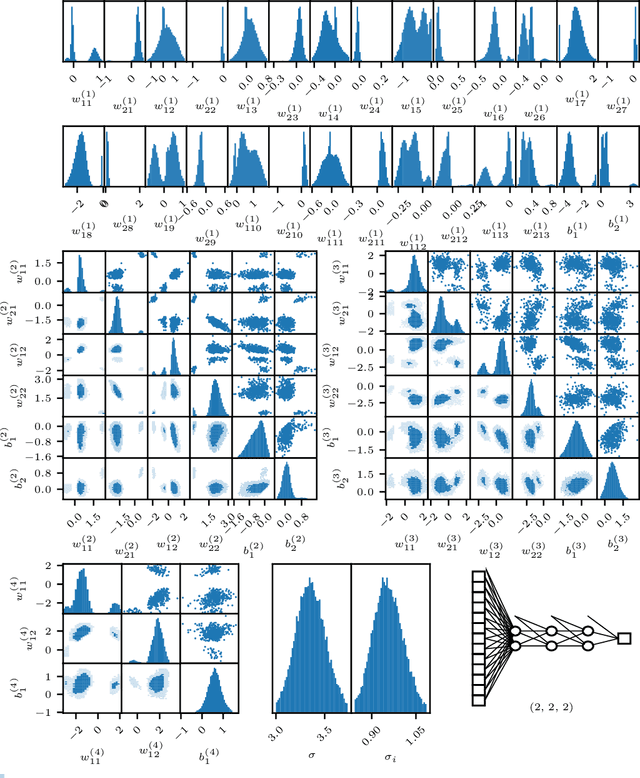
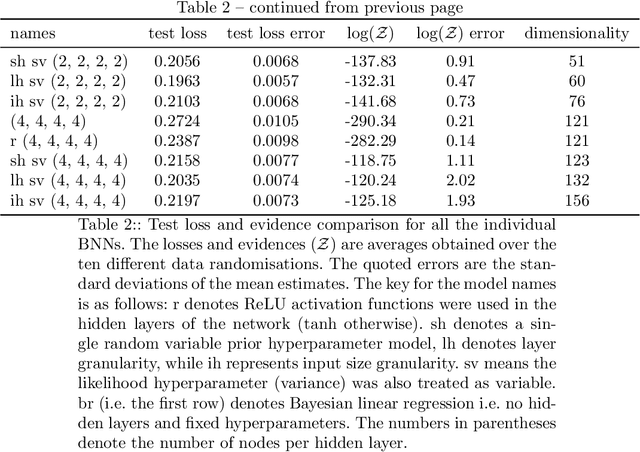
We conduct a thorough analysis of the relationship between the out-of-sample performance and the Bayesian evidence of Bayesian neural networks (BNNs) using the Boston housing dataset, as well as looking at the performance of ensembles of BNNs. We numerically sample without compromise the full network posterior and obtain estimates of the Bayesian evidence using the publicly available version of the nested sampling algorithm PolyChord$^1$ (Handley et al., 2015a,b), considering network models with up to 156 trainable parameters$^2$ (Javid and Handley, 2020). The networks have between zero and four hidden layers, either $\tanh$ or ReLU activation functions, and with and without hierarchical priors (MacKay, 1992c; Neal, 2012). The ensembles of BNNs are obtained by determining the posterior distribution over networks, from the posterior samples of individual BNNs re-weighted by the associated Bayesian evidence values. From the out-of-sample performance of the BNNs with ReLU activations, it is clear that they outperform BNNs of the same architecture with tanh activations, and evidence values corresponding to the former reflect this in their relatively high values. Looking at the models with hierarchical priors, there is a good correlation between out-of-sample performance and evidence, as was found in MacKay (1992c), as well as a remarkable symmetry between the evidence versus model size and out-of-sample performance versus model size planes. The BNNs predictively outperform the equivalent neural networks trained with a traditional backpropagation approach, and Bayesian marginalising/ensembling over architectures acts to further improve performance. 1: https://github.com/PolyChord/PolyChordLite 2: https://github.com/SuperKam91/bnn

Bayesian surrogate learning in dynamic simulator-based regression problems

The estimation of unknown values of parameters (or hidden variables, control variables) that characterise a physical system often relies on the comparison of measured data with synthetic data produced by some numerical simulator of the system as the parameter values are varied. This process often encounters two major difficulties: the generation of synthetic data for each considered set of parameter values can be computationally expensive if the system model is complicated; and the exploration of the parameter space can be inefficient and/or incomplete, a typical example being when the exploration becomes trapped in a local optimum of the objection function that characterises the mismatch between the measured and synthetic data. A method to address both these issues is presented, whereby: a surrogate model (or proxy), which emulates the computationally expensive system simulator, is constructed using deep recurrent networks (DRN); and a nested sampling (NS) algorithm is employed to perform efficient and robust exploration of the parameter space. The analysis is performed in a Bayesian context, in which the samples characterise the full joint posterior distribution of the parameters, from which parameter estimates and uncertainties are easily derived. The proposed approach is compared with conventional methods in some numerical examples, for which the results demonstrate that one can accelerate the parameter estimation process by at least an order of magnitude.