A comparison of Bayesian sampling algorithms for high-dimensional particle physics and cosmology applications

For several decades now, Bayesian inference techniques have been applied to theories of particle physics, cosmology and astrophysics to obtain the probability density functions of their free parameters. In this study, we review and compare a wide range of Markov Chain Monte Carlo (MCMC) and nested sampling techniques to determine their relative efficacy on functions that resemble those encountered most frequently in the particle astrophysics literature. Our first series of tests explores a series of high-dimensional analytic test functions that exemplify particular challenges, for example highly multimodal posteriors or posteriors with curving degeneracies. We then investigate two real physics examples, the first being a global fit of the $\Lambda$CDM model using cosmic microwave background data from the Planck experiment, and the second being a global fit of the Minimal Supersymmetric Standard Model using a wide variety of collider and astrophysics data. We show that several examples widely thought to be most easily solved using nested sampling approaches can in fact be more efficiently solved using modern MCMC algorithms, but the details of the implementation matter. Furthermore, we also provide a series of useful insights for practitioners of particle astrophysics and cosmology.

Improving Gradient-guided Nested Sampling for Posterior Inference

We present a performant, general-purpose gradient-guided nested sampling algorithm, ${\tt GGNS}$, combining the state of the art in differentiable programming, Hamiltonian slice sampling, clustering, mode separation, dynamic nested sampling, and parallelization. This unique combination allows ${\tt GGNS}$ to scale well with dimensionality and perform competitively on a variety of synthetic and real-world problems. We also show the potential of combining nested sampling with generative flow networks to obtain large amounts of high-quality samples from the posterior distribution. This combination leads to faster mode discovery and more accurate estimates of the partition function.

Kernel-, mean- and noise-marginalised Gaussian processes for exoplanet transits and $H_0$ inference

Using a fully Bayesian approach, Gaussian Process regression is extended to include marginalisation over the kernel choice and kernel hyperparameters. In addition, Bayesian model comparison via the evidence enables direct kernel comparison. The calculation of the joint posterior was implemented with a transdimensional sampler which simultaneously samples over the discrete kernel choice and their hyperparameters by embedding these in a higher-dimensional space, from which samples are taken using nested sampling. This method was explored on synthetic data from exoplanet transit light curve simulations. The true kernel was recovered in the low noise region while no kernel was preferred for larger noise. Furthermore, inference of the physical exoplanet hyperparameters was conducted. In the high noise region, either the bias in the posteriors was removed, the posteriors were broadened or the accuracy of the inference was increased. In addition, the uncertainty in mean function predictive distribution increased due to the uncertainty in the kernel choice. Subsequently, the method was extended to marginalisation over mean functions and noise models and applied to the inference of the present-day Hubble parameter, $H_0$, from real measurements of the Hubble parameter as a function of redshift, derived from the cosmologically model-independent cosmic chronometer and {\Lambda}CDM-dependent baryon acoustic oscillation observations. The inferred $H_0$ values from the cosmic chronometers, baryon acoustic oscillations and combined datasets are $H_0$ = 66$\pm$6 km/s/Mpc, $H_0$ = 67$\pm$10 km/s/Mpc and $H_0$ = 69$\pm$6 km/s/Mpc, respectively. The kernel posterior of the cosmic chronometers dataset prefers a non-stationary linear kernel. Finally, the datasets are shown to be not in tension with ln(R)=12.17$\pm$0.02.

Piecewise Normalizing Flows

Normalizing flows are an established approach for modelling complex probability densities through invertible transformations from a base distribution. However, the accuracy with which the target distribution can be captured by the normalizing flow is strongly influenced by the topology of the base distribution. A mismatch between the topology of the target and the base can result in a poor performance, as is the case for multi-modal problems. A number of different works have attempted to modify the topology of the base distribution to better match the target, either through the use of Gaussian Mixture Models [Izmailov et al., 2020, Ardizzone et al., 2020, Hagemann and Neumayer, 2021] or learned accept/reject sampling [Stimper et al., 2022]. We introduce piecewise normalizing flows which divide the target distribution into clusters, with topologies that better match the standard normal base distribution, and train a series of flows to model complex multi-modal targets. The piecewise nature of the flows can be exploited to significantly reduce the computational cost of training through parallelization. We demonstrate the performance of the piecewise flows using standard benchmarks and compare the accuracy of the flows to the approach taken in Stimper et al., 2022 for modelling multi-modal distributions.

Split personalities in Bayesian Neural Networks: the case for full marginalisation

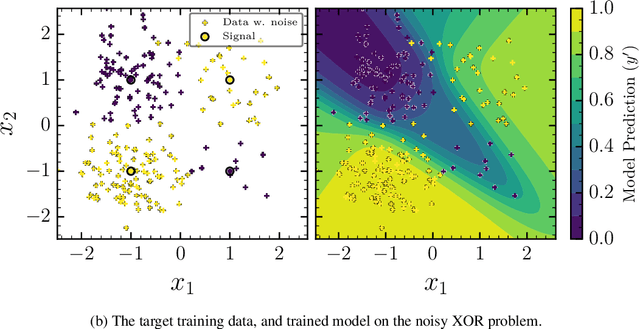
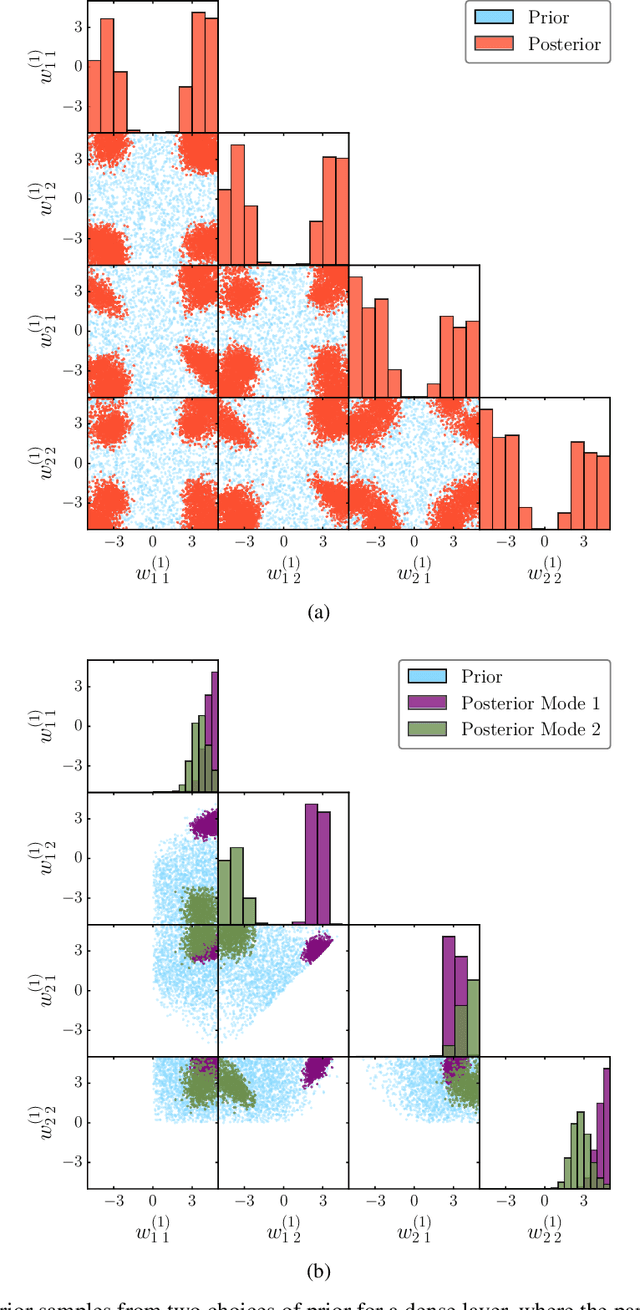
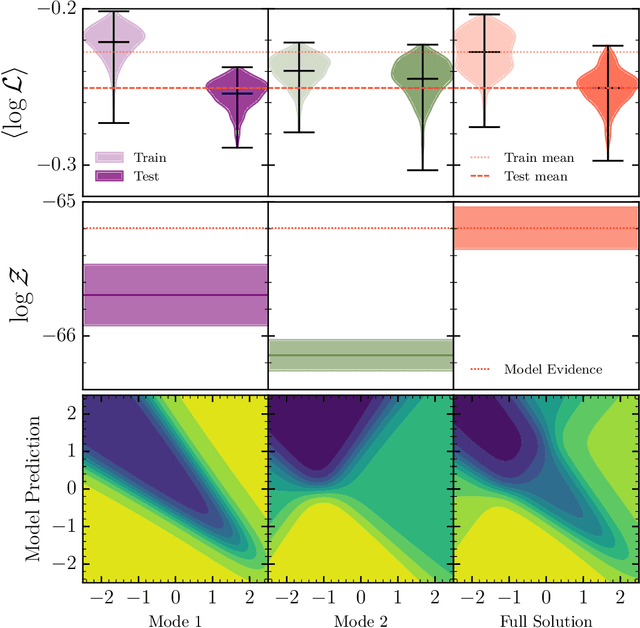
The true posterior distribution of a Bayesian neural network is massively multimodal. Whilst most of these modes are functionally equivalent, we demonstrate that there remains a level of real multimodality that manifests in even the simplest neural network setups. It is only by fully marginalising over all posterior modes, using appropriate Bayesian sampling tools, that we can capture the split personalities of the network. The ability of a network trained in this manner to reason between multiple candidate solutions dramatically improves the generalisability of the model, a feature we contend is not consistently captured by alternative approaches to the training of Bayesian neural networks. We provide a concise minimal example of this, which can provide lessons and a future path forward for correctly utilising the explainability and interpretability of Bayesian neural networks.

Nested sampling with any prior you like

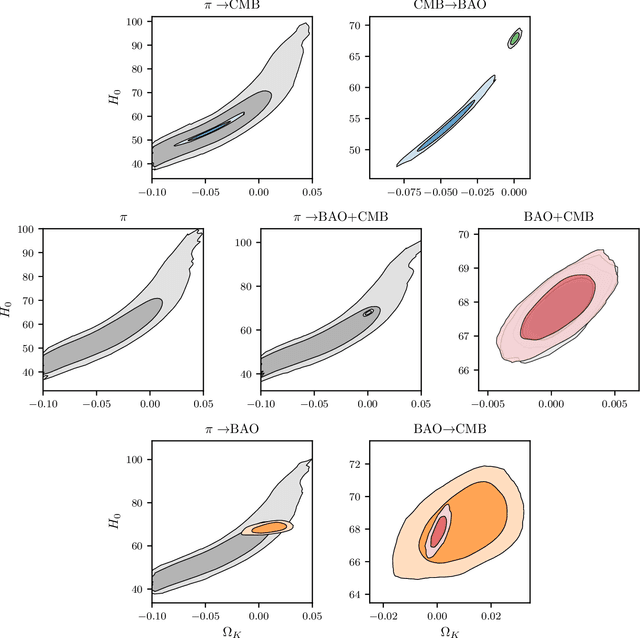
Nested sampling is an important tool for conducting Bayesian analysis in Astronomy and other fields, both for sampling complicated posterior distributions for parameter inference, and for computing marginal likelihoods for model comparison. One technical obstacle to using nested sampling in practice is the requirement (for most common implementations) that prior distributions be provided in the form of transformations from the unit hyper-cube to the target prior density. For many applications - particularly when using the posterior from one experiment as the prior for another - such a transformation is not readily available. In this letter we show that parametric bijectors trained on samples from a desired prior density provide a general-purpose method for constructing transformations from the uniform base density to a target prior, enabling the practical use of nested sampling under arbitrary priors. We demonstrate the use of trained bijectors in conjunction with nested sampling on a number of examples from cosmology.

Compromise-free Bayesian neural networks

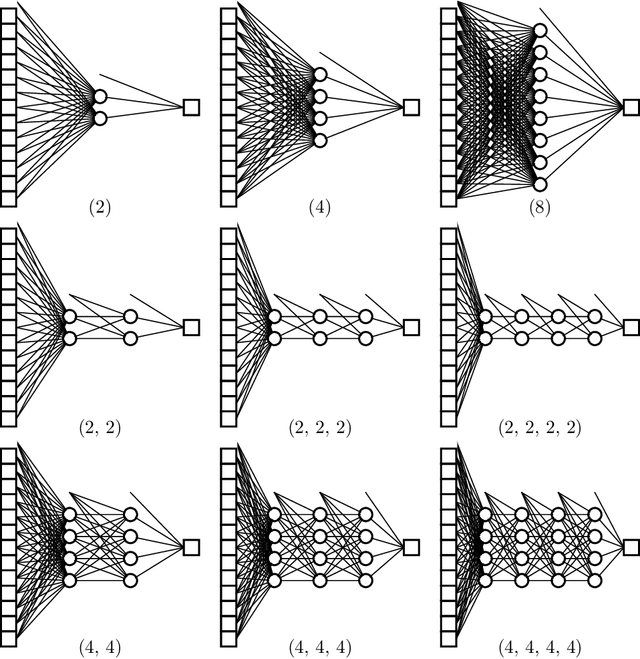
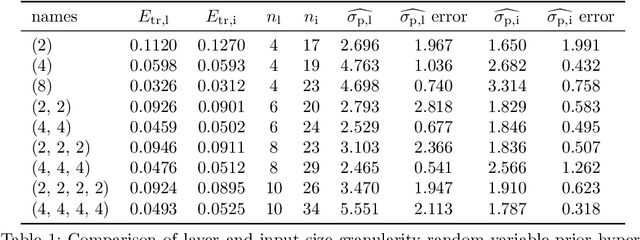
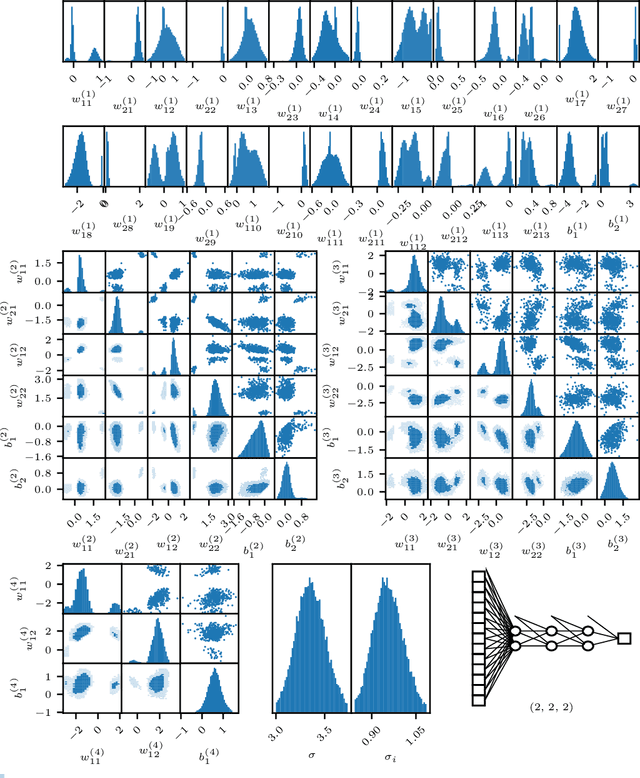
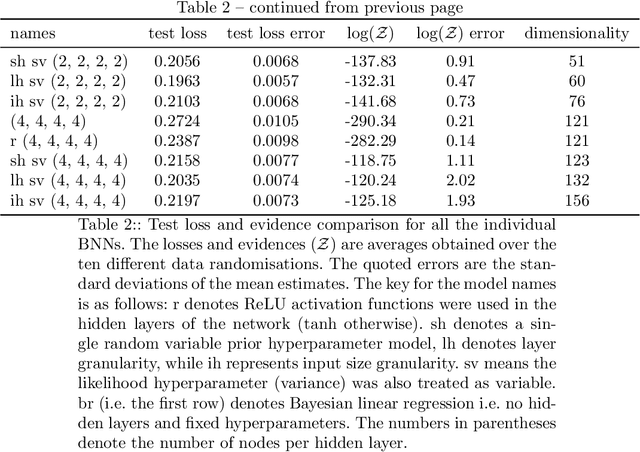
We conduct a thorough analysis of the relationship between the out-of-sample performance and the Bayesian evidence of Bayesian neural networks (BNNs) using the Boston housing dataset, as well as looking at the performance of ensembles of BNNs. We numerically sample without compromise the full network posterior and obtain estimates of the Bayesian evidence using the publicly available version of the nested sampling algorithm PolyChord$^1$ (Handley et al., 2015a,b), considering network models with up to 156 trainable parameters$^2$ (Javid and Handley, 2020). The networks have between zero and four hidden layers, either $\tanh$ or ReLU activation functions, and with and without hierarchical priors (MacKay, 1992c; Neal, 2012). The ensembles of BNNs are obtained by determining the posterior distribution over networks, from the posterior samples of individual BNNs re-weighted by the associated Bayesian evidence values. From the out-of-sample performance of the BNNs with ReLU activations, it is clear that they outperform BNNs of the same architecture with tanh activations, and evidence values corresponding to the former reflect this in their relatively high values. Looking at the models with hierarchical priors, there is a good correlation between out-of-sample performance and evidence, as was found in MacKay (1992c), as well as a remarkable symmetry between the evidence versus model size and out-of-sample performance versus model size planes. The BNNs predictively outperform the equivalent neural networks trained with a traditional backpropagation approach, and Bayesian marginalising/ensembling over architectures acts to further improve performance. 1: https://github.com/PolyChord/PolyChordLite 2: https://github.com/SuperKam91/bnn

Bayesian sparse reconstruction: a brute-force approach to astronomical imaging and machine learning

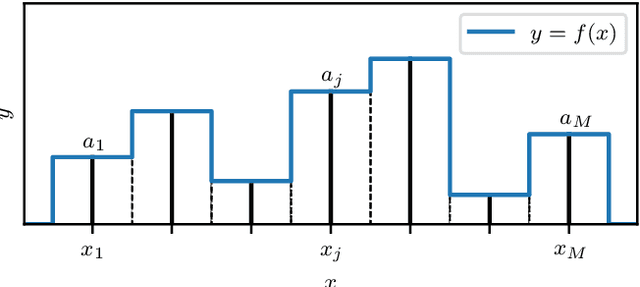
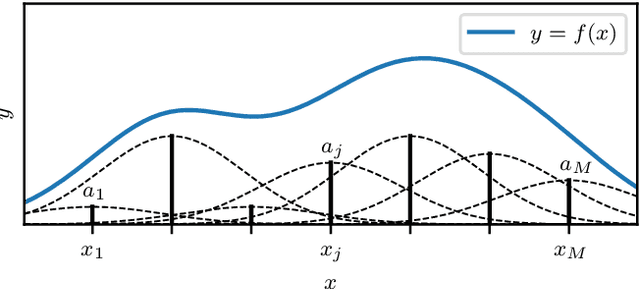
We present a principled Bayesian framework for signal reconstruction, in which the signal is modelled by basis functions whose number (and form, if required) is determined by the data themselves. This approach is based on a Bayesian interpretation of conventional sparse reconstruction and regularisation techniques, in which sparsity is imposed through priors via Bayesian model selection. We demonstrate our method for noisy 1- and 2-dimensional signals, including astronomical images. Furthermore, by using a product-space approach, the number and type of basis functions can be treated as integer parameters and their posterior distributions sampled directly. We show that order-of-magnitude increases in computational efficiency are possible from this technique compared to calculating the Bayesian evidences separately, and that further computational gains are possible using it in combination with dynamic nested sampling. Our approach can be readily applied to neural networks, where it allows the network architecture to be determined by the data in a principled Bayesian manner by treating the number of nodes and hidden layers as parameters.