Scaling-laws for Large Time-series Models

Scaling laws for large language models (LLMs) have provided useful guidance on how to train ever larger models for predictable performance gains. Time series forecasting shares a similar sequential structure to language, and is amenable to large-scale transformer architectures. Here we show that foundational decoder-only time series transformer models exhibit analogous scaling-behavior to LLMs, while architectural details (aspect ratio and number of heads) have a minimal effect over broad ranges. We assemble a large corpus of heterogenous time series data on which to train, and establish, for the first time, power-law scaling relations with respect to parameter count, dataset size, and training compute, spanning five orders of magnitude.

Optimal simulation-based Bayesian decisions

We present a framework for the efficient computation of optimal Bayesian decisions under intractable likelihoods, by learning a surrogate model for the expected utility (or its distribution) as a function of the action and data spaces. We leverage recent advances in simulation-based inference and Bayesian optimization to develop active learning schemes to choose where in parameter and action spaces to simulate. This allows us to learn the optimal action in as few simulations as possible. The resulting framework is extremely simulation efficient, typically requiring fewer model calls than the associated posterior inference task alone, and a factor of $100-1000$ more efficient than Monte-Carlo based methods. Our framework opens up new capabilities for performing Bayesian decision making, particularly in the previously challenging regime where likelihoods are intractable, and simulations expensive.

Fishnets: Information-Optimal, Scalable Aggregation for Sets and Graphs

Set-based learning is an essential component of modern deep learning and network science. Graph Neural Networks (GNNs) and their edge-free counterparts Deepsets have proven remarkably useful on ragged and topologically challenging datasets. The key to learning informative embeddings for set members is a specified aggregation function, usually a sum, max, or mean. We propose Fishnets, an aggregation strategy for learning information-optimal embeddings for sets of data for both Bayesian inference and graph aggregation. We demonstrate that i) Fishnets neural summaries can be scaled optimally to an arbitrary number of data objects, ii) Fishnets aggregations are robust to changes in data distribution, unlike standard deepsets, iii) Fishnets saturate Bayesian information content and extend to regimes where MCMC techniques fail and iv) Fishnets can be used as a drop-in aggregation scheme within GNNs. We show that by adopting a Fishnets aggregation scheme for message passing, GNNs can achieve state-of-the-art performance versus architecture size on ogbn-protein data over existing benchmarks with a fraction of learnable parameters and faster training time.

Removing the fat from your posterior samples with margarine

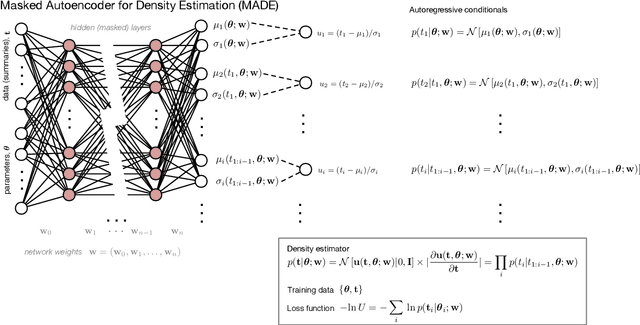
Bayesian workflows often require the introduction of nuisance parameters, yet for core science modelling one needs access to a marginal posterior density. In this work we use masked autoregressive flows and kernel density estimators to encapsulate the marginal posterior, allowing us to compute marginal Kullback-Leibler divergences and marginal Bayesian model dimensionalities in addition to generating samples and computing marginal log probabilities. We demonstrate this in application to topical cosmological examples of the Dark Energy Survey, and global 21cm signal experiments. In addition to the computation of marginal Bayesian statistics, this work is important for further applications in Bayesian experimental design, complex prior modelling and likelihood emulation. This technique is made publicly available in the pip-installable code margarine.

Nested sampling with any prior you like

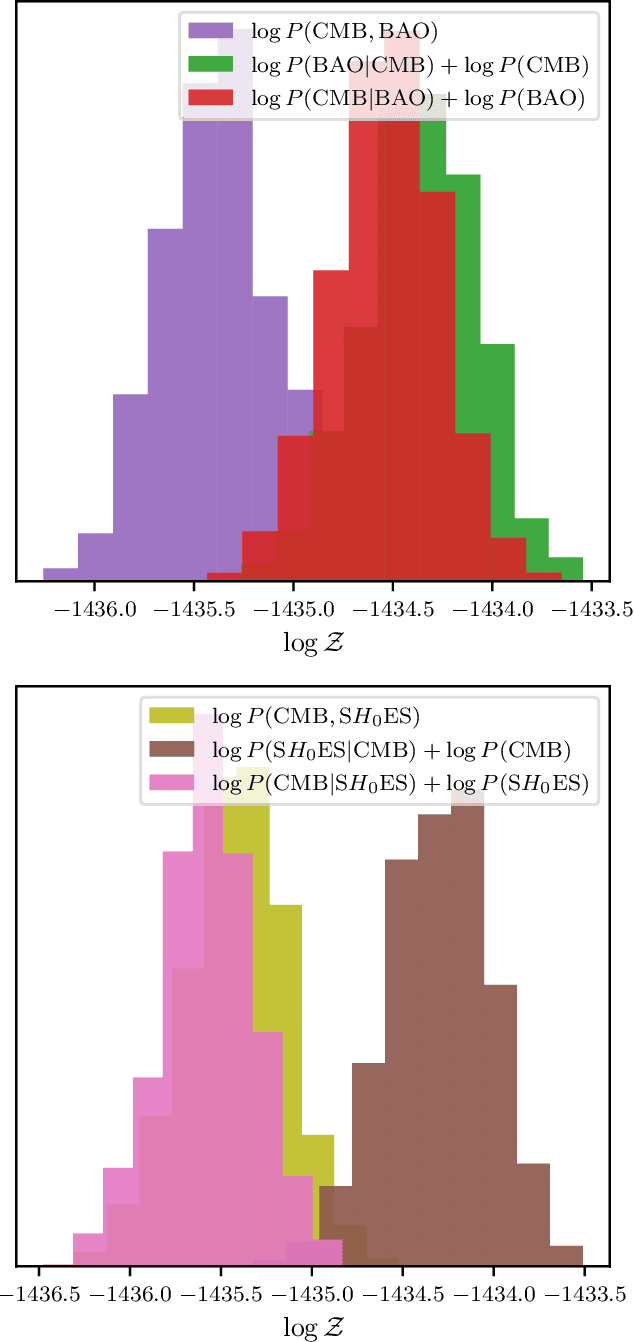
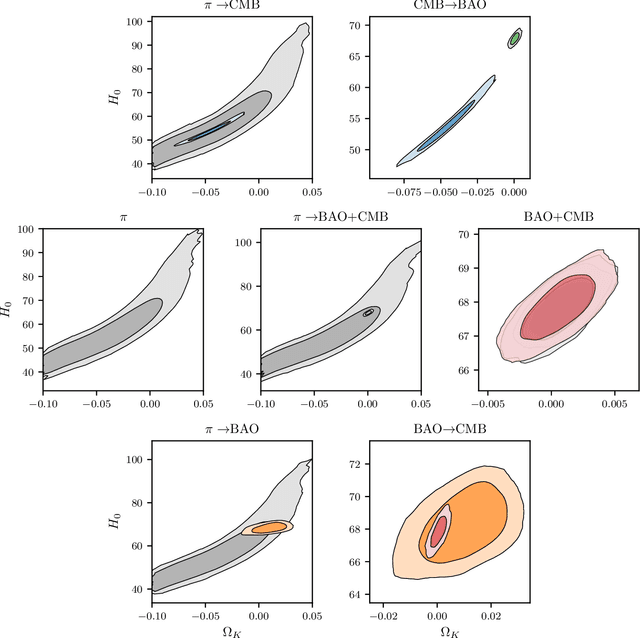
Nested sampling is an important tool for conducting Bayesian analysis in Astronomy and other fields, both for sampling complicated posterior distributions for parameter inference, and for computing marginal likelihoods for model comparison. One technical obstacle to using nested sampling in practice is the requirement (for most common implementations) that prior distributions be provided in the form of transformations from the unit hyper-cube to the target prior density. For many applications - particularly when using the posterior from one experiment as the prior for another - such a transformation is not readily available. In this letter we show that parametric bijectors trained on samples from a desired prior density provide a general-purpose method for constructing transformations from the uniform base density to a target prior, enabling the practical use of nested sampling under arbitrary priors. We demonstrate the use of trained bijectors in conjunction with nested sampling on a number of examples from cosmology.

Fast likelihood-free cosmology with neural density estimators and active learning

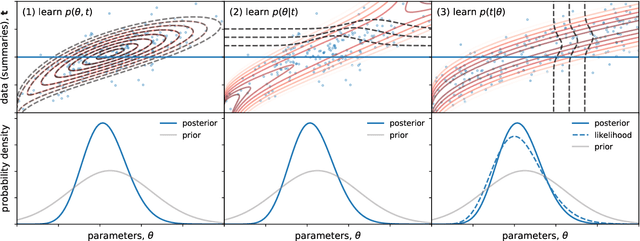
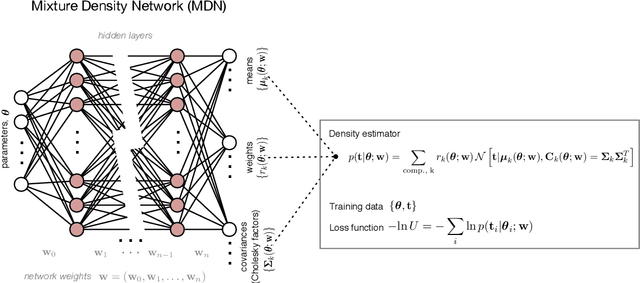
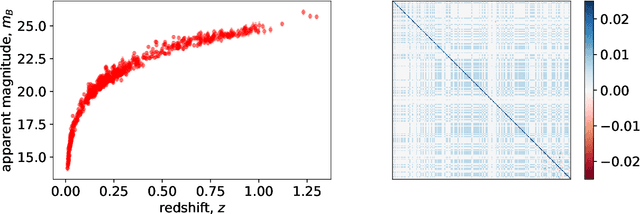
Likelihood-free inference provides a framework for performing rigorous Bayesian inference using only forward simulations, properly accounting for all physical and observational effects that can be successfully included in the simulations. The key challenge for likelihood-free applications in cosmology, where simulation is typically expensive, is developing methods that can achieve high-fidelity posterior inference with as few simulations as possible. Density-estimation likelihood-free inference (DELFI) methods turn inference into a density estimation task on a set of simulated data-parameter pairs, and give orders of magnitude improvements over traditional Approximate Bayesian Computation approaches to likelihood-free inference. In this paper we use neural density estimators (NDEs) to learn the likelihood function from a set of simulated datasets, with active learning to adaptively acquire simulations in the most relevant regions of parameter space on-the-fly. We demonstrate the approach on a number of cosmological case studies, showing that for typical problems high-fidelity posterior inference can be achieved with just $\mathcal{O}(10^3)$ simulations or fewer. In addition to enabling efficient simulation-based inference, for simple problems where the form of the likelihood is known, DELFI offers a fast alternative to MCMC sampling, giving orders of magnitude speed-up in some cases. Finally, we introduce \textsc{pydelfi} -- a flexible public implementation of DELFI with NDEs and active learning -- available at \url{https://github.com/justinalsing/pydelfi}.