Hybrid summary statistics: neural weak lensing inference beyond the power spectrum

In inference problems, we often have domain knowledge which allows us to define summary statistics that capture most of the information content in a dataset. In this paper, we present a hybrid approach, where such physics-based summaries are augmented by a set of compressed neural summary statistics that are optimised to extract the extra information that is not captured by the predefined summaries. The resulting statistics are very powerful inputs to simulation-based or implicit inference of model parameters. We apply this generalisation of Information Maximising Neural Networks (IMNNs) to parameter constraints from tomographic weak gravitational lensing convergence maps to find summary statistics that are explicitly optimised to complement angular power spectrum estimates. We study several dark matter simulation resolutions in low- and high-noise regimes. We show that i) the information-update formalism extracts at least $3\times$ and up to $8\times$ as much information as the angular power spectrum in all noise regimes, ii) the network summaries are highly complementary to existing 2-point summaries, and iii) our formalism allows for networks with smaller, physically-informed architectures to match much larger regression networks with far fewer simulations needed to obtain asymptotically optimal inference.

The Cosmic Graph: Optimal Information Extraction from Large-Scale Structure using Catalogues

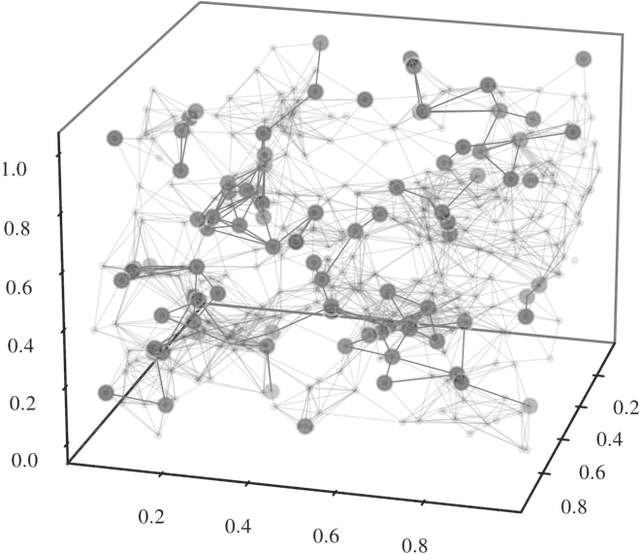
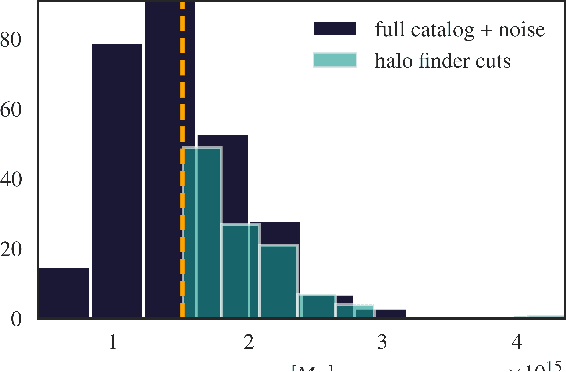
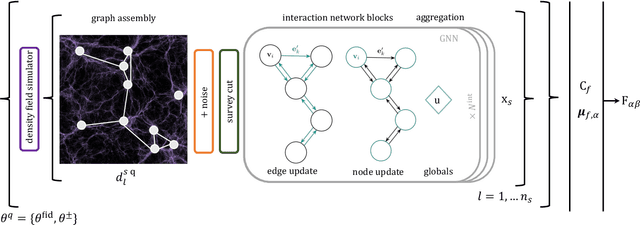
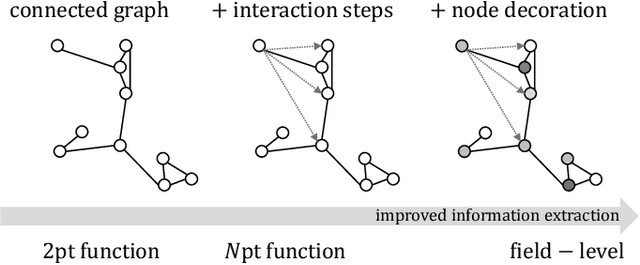
We present an implicit likelihood approach to quantifying cosmological information over discrete catalogue data, assembled as graphs. To do so, we explore cosmological inference using mock dark matter halo catalogues. We employ Information Maximising Neural Networks (IMNNs) to quantify Fisher information extraction as a function of graph representation. We a) demonstrate the high sensitivity of modular graph structure to the underlying cosmology in the noise-free limit, b) show that networks automatically combine mass and clustering information through comparisons to traditional statistics, c) demonstrate that graph neural networks can still extract information when catalogues are subject to noisy survey cuts, and d) illustrate how nonlinear IMNN summaries can be used as asymptotically optimal compressed statistics for Bayesian implicit likelihood inference. We reduce the area of joint $\Omega_m, \sigma_8$ parameter constraints with small ($\sim$100 object) halo catalogues by a factor of 42 over the two-point correlation function, and demonstrate that the networks automatically combine mass and clustering information. This work utilises a new IMNN implementation over graph data in Jax, which can take advantage of either numerical or auto-differentiability. We also show that graph IMNNs successfully compress simulations far from the fiducial model at which the network is fitted, indicating a promising alternative to $n$-point statistics in catalogue-based analyses.

Bayesian Neural Networks

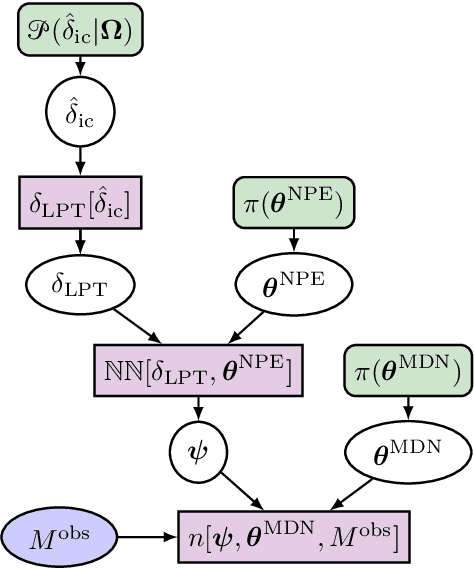
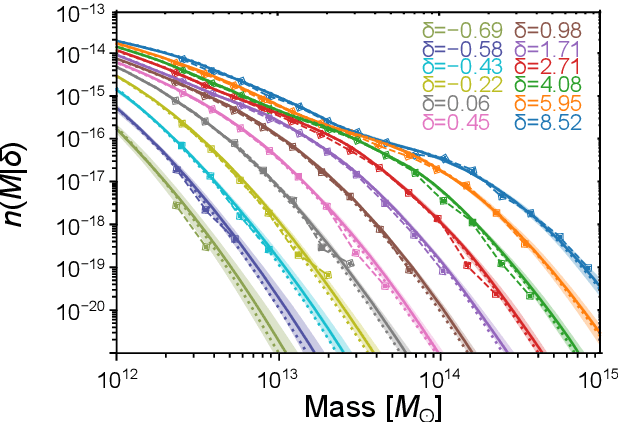
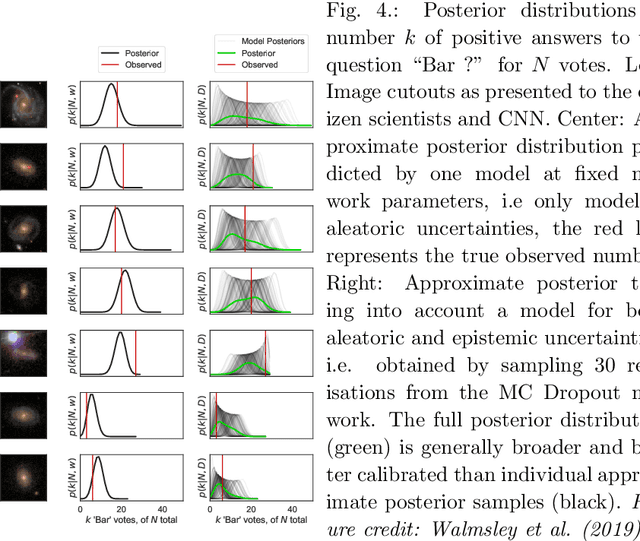
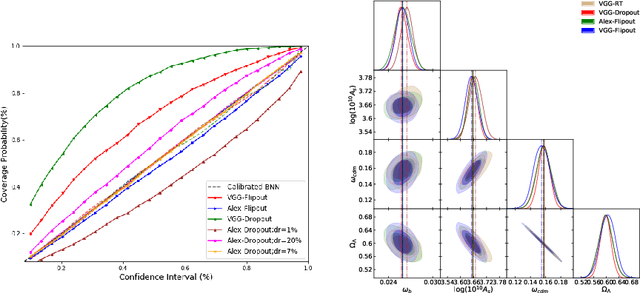
In recent times, neural networks have become a powerful tool for the analysis of complex and abstract data models. However, their introduction intrinsically increases our uncertainty about which features of the analysis are model-related and which are due to the neural network. This means that predictions by neural networks have biases which cannot be trivially distinguished from being due to the true nature of the creation and observation of data or not. In order to attempt to address such issues we discuss Bayesian neural networks: neural networks where the uncertainty due to the network can be characterised. In particular, we present the Bayesian statistical framework which allows us to categorise uncertainty in terms of the ingrained randomness of observing certain data and the uncertainty from our lack of knowledge about how data can be created and observed. In presenting such techniques we show how errors in prediction by neural networks can be obtained in principle, and provide the two favoured methods for characterising these errors. We will also describe how both of these methods have substantial pitfalls when put into practice, highlighting the need for other statistical techniques to truly be able to do inference when using neural networks.

Fast likelihood-free cosmology with neural density estimators and active learning

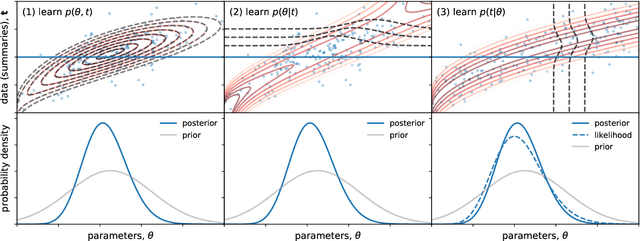
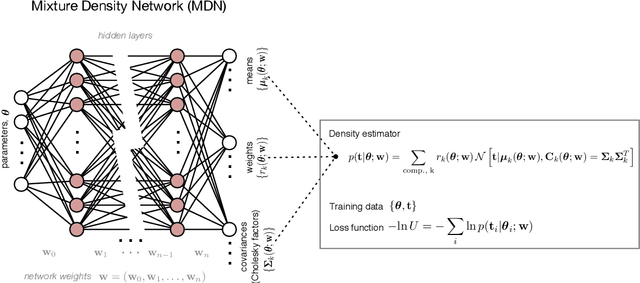
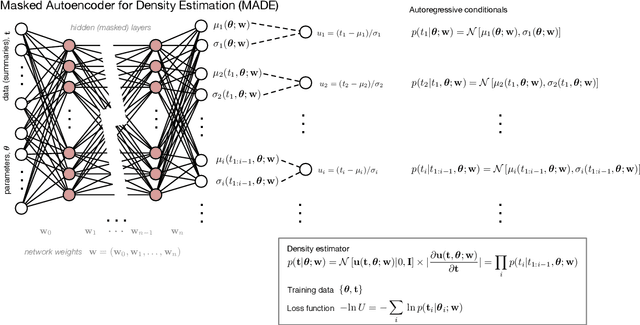
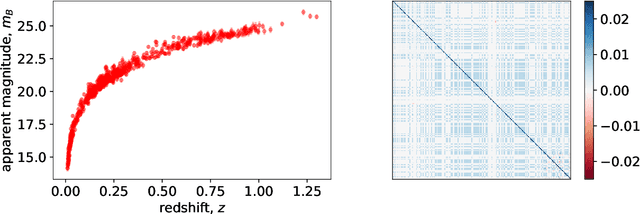
Likelihood-free inference provides a framework for performing rigorous Bayesian inference using only forward simulations, properly accounting for all physical and observational effects that can be successfully included in the simulations. The key challenge for likelihood-free applications in cosmology, where simulation is typically expensive, is developing methods that can achieve high-fidelity posterior inference with as few simulations as possible. Density-estimation likelihood-free inference (DELFI) methods turn inference into a density estimation task on a set of simulated data-parameter pairs, and give orders of magnitude improvements over traditional Approximate Bayesian Computation approaches to likelihood-free inference. In this paper we use neural density estimators (NDEs) to learn the likelihood function from a set of simulated datasets, with active learning to adaptively acquire simulations in the most relevant regions of parameter space on-the-fly. We demonstrate the approach on a number of cosmological case studies, showing that for typical problems high-fidelity posterior inference can be achieved with just $\mathcal{O}(10^3)$ simulations or fewer. In addition to enabling efficient simulation-based inference, for simple problems where the form of the likelihood is known, DELFI offers a fast alternative to MCMC sampling, giving orders of magnitude speed-up in some cases. Finally, we introduce \textsc{pydelfi} -- a flexible public implementation of DELFI with NDEs and active learning -- available at \url{https://github.com/justinalsing/pydelfi}.

Deep Recurrent Neural Networks for Supernovae Classification

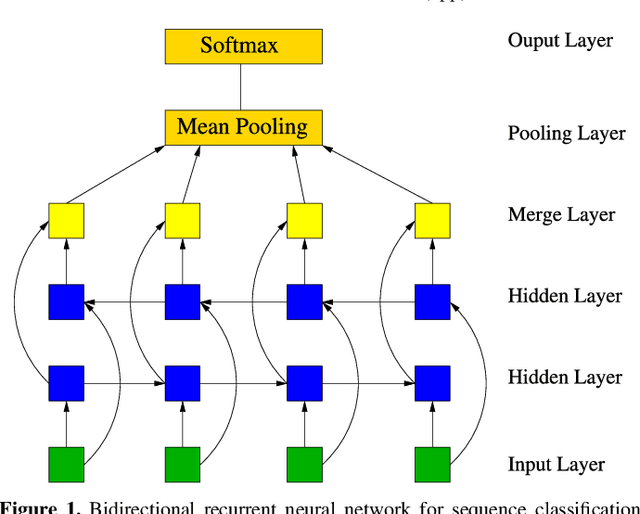
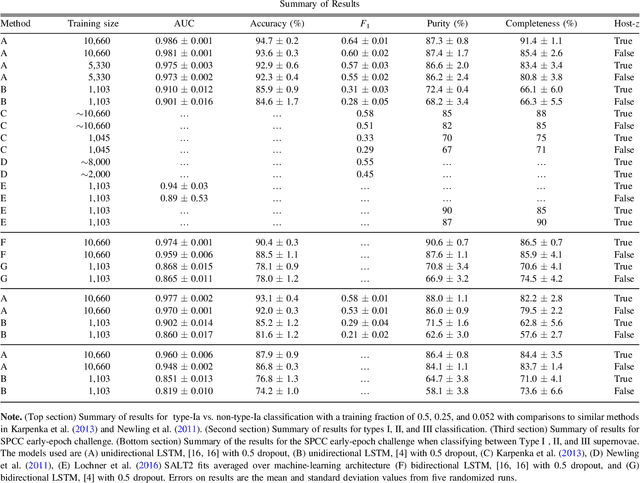
We apply deep recurrent neural networks, which are capable of learning complex sequential information, to classify supernovae\footnote{Code available at \href{https://github.com/adammoss/supernovae}{https://github.com/adammoss/supernovae}}. The observational time and filter fluxes are used as inputs to the network, but since the inputs are agnostic additional data such as host galaxy information can also be included. Using the Supernovae Photometric Classification Challenge (SPCC) data, we find that deep networks are capable of learning about light curves, however the performance of the network is highly sensitive to the amount of training data. For a training size of 50\% of the representational SPCC dataset (around $10^4$ supernovae) we obtain a type-Ia vs. non-type-Ia classification accuracy of 94.7\%, an area under the Receiver Operating Characteristic curve AUC of 0.986 and a SPCC figure-of-merit $F_1=0.64$. When using only the data for the early-epoch challenge defined by the SPCC we achieve a classification accuracy of 93.1\%, AUC of 0.977 and $F_1=0.58$, results almost as good as with the whole light-curve. By employing bidirectional neural networks we can acquire impressive classification results between supernovae types -I,~-II and~-III at an accuracy of 90.4\% and AUC of 0.974. We also apply a pre-trained model to obtain classification probabilities as a function of time, and show it can give early indications of supernovae type. Our method is competitive with existing algorithms and has applications for future large-scale photometric surveys.