Towards Mitigating Systematics in Large-Scale Surveys via Few-Shot Optimal Transport-Based Feature Alignment

Systematics contaminate observables, leading to distribution shifts relative to theoretically simulated signals-posing a major challenge for using pre-trained models to label such observables. Since systematics are often poorly understood and difficult to model, removing them directly and entirely may not be feasible. To address this challenge, we propose a novel method that aligns learned features between in-distribution (ID) and out-of-distribution (OOD) samples by optimizing a feature-alignment loss on the representations extracted from a pre-trained ID model. We first experimentally validate the method on the MNIST dataset using possible alignment losses, including mean squared error and optimal transport, and subsequently apply it to large-scale maps of neutral hydrogen. Our results show that optimal transport is particularly effective at aligning OOD features when parity between ID and OOD samples is unknown, even with limited data-mimicking real-world conditions in extracting information from large-scale surveys. Our code is available at https://github.com/sultan-hassan/feature-alignment-for-OOD-generalization.

Galactification: painting galaxies onto dark matter only simulations using a transformer-based model

Connecting the formation and evolution of galaxies to the large-scale structure is crucial for interpreting cosmological observations. While hydrodynamical simulations accurately model the correlated properties of galaxies, they are computationally prohibitive to run over volumes that match modern surveys. We address this by developing a framework to rapidly generate mock galaxy catalogs conditioned on inexpensive dark-matter-only simulations. We present a multi-modal, transformer-based model that takes 3D dark matter density and velocity fields as input, and outputs a corresponding point cloud of galaxies with their physical properties. We demonstrate that our trained model faithfully reproduces a variety of galaxy summary statistics and correctly captures their variation with changes in the underlying cosmological and astrophysical parameters, making it the first accelerated forward model to capture all the relevant galaxy properties, their full spatial distribution, and their conditional dependencies in hydrosimulations.

syren-new: Precise formulae for the linear and nonlinear matter power spectra with massive neutrinos and dynamical dark energy

Current and future large scale structure surveys aim to constrain the neutrino mass and the equation of state of dark energy. We aim to construct accurate and interpretable symbolic approximations to the linear and nonlinear matter power spectra as a function of cosmological parameters in extended $\Lambda$CDM models which contain massive neutrinos and non-constant equations of state for dark energy. This constitutes an extension of the syren-halofit emulators to incorporate these two effects, which we call syren-new (SYmbolic-Regression-ENhanced power spectrum emulator with NEutrinos and $W_0-w_a$). We also obtain a simple approximation to the derived parameter $\sigma_8$ as a function of the cosmological parameters for these models. Our results for the linear power spectrum are designed to emulate CLASS, whereas for the nonlinear case we aim to match the results of EuclidEmulator2. We compare our results to existing emulators and $N$-body simulations. Our analytic emulators for $\sigma_8$, the linear and nonlinear power spectra achieve root mean squared errors of 0.1%, 0.3% and 1.3%, respectively, across a wide range of cosmological parameters, redshifts and wavenumbers. We verify that emulator-related discrepancies are subdominant compared to observational errors and other modelling uncertainties when computing shear power spectra for LSST-like surveys. Our expressions have similar accuracy to existing (numerical) emulators, but are at least an order of magnitude faster, both on a CPU and GPU. Our work greatly improves the accuracy, speed and range of applicability of current symbolic approximations to the linear and nonlinear matter power spectra. We provide publicly available code for all symbolic approximations found.

Hybrid Summary Statistics

We present a way to capture high-information posteriors from training sets that are sparsely sampled over the parameter space for robust simulation-based inference. In physical inference problems, we can often apply domain knowledge to define traditional summary statistics to capture some of the information in a dataset. We show that augmenting these statistics with neural network outputs to maximise the mutual information improves information extraction compared to neural summaries alone or their concatenation to existing summaries and makes inference robust in settings with low training data. We introduce 1) two loss formalisms to achieve this and 2) apply the technique to two different cosmological datasets to extract non-Gaussian parameter information.

CHARM: Creating Halos with Auto-Regressive Multi-stage networks

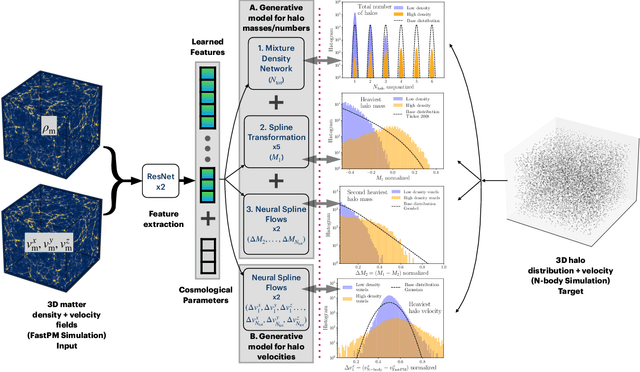
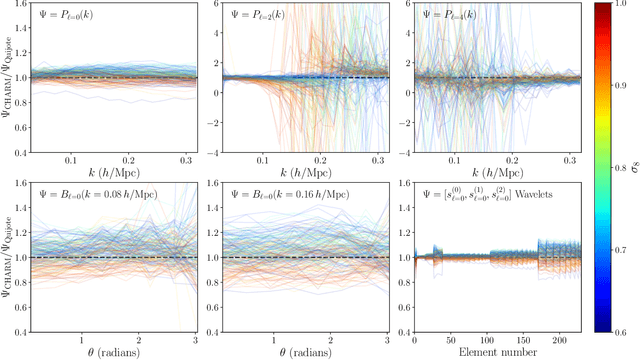
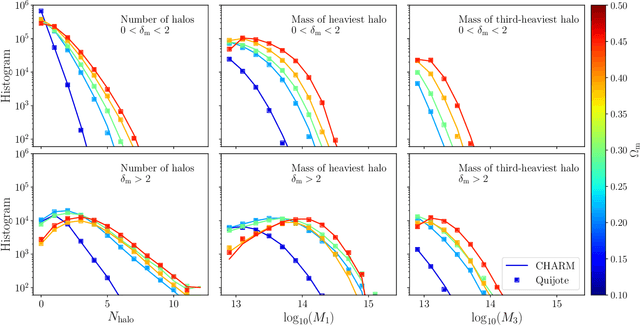
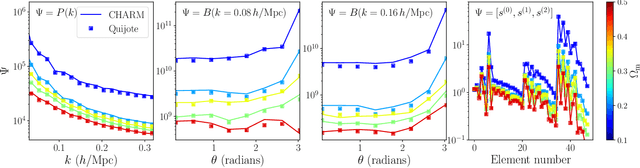
To maximize the amount of information extracted from cosmological datasets, simulations that accurately represent these observations are necessary. However, traditional simulations that evolve particles under gravity by estimating particle-particle interactions (N-body simulations) are computationally expensive and prohibitive to scale to the large volumes and resolutions necessary for the upcoming datasets. Moreover, modeling the distribution of galaxies typically involves identifying virialized dark matter halos, which is also a time- and memory-consuming process for large N-body simulations, further exacerbating the computational cost. In this study, we introduce CHARM, a novel method for creating mock halo catalogs by matching the spatial, mass, and velocity statistics of halos directly from the large-scale distribution of the dark matter density field. We develop multi-stage neural spline flow-based networks to learn this mapping at redshift z=0.5 directly with computationally cheaper low-resolution particle mesh simulations instead of relying on the high-resolution N-body simulations. We show that the mock halo catalogs and painted galaxy catalogs have the same statistical properties as obtained from $N$-body simulations in both real space and redshift space. Finally, we use these mock catalogs for cosmological inference using redshift-space galaxy power spectrum, bispectrum, and wavelet-based statistics using simulation-based inference, performing the first inference with accelerated forward model simulations and finding unbiased cosmological constraints with well-calibrated posteriors. The code was developed as part of the Simons Collaboration on Learning the Universe and is publicly available at \url{https://github.com/shivampcosmo/CHARM}.

Hybrid summary statistics: neural weak lensing inference beyond the power spectrum

In inference problems, we often have domain knowledge which allows us to define summary statistics that capture most of the information content in a dataset. In this paper, we present a hybrid approach, where such physics-based summaries are augmented by a set of compressed neural summary statistics that are optimised to extract the extra information that is not captured by the predefined summaries. The resulting statistics are very powerful inputs to simulation-based or implicit inference of model parameters. We apply this generalisation of Information Maximising Neural Networks (IMNNs) to parameter constraints from tomographic weak gravitational lensing convergence maps to find summary statistics that are explicitly optimised to complement angular power spectrum estimates. We study several dark matter simulation resolutions in low- and high-noise regimes. We show that i) the information-update formalism extracts at least $3\times$ and up to $8\times$ as much information as the angular power spectrum in all noise regimes, ii) the network summaries are highly complementary to existing 2-point summaries, and iii) our formalism allows for networks with smaller, physically-informed architectures to match much larger regression networks with far fewer simulations needed to obtain asymptotically optimal inference.

Scaling-laws for Large Time-series Models

Scaling laws for large language models (LLMs) have provided useful guidance on how to train ever larger models for predictable performance gains. Time series forecasting shares a similar sequential structure to language, and is amenable to large-scale transformer architectures. Here we show that foundational decoder-only time series transformer models exhibit analogous scaling-behavior to LLMs, while architectural details (aspect ratio and number of heads) have a minimal effect over broad ranges. We assemble a large corpus of heterogenous time series data on which to train, and establish, for the first time, power-law scaling relations with respect to parameter count, dataset size, and training compute, spanning five orders of magnitude.

syren-halofit: A fast, interpretable, high-precision formula for the $Λ$CDM nonlinear matter power spectrum

Rapid and accurate evaluation of the nonlinear matter power spectrum, $P(k)$, as a function of cosmological parameters and redshift is of fundamental importance in cosmology. Analytic approximations provide an interpretable solution, yet current approximations are neither fast nor accurate relative to black-box numerical emulators. We use symbolic regression to obtain simple analytic approximations to the nonlinear scale, $k_\sigma$, the effective spectral index, $n_{\rm eff}$, and the curvature, $C$, which are required for the halofit model. We then re-optimise the coefficients of halofit to fit a wide range of cosmologies and redshifts. We then again exploit symbolic regression to explore the space of analytic expressions to fit the residuals between $P(k)$ and the optimised predictions of halofit. All methods are validated against $N$-body simulations. Our symbolic expressions for $k_\sigma$, $n_{\rm eff}$ and $C$ have root mean squared fractional errors of 0.8%, 0.2% and 0.3%, respectively, for redshifts below 3 and a wide range of cosmologies. The re-optimised halofit parameters reduce the root mean squared fractional error from 3% to below 2% for wavenumbers $k=9\times10^{-3}-9 \, h{\rm Mpc^{-1}}$. We introduce syren-halofit (symbolic-regression-enhanced halofit), an extension to halofit containing a short symbolic correction which improves this error to 1%. Our method is 2350 and 3170 times faster than current halofit and hmcode implementations, respectively, and 2680 and 64 times faster than EuclidEmulator2 (which requires running class) and the BACCO emulator. We obtain comparable accuracy to EuclidEmulator2 and the BACCO emulator when tested on $N$-body simulations. Our work greatly increases the speed and accuracy of symbolic approximations to $P(k)$, making them significantly faster than their numerical counterparts without loss of accuracy.

A precise symbolic emulator of the linear matter power spectrum

Computing the matter power spectrum, $P(k)$, as a function of cosmological parameters can be prohibitively slow in cosmological analyses, hence emulating this calculation is desirable. Previous analytic approximations are insufficiently accurate for modern applications, so black-box, uninterpretable emulators are often used. We utilise an efficient genetic programming based symbolic regression framework to explore the space of potential mathematical expressions which can approximate the power spectrum and $\sigma_8$. We learn the ratio between an existing low-accuracy fitting function for $P(k)$ and that obtained by solving the Boltzmann equations and thus still incorporate the physics which motivated this earlier approximation. We obtain an analytic approximation to the linear power spectrum with a root mean squared fractional error of 0.2% between $k = 9\times10^{-3} - 9 \, h{\rm \, Mpc^{-1}}$ and across a wide range of cosmological parameters, and we provide physical interpretations for various terms in the expression. We also provide a simple analytic approximation for $\sigma_8$ with a similar accuracy, with a root mean squared fractional error of just 0.4% when evaluated across the same range of cosmologies. This function is easily invertible to obtain $A_{\rm s}$ as a function of $\sigma_8$ and the other cosmological parameters, if preferred. It is possible to obtain symbolic approximations to a seemingly complex function at a precision required for current and future cosmological analyses without resorting to deep-learning techniques, thus avoiding their black-box nature and large number of parameters. Our emulator will be usable long after the codes on which numerical approximations are built become outdated.

Fishnets: Information-Optimal, Scalable Aggregation for Sets and Graphs

Set-based learning is an essential component of modern deep learning and network science. Graph Neural Networks (GNNs) and their edge-free counterparts Deepsets have proven remarkably useful on ragged and topologically challenging datasets. The key to learning informative embeddings for set members is a specified aggregation function, usually a sum, max, or mean. We propose Fishnets, an aggregation strategy for learning information-optimal embeddings for sets of data for both Bayesian inference and graph aggregation. We demonstrate that i) Fishnets neural summaries can be scaled optimally to an arbitrary number of data objects, ii) Fishnets aggregations are robust to changes in data distribution, unlike standard deepsets, iii) Fishnets saturate Bayesian information content and extend to regimes where MCMC techniques fail and iv) Fishnets can be used as a drop-in aggregation scheme within GNNs. We show that by adopting a Fishnets aggregation scheme for message passing, GNNs can achieve state-of-the-art performance versus architecture size on ogbn-protein data over existing benchmarks with a fraction of learnable parameters and faster training time.