$\mathtt{emuflow}$: Normalising Flows for Joint Cosmological Analysis

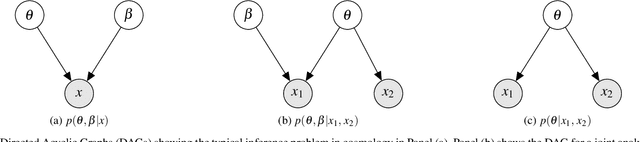
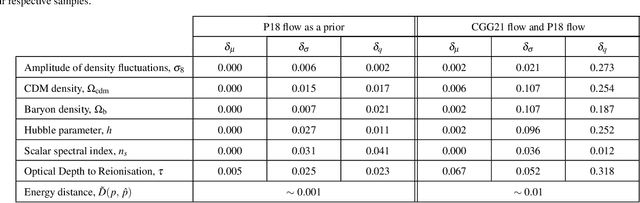
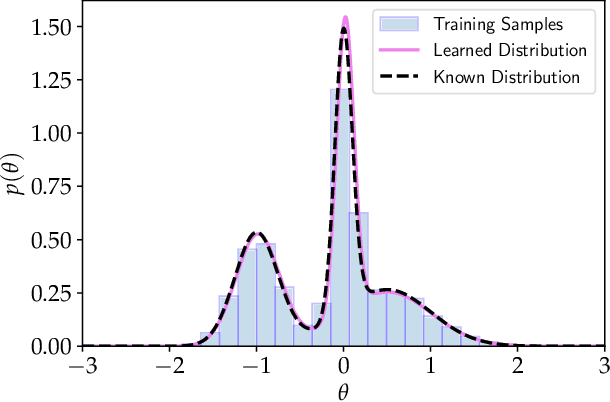
Given the growth in the variety and precision of astronomical datasets of interest for cosmology, the best cosmological constraints are invariably obtained by combining data from different experiments. At the likelihood level, one complication in doing so is the need to marginalise over large-dimensional parameter models describing the data of each experiment. These include both the relatively small number of cosmological parameters of interest and a large number of "nuisance" parameters. Sampling over the joint parameter space for multiple experiments can thus become a very computationally expensive operation. This can be significantly simplified if one could sample directly from the marginal cosmological posterior distribution of preceding experiments, depending only on the common set of cosmological parameters. In this paper, we show that this can be achieved by emulating marginal posterior distributions via normalising flows. The resulting trained normalising flow models can be used to efficiently combine cosmological constraints from independent datasets without increasing the dimensionality of the parameter space under study. We show that the method is able to accurately describe the posterior distribution of real cosmological datasets, as well as the joint distribution of different datasets, even when significant tension exists between experiments. The resulting joint constraints can be obtained in a fraction of the time it would take to combine the same datasets at the level of their likelihoods. We construct normalising flow models for a set of public cosmological datasets of general interests and make them available, together with the software used to train them, and to exploit them in cosmological parameter inference.

A precise symbolic emulator of the linear matter power spectrum

Computing the matter power spectrum, $P(k)$, as a function of cosmological parameters can be prohibitively slow in cosmological analyses, hence emulating this calculation is desirable. Previous analytic approximations are insufficiently accurate for modern applications, so black-box, uninterpretable emulators are often used. We utilise an efficient genetic programming based symbolic regression framework to explore the space of potential mathematical expressions which can approximate the power spectrum and $\sigma_8$. We learn the ratio between an existing low-accuracy fitting function for $P(k)$ and that obtained by solving the Boltzmann equations and thus still incorporate the physics which motivated this earlier approximation. We obtain an analytic approximation to the linear power spectrum with a root mean squared fractional error of 0.2% between $k = 9\times10^{-3} - 9 \, h{\rm \, Mpc^{-1}}$ and across a wide range of cosmological parameters, and we provide physical interpretations for various terms in the expression. We also provide a simple analytic approximation for $\sigma_8$ with a similar accuracy, with a root mean squared fractional error of just 0.4% when evaluated across the same range of cosmologies. This function is easily invertible to obtain $A_{\rm s}$ as a function of $\sigma_8$ and the other cosmological parameters, if preferred. It is possible to obtain symbolic approximations to a seemingly complex function at a precision required for current and future cosmological analyses without resorting to deep-learning techniques, thus avoiding their black-box nature and large number of parameters. Our emulator will be usable long after the codes on which numerical approximations are built become outdated.