The Inefficiency of Genetic Programming for Symbolic Regression -- Extended Version

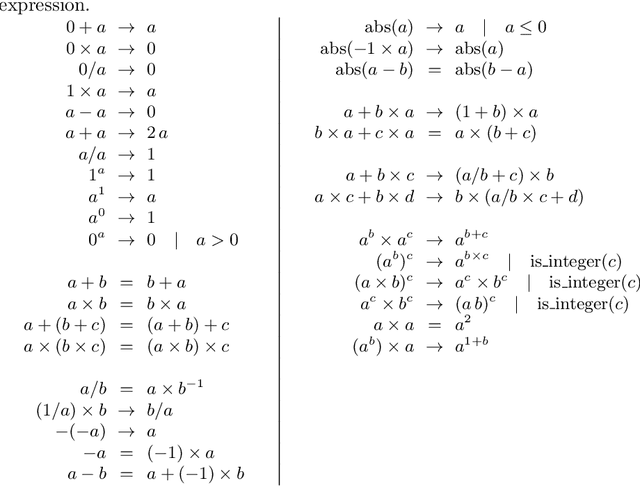
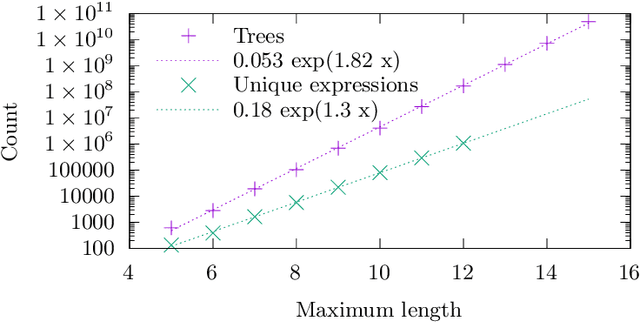
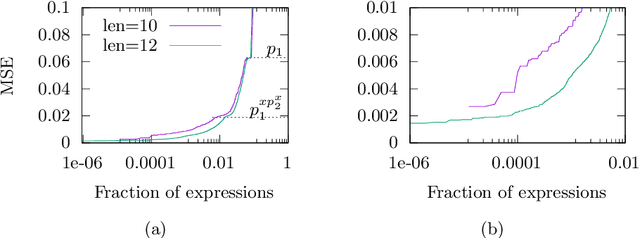
We analyse the search behaviour of genetic programming for symbolic regression in practically relevant but limited settings, allowing exhaustive enumeration of all solutions. This enables us to quantify the success probability of finding the best possible expressions, and to compare the search efficiency of genetic programming to random search in the space of semantically unique expressions. This analysis is made possible by improved algorithms for equality saturation, which we use to improve the Exhaustive Symbolic Regression algorithm; this produces the set of semantically unique expression structures, orders of magnitude smaller than the full symbolic regression search space. We compare the efficiency of random search in the set of unique expressions and genetic programming. For our experiments we use two real-world datasets where symbolic regression has been used to produce well-fitting univariate expressions: the Nikuradse dataset of flow in rough pipes and the Radial Acceleration Relation of galaxy dynamics. The results show that genetic programming in such limited settings explores only a small fraction of all unique expressions, and evaluates expressions repeatedly that are congruent to already visited expressions.

A precise symbolic emulator of the linear matter power spectrum

Computing the matter power spectrum, $P(k)$, as a function of cosmological parameters can be prohibitively slow in cosmological analyses, hence emulating this calculation is desirable. Previous analytic approximations are insufficiently accurate for modern applications, so black-box, uninterpretable emulators are often used. We utilise an efficient genetic programming based symbolic regression framework to explore the space of potential mathematical expressions which can approximate the power spectrum and $\sigma_8$. We learn the ratio between an existing low-accuracy fitting function for $P(k)$ and that obtained by solving the Boltzmann equations and thus still incorporate the physics which motivated this earlier approximation. We obtain an analytic approximation to the linear power spectrum with a root mean squared fractional error of 0.2% between $k = 9\times10^{-3} - 9 \, h{\rm \, Mpc^{-1}}$ and across a wide range of cosmological parameters, and we provide physical interpretations for various terms in the expression. We also provide a simple analytic approximation for $\sigma_8$ with a similar accuracy, with a root mean squared fractional error of just 0.4% when evaluated across the same range of cosmologies. This function is easily invertible to obtain $A_{\rm s}$ as a function of $\sigma_8$ and the other cosmological parameters, if preferred. It is possible to obtain symbolic approximations to a seemingly complex function at a precision required for current and future cosmological analyses without resorting to deep-learning techniques, thus avoiding their black-box nature and large number of parameters. Our emulator will be usable long after the codes on which numerical approximations are built become outdated.

Symbolic Regression with Fast Function Extraction and Nonlinear Least Squares Optimization

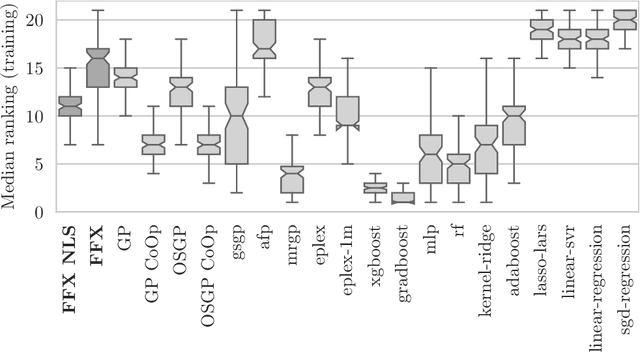
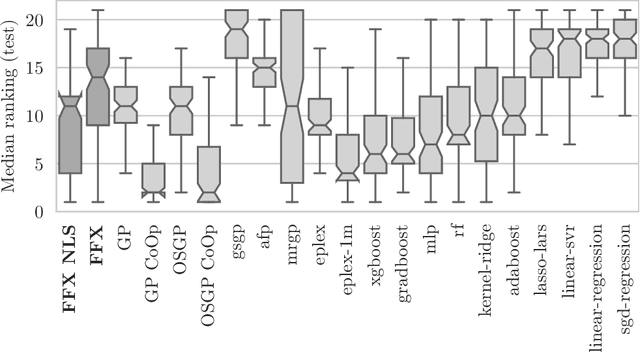
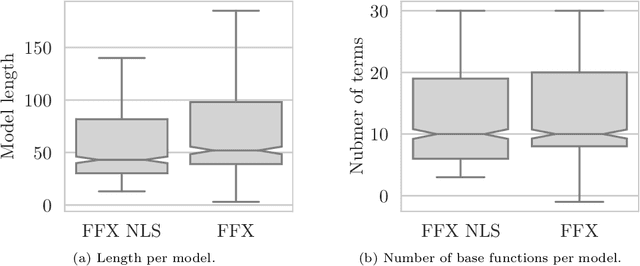
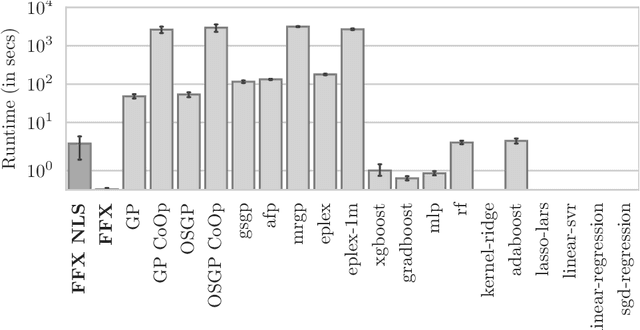
Fast Function Extraction (FFX) is a deterministic algorithm for solving symbolic regression problems. We improve the accuracy of FFX by adding parameters to the arguments of nonlinear functions. Instead of only optimizing linear parameters, we optimize these additional nonlinear parameters with separable nonlinear least squared optimization using a variable projection algorithm. Both FFX and our new algorithm is applied on the PennML benchmark suite. We show that the proposed extensions of FFX leads to higher accuracy while providing models of similar length and with only a small increase in runtime on the given data. Our results are compared to a large set of regression methods that were already published for the given benchmark suite.

Cluster Analysis of a Symbolic Regression Search Space

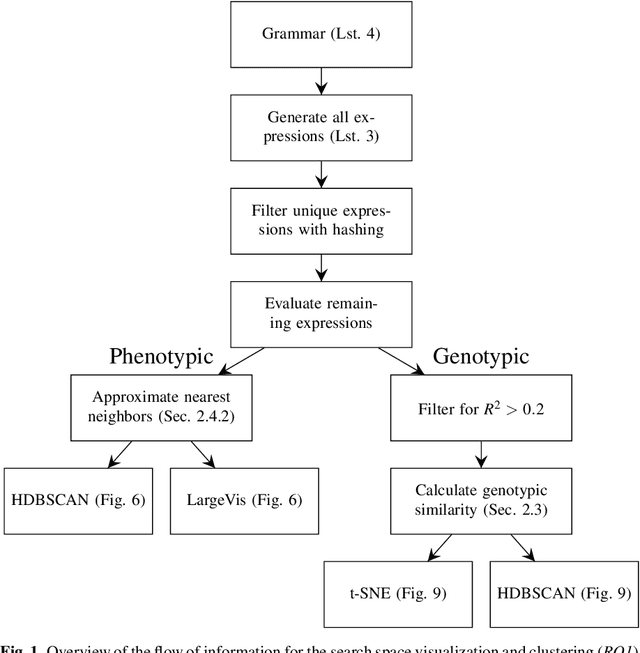
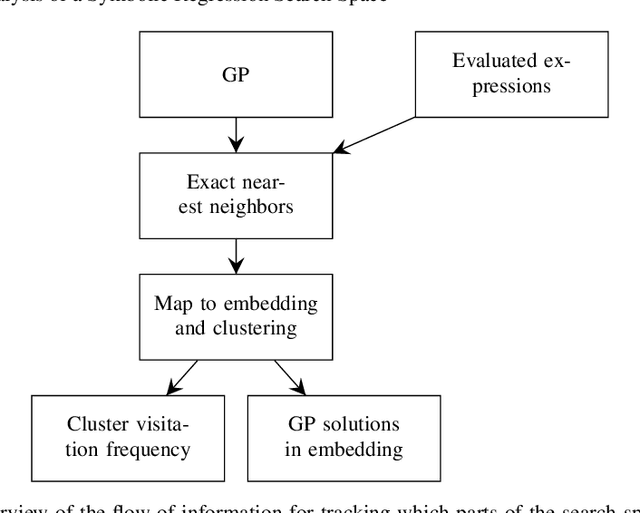
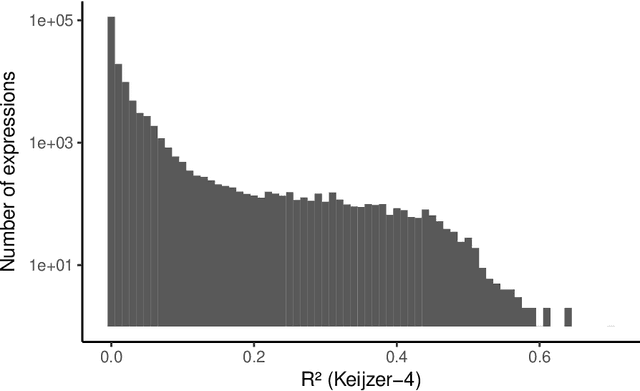
In this chapter we take a closer look at the distribution of symbolic regression models generated by genetic programming in the search space. The motivation for this work is to improve the search for well-fitting symbolic regression models by using information about the similarity of models that can be precomputed independently from the target function. For our analysis, we use a restricted grammar for uni-variate symbolic regression models and generate all possible models up to a fixed length limit. We identify unique models and cluster them based on phenotypic as well as genotypic similarity. We find that phenotypic similarity leads to well-defined clusters while genotypic similarity does not produce a clear clustering. By mapping solution candidates visited by GP to the enumerated search space we find that GP initially explores the whole search space and later converges to the subspace of highest quality expressions in a run for a simple benchmark problem.

Symbolic Regression by Exhaustive Search: Reducing the Search Space Using Syntactical Constraints and Efficient Semantic Structure Deduplication

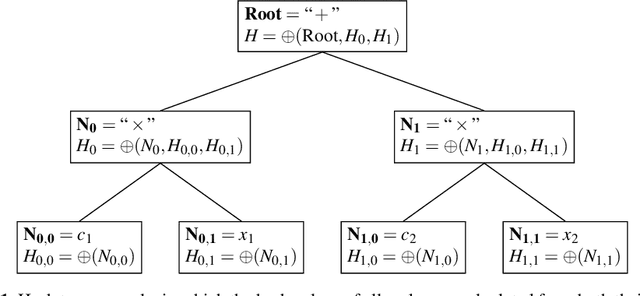
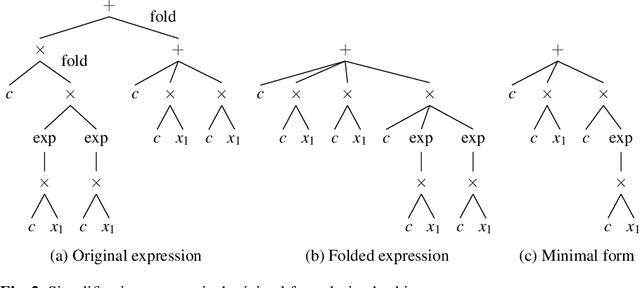
Symbolic regression is a powerful system identification technique in industrial scenarios where no prior knowledge on model structure is available. Such scenarios often require specific model properties such as interpretability, robustness, trustworthiness and plausibility, that are not easily achievable using standard approaches like genetic programming for symbolic regression. In this chapter we introduce a deterministic symbolic regression algorithm specifically designed to address these issues. The algorithm uses a context-free grammar to produce models that are parameterized by a non-linear least squares local optimization procedure. A finite enumeration of all possible models is guaranteed by structural restrictions as well as a caching mechanism for detecting semantically equivalent solutions. Enumeration order is established via heuristics designed to improve search efficiency. Empirical tests on a comprehensive benchmark suite show that our approach is competitive with genetic programming in many noiseless problems while maintaining desirable properties such as simple, reliable models and reproducibility.

Data Aggregation for Reducing Training Data in Symbolic Regression

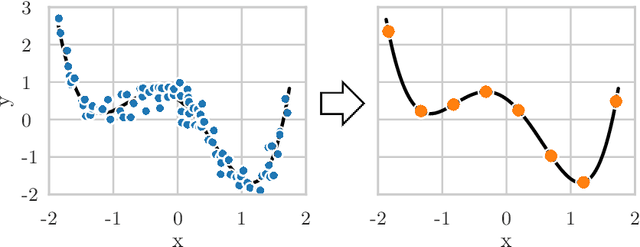
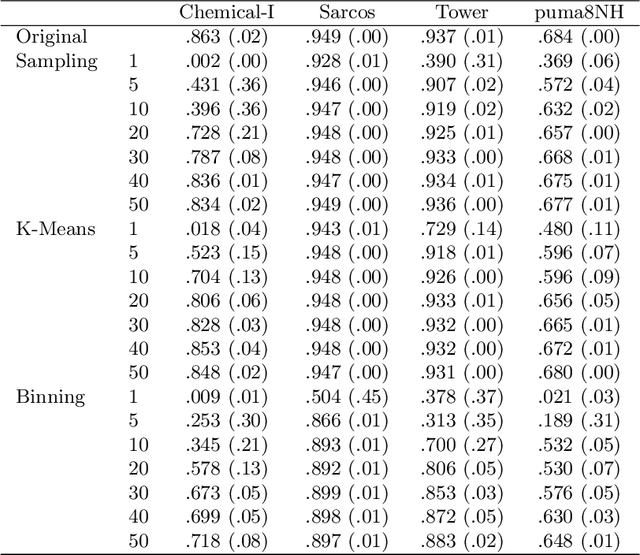
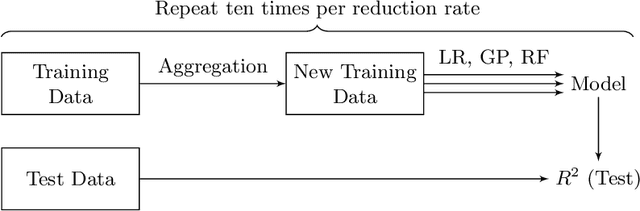
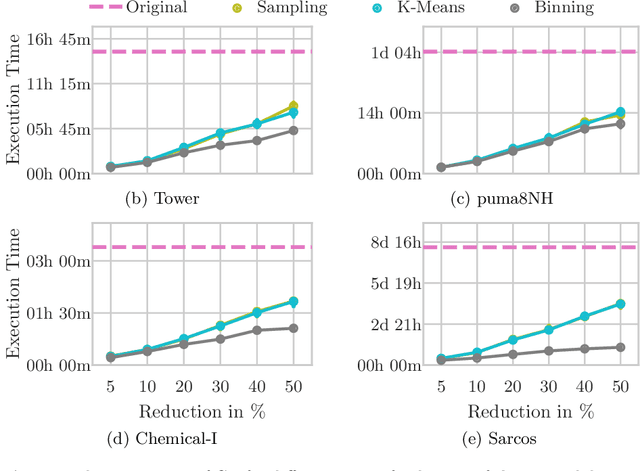
The growing volume of data makes the use of computationally intense machine learning techniques such as symbolic regression with genetic programming more and more impractical. This work discusses methods to reduce the training data and thereby also the runtime of genetic programming. The data is aggregated in a preprocessing step before running the actual machine learning algorithm. K-means clustering and data binning is used for data aggregation and compared with random sampling as the simplest data reduction method. We analyze the achieved speed-up in training and the effects on the trained models test accuracy for every method on four real-world data sets. The performance of genetic programming is compared with random forests and linear regression. It is shown, that k-means and random sampling lead to very small loss in test accuracy when the data is reduced down to only 30% of the original data, while the speed-up is proportional to the size of the data set. Binning on the contrary, leads to models with very high test error.

Hash-Based Tree Similarity and Simplification in Genetic Programming for Symbolic Regression

We introduce in this paper a runtime-efficient tree hashing algorithm for the identification of isomorphic subtrees, with two important applications in genetic programming for symbolic regression: fast, online calculation of population diversity and algebraic simplification of symbolic expression trees. Based on this hashing approach, we propose a simple diversity-preservation mechanism with promising results on a collection of symbolic regression benchmark problems.

Identification of Dynamical Systems using Symbolic Regression

We describe a method for the identification of models for dynamical systems from observational data. The method is based on the concept of symbolic regression and uses genetic programming to evolve a system of ordinary differential equations (ODE). The novelty is that we add a step of gradient-based optimization of the ODE parameters. For this we calculate the sensitivities of the solution to the initial value problem (IVP) using automatic differentiation. The proposed approach is tested on a set of 19 problem instances taken from the literature which includes datasets from simulated systems as well as datasets captured from mechanical systems. We find that gradient-based optimization of parameters improves predictive accuracy of the models. The best results are obtained when we first fit the individual equations to the numeric differences and then subsequently fine-tune the identified parameter values by fitting the IVP solution to the observed variable values.