Towards Vertical Privacy-Preserving Symbolic Regression via Secure Multiparty Computation

Symbolic Regression is a powerful data-driven technique that searches for mathematical expressions that explain the relationship between input variables and a target of interest. Due to its efficiency and flexibility, Genetic Programming can be seen as the standard search technique for Symbolic Regression. However, the conventional Genetic Programming algorithm requires storing all data in a central location, which is not always feasible due to growing concerns about data privacy and security. While privacy-preserving research has advanced recently and might offer a solution to this problem, their application to Symbolic Regression remains largely unexplored. Furthermore, the existing work only focuses on the horizontally partitioned setting, whereas the vertically partitioned setting, another popular scenario, has yet to be investigated. Herein, we propose an approach that employs a privacy-preserving technique called Secure Multiparty Computation to enable parties to jointly build Symbolic Regression models in the vertical scenario without revealing private data. Preliminary experimental results indicate that our proposed method delivers comparable performance to the centralized solution while safeguarding data privacy.

Probabilistic Distance-Based Outlier Detection

The scores of distance-based outlier detection methods are difficult to interpret, making it challenging to determine a cut-off threshold between normal and outlier data points without additional context. We describe a generic transformation of distance-based outlier scores into interpretable, probabilistic estimates. The transformation is ranking-stable and increases the contrast between normal and outlier data points. Determining distance relationships between data points is necessary to identify the nearest-neighbor relationships in the data, yet, most of the computed distances are typically discarded. We show that the distances to other data points can be used to model distance probability distributions and, subsequently, use the distributions to turn distance-based outlier scores into outlier probabilities. Our experiments show that the probabilistic transformation does not impact detection performance over numerous tabular and image benchmark datasets but results in interpretable outlier scores with increased contrast between normal and outlier samples. Our work generalizes to a wide range of distance-based outlier detection methods, and because existing distance computations are used, it adds no significant computational overhead.

Vectorial Genetic Programming -- Optimizing Segments for Feature Extraction

Vectorial Genetic Programming (Vec-GP) extends GP by allowing vectors as input features along regular, scalar features, using them by applying arithmetic operations component-wise or aggregating vectors into scalars by some aggregation function. Vec-GP also allows aggregating vectors only over a limited segment of the vector instead of the whole vector, which offers great potential but also introduces new parameters that GP has to optimize. This paper formalizes an optimization problem to analyze different strategies for optimizing a window for aggregation functions. Different strategies are presented, included random and guided sampling, where the latter leverages information from an approximated gradient. Those strategies can be applied as a simple optimization algorithm, which itself ca be applied inside a specialized mutation operator within GP. The presented results indicate, that the different random sampling strategies do not impact the overall algorithm performance significantly, and that the guided strategies suffer from becoming stuck in local optima. However, results also indicate, that there is still potential in discovering more efficient algorithms that could outperform the presented strategies.

OutlierDetection.jl: A modular outlier detection ecosystem for the Julia programming language

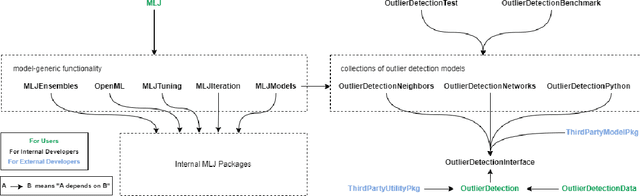
OutlierDetection.jl is an open-source ecosystem for outlier detection in Julia. It provides a range of high-performance outlier detection algorithms implemented directly in Julia. In contrast to previous packages, our ecosystem enables the development highly-scalable outlier detection algorithms using a high-level programming language. Additionally, it provides a standardized, yet flexible, interface for future outlier detection algorithms and allows for model composition unseen in previous packages. Best practices such as unit testing, continuous integration, and code coverage reporting are enforced across the ecosystem. The most recent version of OutlierDetection.jl is available at https://github.com/OutlierDetectionJL/OutlierDetection.jl.

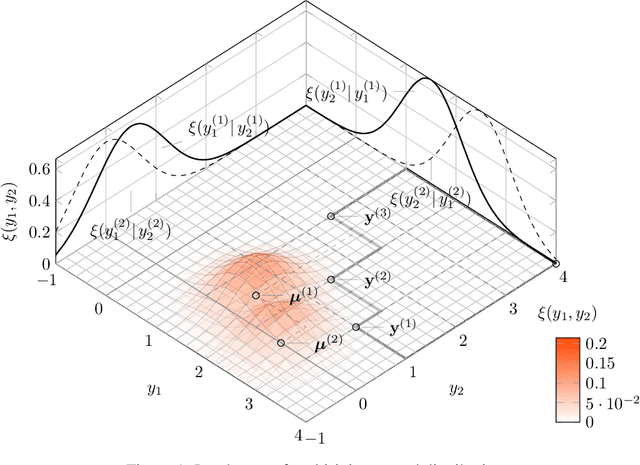
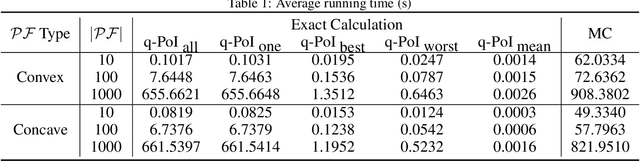
A Parallel Technique for Multi-objective Bayesian Global Optimization: Using a Batch Selection of Probability of Improvement

Bayesian global optimization (BGO) is an efficient surrogate-assisted technique for problems involving expensive evaluations. A parallel technique can be used to parallelly evaluate the true-expensive objective functions in one iteration to boost the execution time. An effective and straightforward approach is to design an acquisition function that can evaluate the performance of a bath of multiple solutions, instead of a single point/solution, in one iteration. This paper proposes five alternatives of \emph{Probability of Improvement} (PoI) with multiple points in a batch (q-PoI) for multi-objective Bayesian global optimization (MOBGO), taking the covariance among multiple points into account. Both exact computational formulas and the Monte Carlo approximation algorithms for all proposed q-PoIs are provided. Based on the distribution of the multiple points relevant to the Pareto-front, the position-dependent behavior of the five q-PoIs is investigated. Moreover, the five q-PoIs are compared with the other nine state-of-the-art and recently proposed batch MOBGO algorithms on twenty bio-objective benchmarks. The empirical experiments on different variety of benchmarks are conducted to demonstrate the effectiveness of two greedy q-PoIs ($\kpoi_{\mbox{best}}$ and $\kpoi_{\mbox{all}}$) on low-dimensional problems and the effectiveness of two explorative q-PoIs ($\kpoi_{\mbox{one}}$ and $\kpoi_{\mbox{worst}}$) on high-dimensional problems with difficult-to-approximate Pareto front boundaries.

Symbolic Regression in Materials Science: Discovering Interatomic Potentials from Data

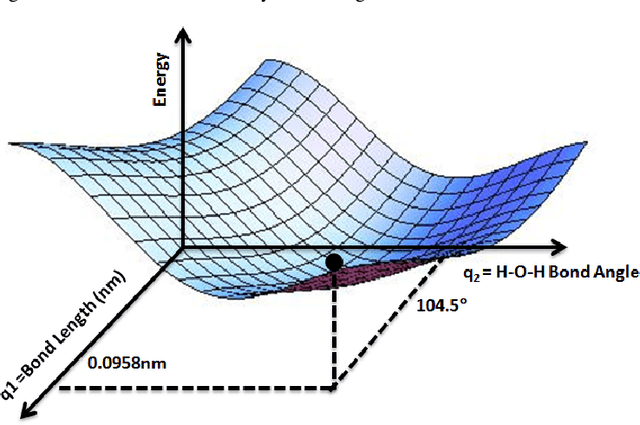
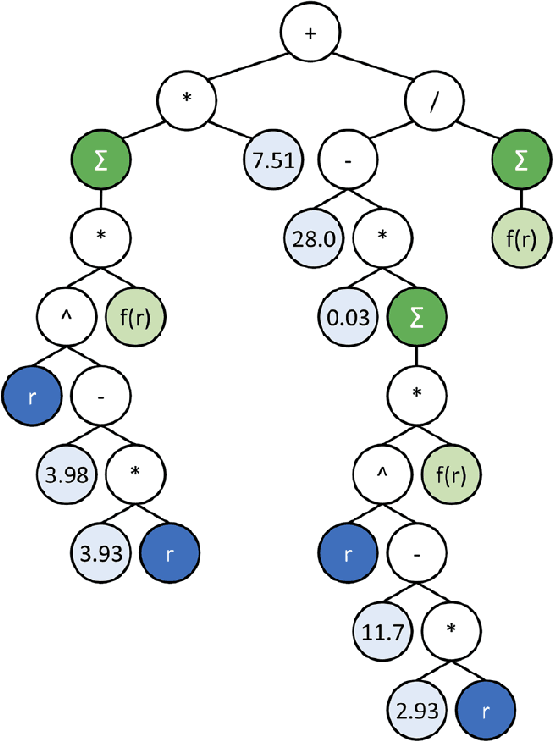
Particle-based modeling of materials at atomic scale plays an important role in the development of new materials and understanding of their properties. The accuracy of particle simulations is determined by interatomic potentials, which allow to calculate the potential energy of an atomic system as a function of atomic coordinates and potentially other properties. First-principles-based ab initio potentials can reach arbitrary levels of accuracy, however their aplicability is limited by their high computational cost. Machine learning (ML) has recently emerged as an effective way to offset the high computational costs of ab initio atomic potentials by replacing expensive models with highly efficient surrogates trained on electronic structure data. Among a plethora of current methods, symbolic regression (SR) is gaining traction as a powerful "white-box" approach for discovering functional forms of interatomic potentials. This contribution discusses the role of symbolic regression in Materials Science (MS) and offers a comprehensive overview of current methodological challenges and state-of-the-art results. A genetic programming-based approach for modeling atomic potentials from raw data (consisting of snapshots of atomic positions and associated potential energy) is presented and empirically validated on ab initio electronic structure data.

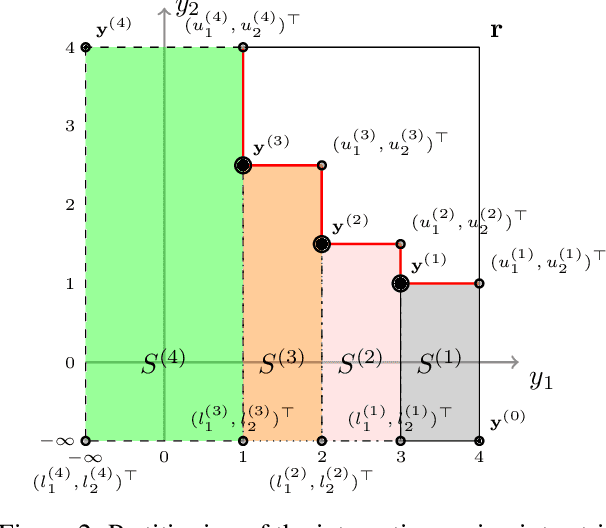
Probability Distribution of Hypervolume Improvement in Bi-objective Bayesian Optimization

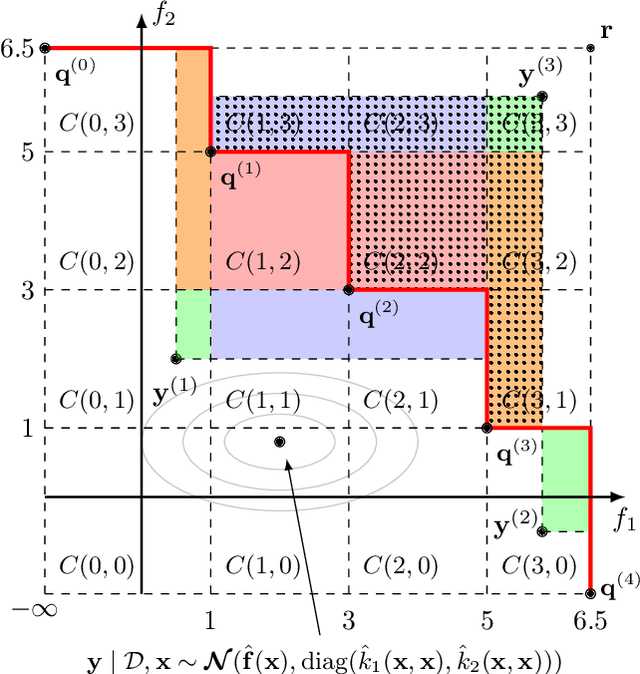
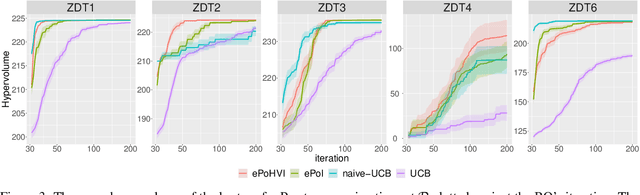
This work provides the exact expression of the probability distribution of the hypervolume improvement (HVI) for bi-objective generalization of Bayesian optimization. Here, instead of a single-objective improvement, we consider the improvement of the hypervolume indicator concerning the current best approximation of the Pareto front. Gaussian process regression models are trained independently on both objective functions, resulting in a bi-variate separated Gaussian distribution serving as a predictive model for the vector-valued objective function. Some commonly HVI-based acquisition functions (probability of improvement and upper confidence bound) are also leveraged with the help of the exact distribution of HVI. In addition, we show the superior numerical accuracy and efficiency of the exact distribution compared to the commonly used approximation by Monte-Carlo sampling. Finally, we benchmark distribution-leveraged acquisition functions on the widely applied ZDT problem set, demonstrating a significant advantage of using the exact distribution of HVI in multi-objective Bayesian optimization.

Cluster Analysis of a Symbolic Regression Search Space

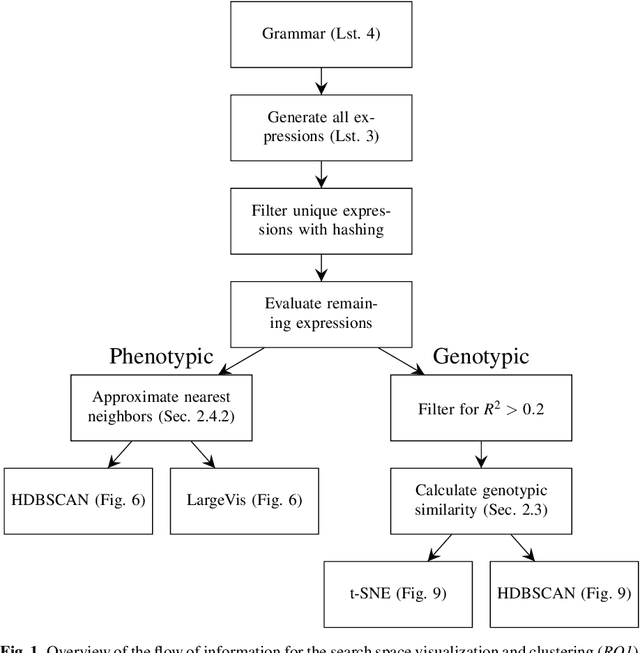
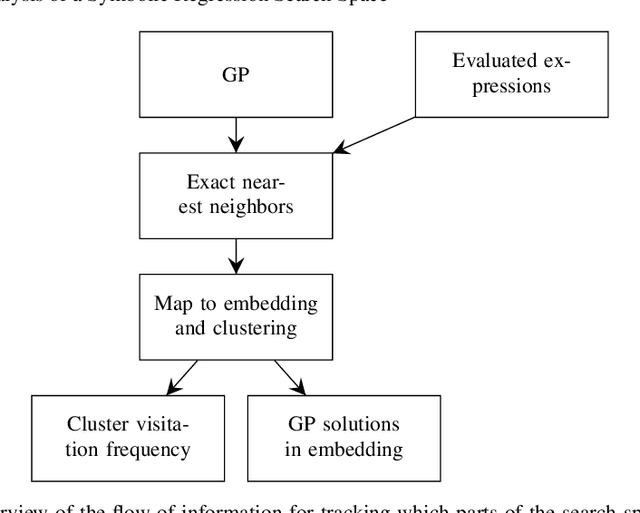
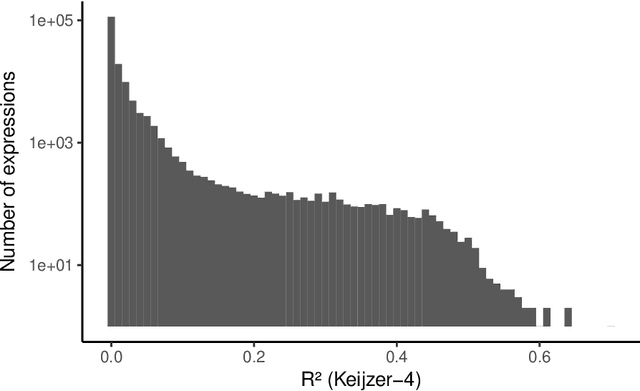
In this chapter we take a closer look at the distribution of symbolic regression models generated by genetic programming in the search space. The motivation for this work is to improve the search for well-fitting symbolic regression models by using information about the similarity of models that can be precomputed independently from the target function. For our analysis, we use a restricted grammar for uni-variate symbolic regression models and generate all possible models up to a fixed length limit. We identify unique models and cluster them based on phenotypic as well as genotypic similarity. We find that phenotypic similarity leads to well-defined clusters while genotypic similarity does not produce a clear clustering. By mapping solution candidates visited by GP to the enumerated search space we find that GP initially explores the whole search space and later converges to the subspace of highest quality expressions in a run for a simple benchmark problem.

Symbolic Regression by Exhaustive Search: Reducing the Search Space Using Syntactical Constraints and Efficient Semantic Structure Deduplication

Symbolic regression is a powerful system identification technique in industrial scenarios where no prior knowledge on model structure is available. Such scenarios often require specific model properties such as interpretability, robustness, trustworthiness and plausibility, that are not easily achievable using standard approaches like genetic programming for symbolic regression. In this chapter we introduce a deterministic symbolic regression algorithm specifically designed to address these issues. The algorithm uses a context-free grammar to produce models that are parameterized by a non-linear least squares local optimization procedure. A finite enumeration of all possible models is guaranteed by structural restrictions as well as a caching mechanism for detecting semantically equivalent solutions. Enumeration order is established via heuristics designed to improve search efficiency. Empirical tests on a comprehensive benchmark suite show that our approach is competitive with genetic programming in many noiseless problems while maintaining desirable properties such as simple, reliable models and reproducibility.

Complexity Measures for Multi-objective Symbolic Regression

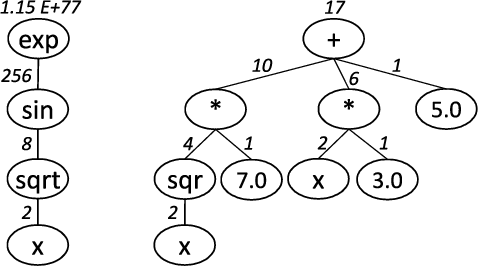
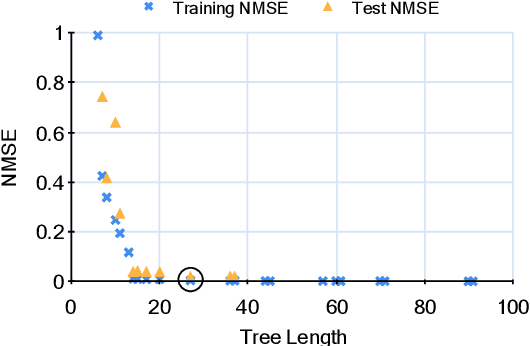
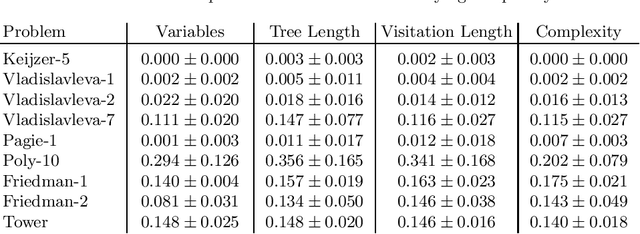
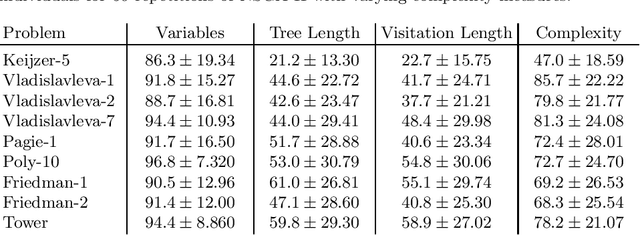
Multi-objective symbolic regression has the advantage that while the accuracy of the learned models is maximized, the complexity is automatically adapted and need not be specified a-priori. The result of the optimization is not a single solution anymore, but a whole Pareto-front describing the trade-off between accuracy and complexity. In this contribution we study which complexity measures are most appropriately used in symbolic regression when performing multi- objective optimization with NSGA-II. Furthermore, we present a novel complexity measure that includes semantic information based on the function symbols occurring in the models and test its effects on several benchmark datasets. Results comparing multiple complexity measures are presented in terms of the achieved accuracy and model length to illustrate how the search direction of the algorithm is affected.