Nuclear Morphometry using a Deep Learning-based Algorithm has Prognostic Relevance for Canine Cutaneous Mast Cell Tumors

Variation in nuclear size and shape is an important criterion of malignancy for many tumor types; however, categorical estimates by pathologists have poor reproducibility. Measurements of nuclear characteristics (morphometry) can improve reproducibility, but manual methods are time consuming. In this study, we evaluated fully automated morphometry using a deep learning-based algorithm in 96 canine cutaneous mast cell tumors with information on patient survival. Algorithmic morphometry was compared with karyomegaly estimates by 11 pathologists, manual nuclear morphometry of 12 cells by 9 pathologists, and the mitotic count as a benchmark. The prognostic value of automated morphometry was high with an area under the ROC curve regarding the tumor-specific survival of 0.943 (95% CI: 0.889 - 0.996) for the standard deviation (SD) of nuclear area, which was higher than manual morphometry of all pathologists combined (0.868, 95% CI: 0.737 - 0.991) and the mitotic count (0.885, 95% CI: 0.765 - 1.00). At the proposed thresholds, the hazard ratio for algorithmic morphometry (SD of nuclear area $\geq 9.0 \mu m^2$) was 18.3 (95% CI: 5.0 - 67.1), for manual morphometry (SD of nuclear area $\geq 10.9 \mu m^2$) 9.0 (95% CI: 6.0 - 13.4), for karyomegaly estimates 7.6 (95% CI: 5.7 - 10.1), and for the mitotic count 30.5 (95% CI: 7.8 - 118.0). Inter-rater reproducibility for karyomegaly estimates was fair ($\kappa$ = 0.226) with highly variable sensitivity/specificity values for the individual pathologists. Reproducibility for manual morphometry (SD of nuclear area) was good (ICC = 0.654). This study supports the use of algorithmic morphometry as a prognostic test to overcome the limitations of estimates and manual measurements.

Cluster Analysis of a Symbolic Regression Search Space

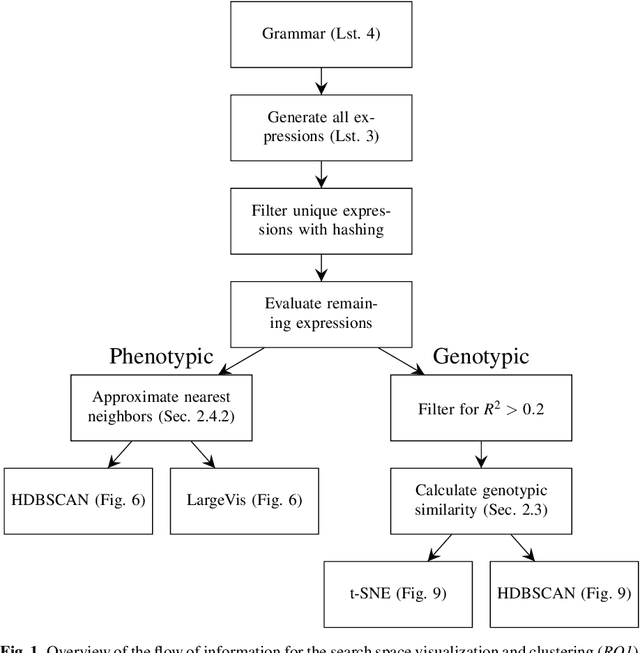
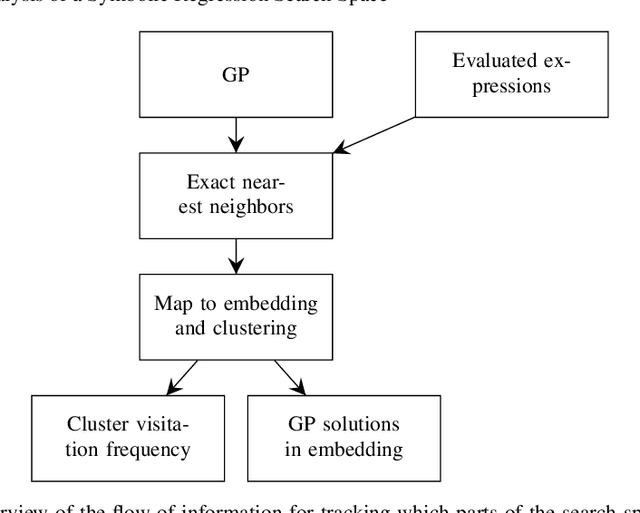
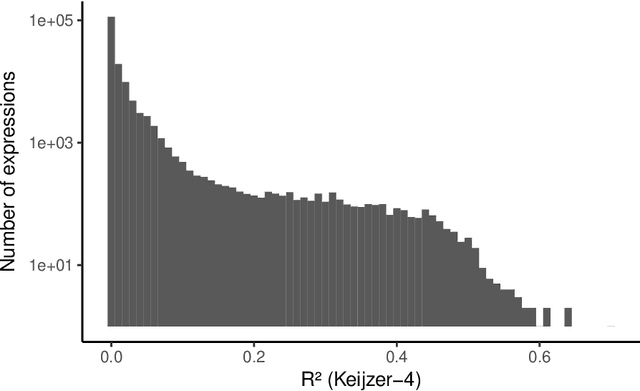
In this chapter we take a closer look at the distribution of symbolic regression models generated by genetic programming in the search space. The motivation for this work is to improve the search for well-fitting symbolic regression models by using information about the similarity of models that can be precomputed independently from the target function. For our analysis, we use a restricted grammar for uni-variate symbolic regression models and generate all possible models up to a fixed length limit. We identify unique models and cluster them based on phenotypic as well as genotypic similarity. We find that phenotypic similarity leads to well-defined clusters while genotypic similarity does not produce a clear clustering. By mapping solution candidates visited by GP to the enumerated search space we find that GP initially explores the whole search space and later converges to the subspace of highest quality expressions in a run for a simple benchmark problem.

Symbolic Regression by Exhaustive Search: Reducing the Search Space Using Syntactical Constraints and Efficient Semantic Structure Deduplication

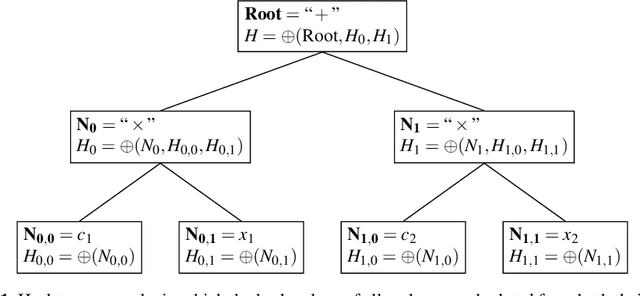
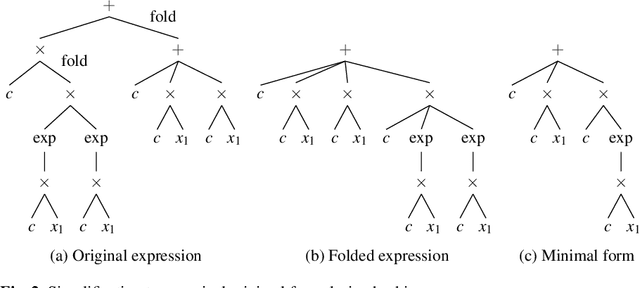
Symbolic regression is a powerful system identification technique in industrial scenarios where no prior knowledge on model structure is available. Such scenarios often require specific model properties such as interpretability, robustness, trustworthiness and plausibility, that are not easily achievable using standard approaches like genetic programming for symbolic regression. In this chapter we introduce a deterministic symbolic regression algorithm specifically designed to address these issues. The algorithm uses a context-free grammar to produce models that are parameterized by a non-linear least squares local optimization procedure. A finite enumeration of all possible models is guaranteed by structural restrictions as well as a caching mechanism for detecting semantically equivalent solutions. Enumeration order is established via heuristics designed to improve search efficiency. Empirical tests on a comprehensive benchmark suite show that our approach is competitive with genetic programming in many noiseless problems while maintaining desirable properties such as simple, reliable models and reproducibility.