Multi-View Symbolic Regression

Symbolic regression (SR) searches for analytical expressions representing the relationship between a set of explanatory and response variables. Current SR methods assume a single dataset extracted from a single experiment. Nevertheless, frequently, the researcher is confronted with multiple sets of results obtained from experiments conducted with different setups. Traditional SR methods may fail to find the underlying expression since the parameters of each experiment can be different. In this work we present Multi-View Symbolic Regression (MvSR), which takes into account multiple datasets simultaneously, mimicking experimental environments, and outputs a general parametric solution. This approach fits the evaluated expression to each independent dataset and returns a parametric family of functions f(x; \theta) simultaneously capable of accurately fitting all datasets. We demonstrate the effectiveness of MvSR using data generated from known expressions, as well as real-world data from astronomy, chemistry and economy, for which an a priori analytical expression is not available. Results show that MvSR obtains the correct expression more frequently and is robust to hyperparameters change. In real-world data, it is able to grasp the group behaviour, recovering known expressions from the literature as well as promising alternatives, thus enabling the use SR to a large range of experimental scenarios.

A precise symbolic emulator of the linear matter power spectrum

Computing the matter power spectrum, $P(k)$, as a function of cosmological parameters can be prohibitively slow in cosmological analyses, hence emulating this calculation is desirable. Previous analytic approximations are insufficiently accurate for modern applications, so black-box, uninterpretable emulators are often used. We utilise an efficient genetic programming based symbolic regression framework to explore the space of potential mathematical expressions which can approximate the power spectrum and $\sigma_8$. We learn the ratio between an existing low-accuracy fitting function for $P(k)$ and that obtained by solving the Boltzmann equations and thus still incorporate the physics which motivated this earlier approximation. We obtain an analytic approximation to the linear power spectrum with a root mean squared fractional error of 0.2% between $k = 9\times10^{-3} - 9 \, h{\rm \, Mpc^{-1}}$ and across a wide range of cosmological parameters, and we provide physical interpretations for various terms in the expression. We also provide a simple analytic approximation for $\sigma_8$ with a similar accuracy, with a root mean squared fractional error of just 0.4% when evaluated across the same range of cosmologies. This function is easily invertible to obtain $A_{\rm s}$ as a function of $\sigma_8$ and the other cosmological parameters, if preferred. It is possible to obtain symbolic approximations to a seemingly complex function at a precision required for current and future cosmological analyses without resorting to deep-learning techniques, thus avoiding their black-box nature and large number of parameters. Our emulator will be usable long after the codes on which numerical approximations are built become outdated.

Symbolic Regression in Materials Science: Discovering Interatomic Potentials from Data

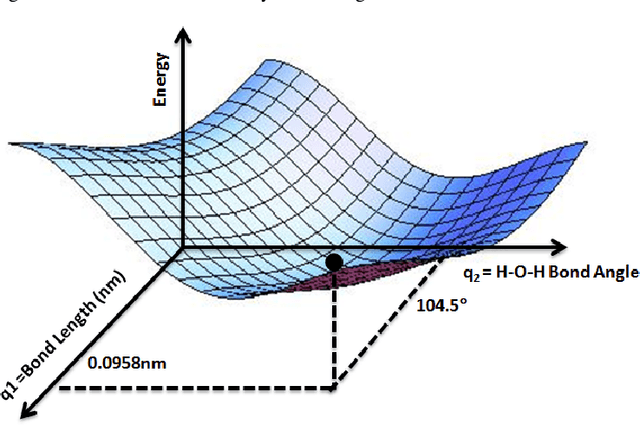
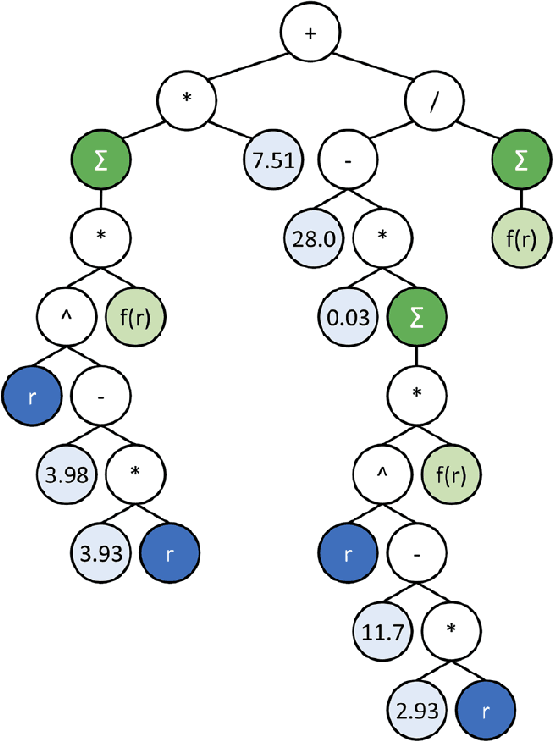
Particle-based modeling of materials at atomic scale plays an important role in the development of new materials and understanding of their properties. The accuracy of particle simulations is determined by interatomic potentials, which allow to calculate the potential energy of an atomic system as a function of atomic coordinates and potentially other properties. First-principles-based ab initio potentials can reach arbitrary levels of accuracy, however their aplicability is limited by their high computational cost. Machine learning (ML) has recently emerged as an effective way to offset the high computational costs of ab initio atomic potentials by replacing expensive models with highly efficient surrogates trained on electronic structure data. Among a plethora of current methods, symbolic regression (SR) is gaining traction as a powerful "white-box" approach for discovering functional forms of interatomic potentials. This contribution discusses the role of symbolic regression in Materials Science (MS) and offers a comprehensive overview of current methodological challenges and state-of-the-art results. A genetic programming-based approach for modeling atomic potentials from raw data (consisting of snapshots of atomic positions and associated potential energy) is presented and empirically validated on ab initio electronic structure data.

Rank-based Non-dominated Sorting

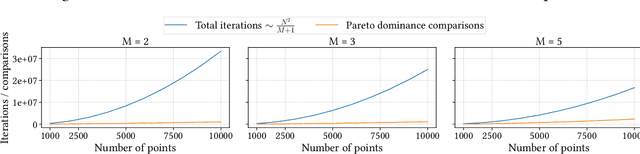
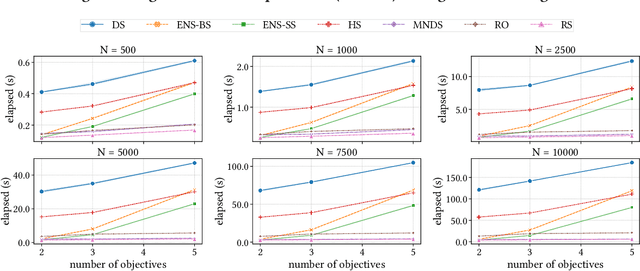
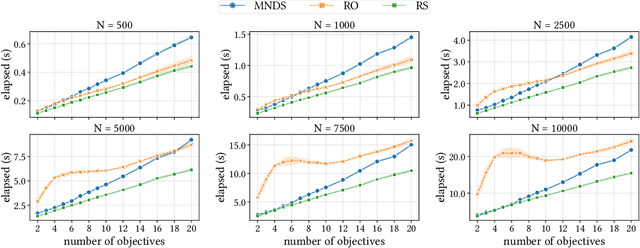
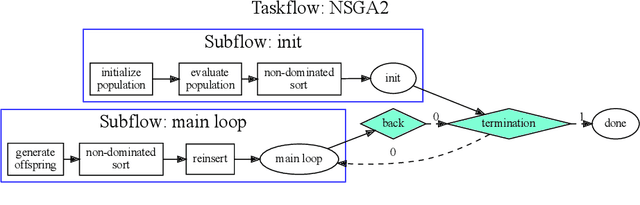
Non-dominated sorting is a computational bottleneck in Pareto-based multi-objective evolutionary algorithms (MOEAs) due to the runtime-intensive comparison operations involved in establishing dominance relationships between solution candidates. In this paper we introduce Rank Sort, a non-dominated sorting approach exploiting sorting stability and ordinal information to avoid expensive dominance comparisons in the rank assignment phase. Two algorithmic variants are proposed: the first one, RankOrdinal (RO), uses ordinal rank comparisons in order to determine dominance and requires O(N) space; the second one, RankIntersect (RS), uses set intersections and bit-level parallelism and requires O(N^2) space. We demonstrate the efficiency of the proposed methods in comparison with other state of the art algorithms in empirical simulations using the NSGA2 algorithm as well as synthetic benchmarks. The RankIntersect algorithm is able to significantly outperform the current state of the art offering up to 30% speed-up for many objectives. C++ implementations are provided for all algorithms.

Cluster Analysis of a Symbolic Regression Search Space

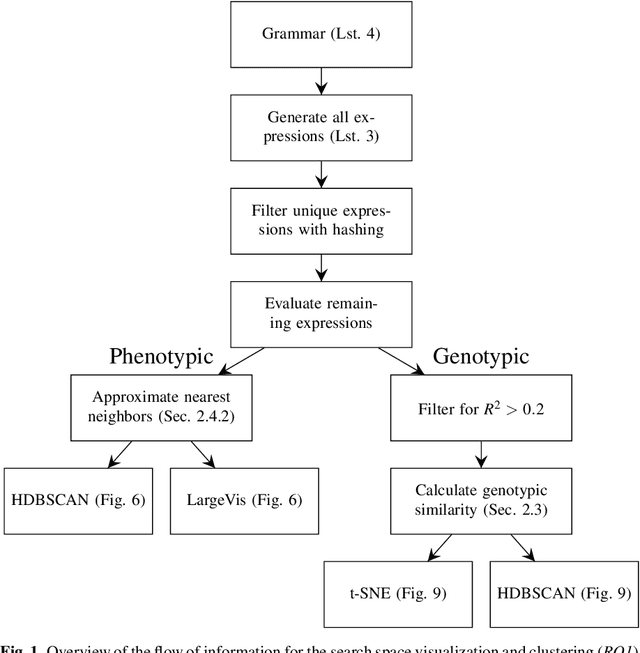
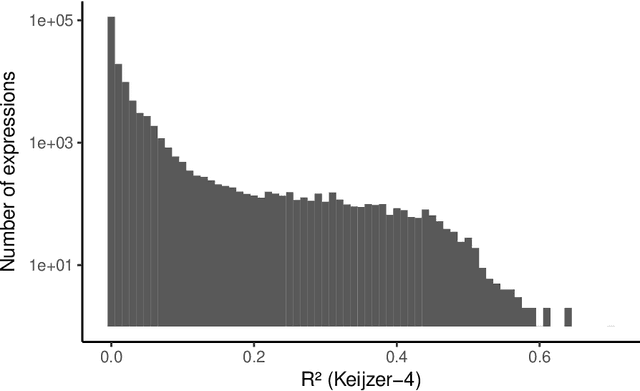
In this chapter we take a closer look at the distribution of symbolic regression models generated by genetic programming in the search space. The motivation for this work is to improve the search for well-fitting symbolic regression models by using information about the similarity of models that can be precomputed independently from the target function. For our analysis, we use a restricted grammar for uni-variate symbolic regression models and generate all possible models up to a fixed length limit. We identify unique models and cluster them based on phenotypic as well as genotypic similarity. We find that phenotypic similarity leads to well-defined clusters while genotypic similarity does not produce a clear clustering. By mapping solution candidates visited by GP to the enumerated search space we find that GP initially explores the whole search space and later converges to the subspace of highest quality expressions in a run for a simple benchmark problem.

Symbolic Regression by Exhaustive Search: Reducing the Search Space Using Syntactical Constraints and Efficient Semantic Structure Deduplication

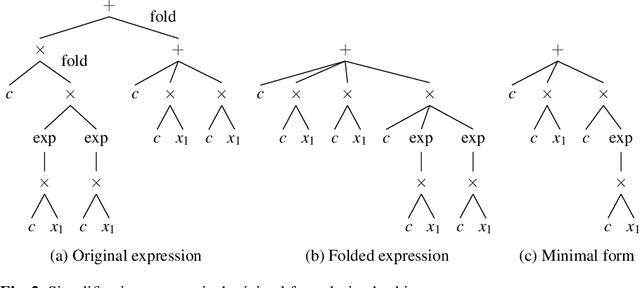
Symbolic regression is a powerful system identification technique in industrial scenarios where no prior knowledge on model structure is available. Such scenarios often require specific model properties such as interpretability, robustness, trustworthiness and plausibility, that are not easily achievable using standard approaches like genetic programming for symbolic regression. In this chapter we introduce a deterministic symbolic regression algorithm specifically designed to address these issues. The algorithm uses a context-free grammar to produce models that are parameterized by a non-linear least squares local optimization procedure. A finite enumeration of all possible models is guaranteed by structural restrictions as well as a caching mechanism for detecting semantically equivalent solutions. Enumeration order is established via heuristics designed to improve search efficiency. Empirical tests on a comprehensive benchmark suite show that our approach is competitive with genetic programming in many noiseless problems while maintaining desirable properties such as simple, reliable models and reproducibility.

On the Effectiveness of Genetic Operations in Symbolic Regression

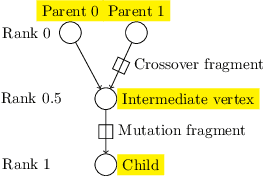
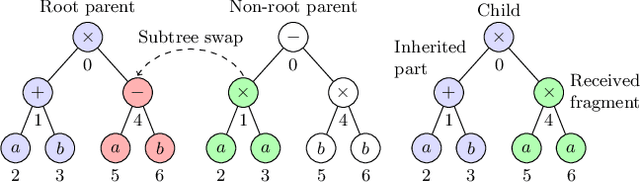
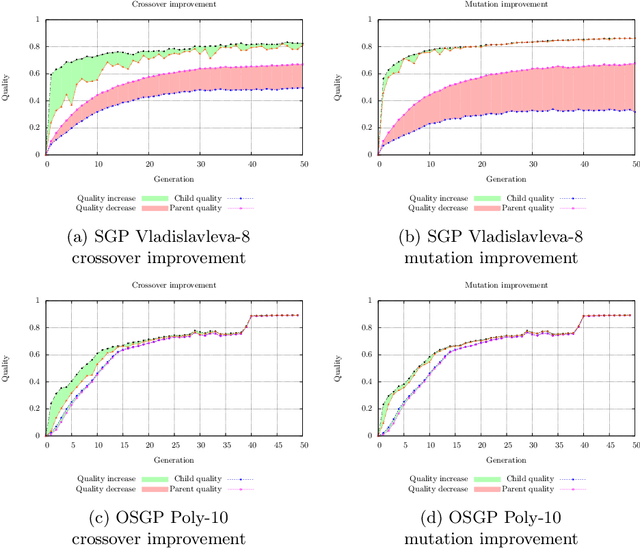
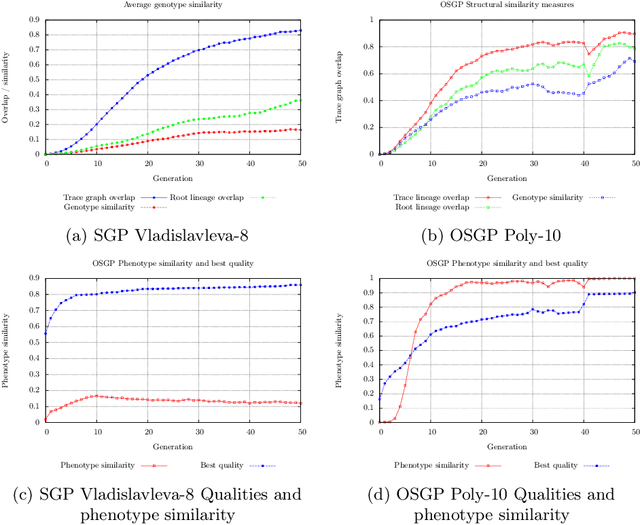
This paper describes a methodology for analyzing the evolutionary dynamics of genetic programming (GP) using genealogical information, diversity measures and information about the fitness variation from parent to offspring. We introduce a new subtree tracing approach for identifying the origins of genes in the structure of individuals, and we show that only a small fraction of ancestor individuals are responsible for the evolvement of the best solutions in the population.

Contemporary Symbolic Regression Methods and their Relative Performance

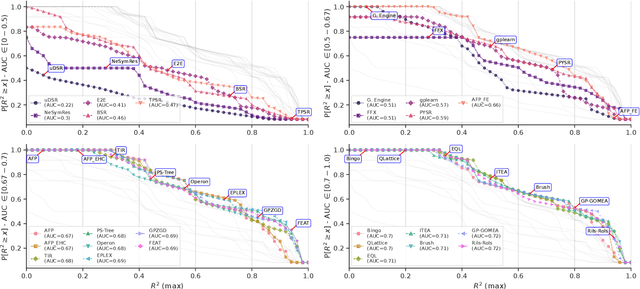
Many promising approaches to symbolic regression have been presented in recent years, yet progress in the field continues to suffer from a lack of uniform, robust, and transparent benchmarking standards. In this paper, we address this shortcoming by introducing an open-source, reproducible benchmarking platform for symbolic regression. We assess 14 symbolic regression methods and 7 machine learning methods on a set of 252 diverse regression problems. Our assessment includes both real-world datasets with no known model form as well as ground-truth benchmark problems, including physics equations and systems of ordinary differential equations. For the real-world datasets, we benchmark the ability of each method to learn models with low error and low complexity relative to state-of-the-art machine learning methods. For the synthetic problems, we assess each method's ability to find exact solutions in the presence of varying levels of noise. Under these controlled experiments, we conclude that the best performing methods for real-world regression combine genetic algorithms with parameter estimation and/or semantic search drivers. When tasked with recovering exact equations in the presence of noise, we find that deep learning and genetic algorithm-based approaches perform similarly. We provide a detailed guide to reproducing this experiment and contributing new methods, and encourage other researchers to collaborate with us on a common and living symbolic regression benchmark.

Hash-Based Tree Similarity and Simplification in Genetic Programming for Symbolic Regression

We introduce in this paper a runtime-efficient tree hashing algorithm for the identification of isomorphic subtrees, with two important applications in genetic programming for symbolic regression: fast, online calculation of population diversity and algebraic simplification of symbolic expression trees. Based on this hashing approach, we propose a simple diversity-preservation mechanism with promising results on a collection of symbolic regression benchmark problems.