Introduction to Symbolic Regression in the Physical Sciences

Symbolic regression (SR) has emerged as a powerful method for uncovering interpretable mathematical relationships from data, offering a novel route to both scientific discovery and efficient empirical modelling. This article introduces the Special Issue on Symbolic Regression for the Physical Sciences, motivated by the Royal Society discussion meeting held in April 2025. The contributions collected here span applications from automated equation discovery and emergent-phenomena modelling to the construction of compact emulators for computationally expensive simulations. The introductory review outlines the conceptual foundations of SR, contrasts it with conventional regression approaches, and surveys its main use cases in the physical sciences, including the derivation of effective theories, empirical functional forms and surrogate models. We summarise methodological considerations such as search-space design, operator selection, complexity control, feature selection, and integration with modern AI approaches. We also highlight ongoing challenges, including scalability, robustness to noise, overfitting and computational complexity. Finally we emphasise emerging directions, particularly the incorporation of symmetry constraints, asymptotic behaviour and other theoretical information. Taken together, the papers in this Special Issue illustrate the accelerating progress of SR and its growing relevance across the physical sciences.

syren-baryon: Analytic emulators for the impact of baryons on the matter power spectrum

Baryonic physics has a considerable impact on the distribution of matter in our Universe on scales probed by current and future cosmological surveys, acting as a key systematic in such analyses. We seek simple symbolic parametrisations for the impact of baryonic physics on the matter power spectrum for a range of physically motivated models, as a function of wavenumber, redshift, cosmology, and parameters controlling the baryonic feedback. We use symbolic regression to construct analytic approximations for the ratio of the matter power spectrum in the presence of baryons to that without such effects. We obtain separate functions of each of four distinct sub-grid prescriptions of baryonic physics from the CAMELS suite of hydrodynamical simulations (Astrid, IllustrisTNG, SIMBA and Swift-EAGLE) as well as for a baryonification algorithm. We also provide functions which describe the uncertainty on these predictions, due to both the stochastic nature of baryonic physics and the errors on our fits. The error on our approximations to the hydrodynamical simulations is comparable to the sample variance estimated through varying initial conditions, and our baryonification expression has a root mean squared error of better than one percent, although this increases on small scales. These errors are comparable to those of previous numerical emulators for these models. Our expressions are enforced to have the physically correct behaviour on large scales and at high redshift. Due to their analytic form, we are able to directly interpret the impact of varying cosmology and feedback parameters, and we can identify parameters which have little to no effect. Each function is based on a different implementation of baryonic physics, and can therefore be used to discriminate between these models when applied to real data. We provide publicly available code for all symbolic approximations found.

syren-new: Precise formulae for the linear and nonlinear matter power spectra with massive neutrinos and dynamical dark energy

Current and future large scale structure surveys aim to constrain the neutrino mass and the equation of state of dark energy. We aim to construct accurate and interpretable symbolic approximations to the linear and nonlinear matter power spectra as a function of cosmological parameters in extended $\Lambda$CDM models which contain massive neutrinos and non-constant equations of state for dark energy. This constitutes an extension of the syren-halofit emulators to incorporate these two effects, which we call syren-new (SYmbolic-Regression-ENhanced power spectrum emulator with NEutrinos and $W_0-w_a$). We also obtain a simple approximation to the derived parameter $\sigma_8$ as a function of the cosmological parameters for these models. Our results for the linear power spectrum are designed to emulate CLASS, whereas for the nonlinear case we aim to match the results of EuclidEmulator2. We compare our results to existing emulators and $N$-body simulations. Our analytic emulators for $\sigma_8$, the linear and nonlinear power spectra achieve root mean squared errors of 0.1%, 0.3% and 1.3%, respectively, across a wide range of cosmological parameters, redshifts and wavenumbers. We verify that emulator-related discrepancies are subdominant compared to observational errors and other modelling uncertainties when computing shear power spectra for LSST-like surveys. Our expressions have similar accuracy to existing (numerical) emulators, but are at least an order of magnitude faster, both on a CPU and GPU. Our work greatly improves the accuracy, speed and range of applicability of current symbolic approximations to the linear and nonlinear matter power spectra. We provide publicly available code for all symbolic approximations found.

CHARM: Creating Halos with Auto-Regressive Multi-stage networks

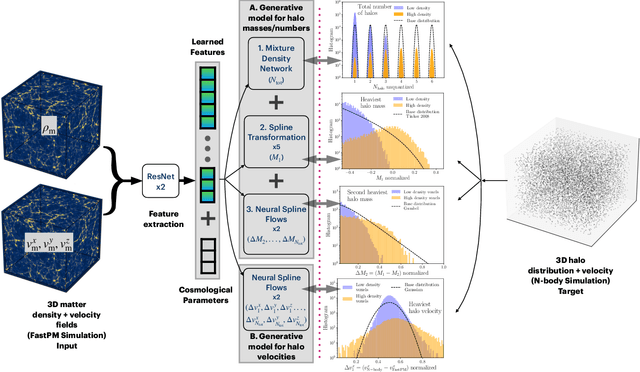
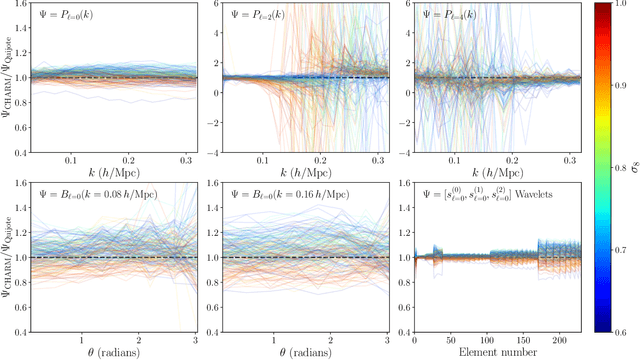
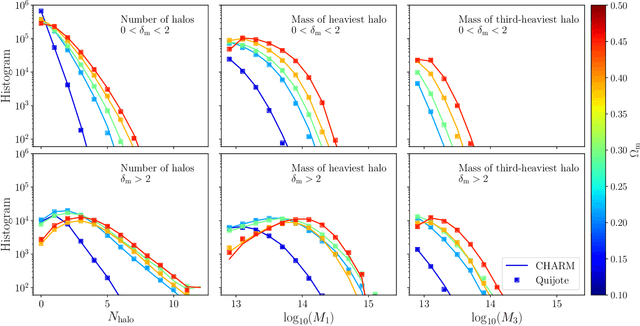
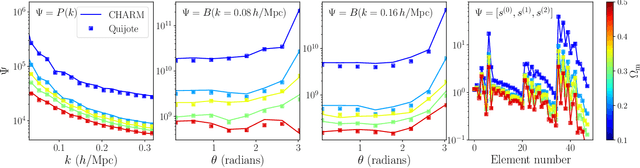
To maximize the amount of information extracted from cosmological datasets, simulations that accurately represent these observations are necessary. However, traditional simulations that evolve particles under gravity by estimating particle-particle interactions (N-body simulations) are computationally expensive and prohibitive to scale to the large volumes and resolutions necessary for the upcoming datasets. Moreover, modeling the distribution of galaxies typically involves identifying virialized dark matter halos, which is also a time- and memory-consuming process for large N-body simulations, further exacerbating the computational cost. In this study, we introduce CHARM, a novel method for creating mock halo catalogs by matching the spatial, mass, and velocity statistics of halos directly from the large-scale distribution of the dark matter density field. We develop multi-stage neural spline flow-based networks to learn this mapping at redshift z=0.5 directly with computationally cheaper low-resolution particle mesh simulations instead of relying on the high-resolution N-body simulations. We show that the mock halo catalogs and painted galaxy catalogs have the same statistical properties as obtained from $N$-body simulations in both real space and redshift space. Finally, we use these mock catalogs for cosmological inference using redshift-space galaxy power spectrum, bispectrum, and wavelet-based statistics using simulation-based inference, performing the first inference with accelerated forward model simulations and finding unbiased cosmological constraints with well-calibrated posteriors. The code was developed as part of the Simons Collaboration on Learning the Universe and is publicly available at \url{https://github.com/shivampcosmo/CHARM}.

COmoving Computer Acceleration (COCA): $N$-body simulations in an emulated frame of reference

$N$-body simulations are computationally expensive, so machine-learning (ML)-based emulation techniques have emerged as a way to increase their speed. Although fast, surrogate models have limited trustworthiness due to potentially substantial emulation errors that current approaches cannot correct for. To alleviate this problem, we introduce COmoving Computer Acceleration (COCA), a hybrid framework interfacing ML with an $N$-body simulator. The correct physical equations of motion are solved in an emulated frame of reference, so that any emulation error is corrected by design. This approach corresponds to solving for the perturbation of particle trajectories around the machine-learnt solution, which is computationally cheaper than obtaining the full solution, yet is guaranteed to converge to the truth as one increases the number of force evaluations. Although applicable to any ML algorithm and $N$-body simulator, this approach is assessed in the particular case of particle-mesh cosmological simulations in a frame of reference predicted by a convolutional neural network, where the time dependence is encoded as an additional input parameter to the network. COCA efficiently reduces emulation errors in particle trajectories, requiring far fewer force evaluations than running the corresponding simulation without ML. We obtain accurate final density and velocity fields for a reduced computational budget. We demonstrate that this method shows robustness when applied to examples outside the range of the training data. When compared to the direct emulation of the Lagrangian displacement field using the same training resources, COCA's ability to correct emulation errors results in more accurate predictions. COCA makes $N$-body simulations cheaper by skipping unnecessary force evaluations, while still solving the correct equations of motion and correcting for emulation errors made by ML.

The Inefficiency of Genetic Programming for Symbolic Regression -- Extended Version

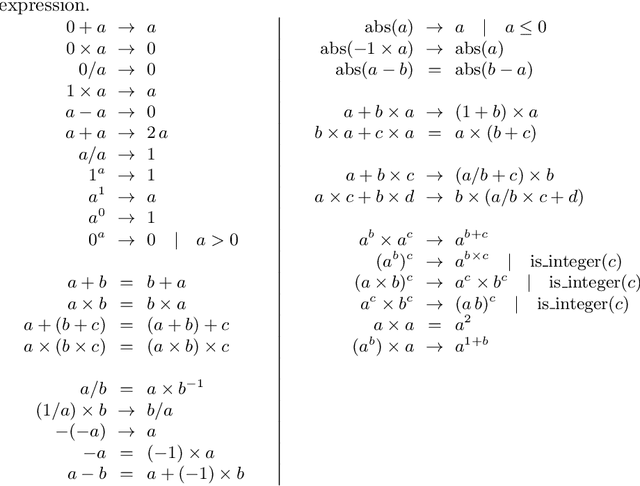
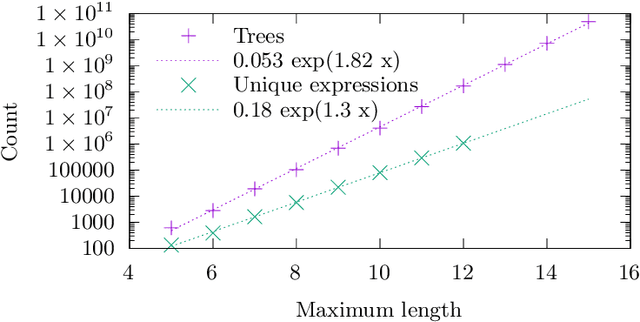
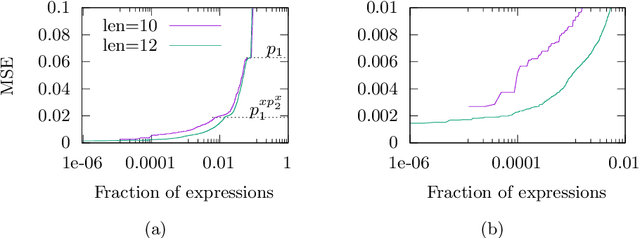
We analyse the search behaviour of genetic programming for symbolic regression in practically relevant but limited settings, allowing exhaustive enumeration of all solutions. This enables us to quantify the success probability of finding the best possible expressions, and to compare the search efficiency of genetic programming to random search in the space of semantically unique expressions. This analysis is made possible by improved algorithms for equality saturation, which we use to improve the Exhaustive Symbolic Regression algorithm; this produces the set of semantically unique expression structures, orders of magnitude smaller than the full symbolic regression search space. We compare the efficiency of random search in the set of unique expressions and genetic programming. For our experiments we use two real-world datasets where symbolic regression has been used to produce well-fitting univariate expressions: the Nikuradse dataset of flow in rough pipes and the Radial Acceleration Relation of galaxy dynamics. The results show that genetic programming in such limited settings explores only a small fraction of all unique expressions, and evaluates expressions repeatedly that are congruent to already visited expressions.

syren-halofit: A fast, interpretable, high-precision formula for the $Λ$CDM nonlinear matter power spectrum

Rapid and accurate evaluation of the nonlinear matter power spectrum, $P(k)$, as a function of cosmological parameters and redshift is of fundamental importance in cosmology. Analytic approximations provide an interpretable solution, yet current approximations are neither fast nor accurate relative to black-box numerical emulators. We use symbolic regression to obtain simple analytic approximations to the nonlinear scale, $k_\sigma$, the effective spectral index, $n_{\rm eff}$, and the curvature, $C$, which are required for the halofit model. We then re-optimise the coefficients of halofit to fit a wide range of cosmologies and redshifts. We then again exploit symbolic regression to explore the space of analytic expressions to fit the residuals between $P(k)$ and the optimised predictions of halofit. All methods are validated against $N$-body simulations. Our symbolic expressions for $k_\sigma$, $n_{\rm eff}$ and $C$ have root mean squared fractional errors of 0.8%, 0.2% and 0.3%, respectively, for redshifts below 3 and a wide range of cosmologies. The re-optimised halofit parameters reduce the root mean squared fractional error from 3% to below 2% for wavenumbers $k=9\times10^{-3}-9 \, h{\rm Mpc^{-1}}$. We introduce syren-halofit (symbolic-regression-enhanced halofit), an extension to halofit containing a short symbolic correction which improves this error to 1%. Our method is 2350 and 3170 times faster than current halofit and hmcode implementations, respectively, and 2680 and 64 times faster than EuclidEmulator2 (which requires running class) and the BACCO emulator. We obtain comparable accuracy to EuclidEmulator2 and the BACCO emulator when tested on $N$-body simulations. Our work greatly increases the speed and accuracy of symbolic approximations to $P(k)$, making them significantly faster than their numerical counterparts without loss of accuracy.

LtU-ILI: An All-in-One Framework for Implicit Inference in Astrophysics and Cosmology

This paper presents the Learning the Universe Implicit Likelihood Inference (LtU-ILI) pipeline, a codebase for rapid, user-friendly, and cutting-edge machine learning (ML) inference in astrophysics and cosmology. The pipeline includes software for implementing various neural architectures, training schema, priors, and density estimators in a manner easily adaptable to any research workflow. It includes comprehensive validation metrics to assess posterior estimate coverage, enhancing the reliability of inferred results. Additionally, the pipeline is easily parallelizable, designed for efficient exploration of modeling hyperparameters. To demonstrate its capabilities, we present real applications across a range of astrophysics and cosmology problems, such as: estimating galaxy cluster masses from X-ray photometry; inferring cosmology from matter power spectra and halo point clouds; characterising progenitors in gravitational wave signals; capturing physical dust parameters from galaxy colors and luminosities; and establishing properties of semi-analytic models of galaxy formation. We also include exhaustive benchmarking and comparisons of all implemented methods as well as discussions about the challenges and pitfalls of ML inference in astronomical sciences. All code and examples are made publicly available at https://github.com/maho3/ltu-ili.

A precise symbolic emulator of the linear matter power spectrum

Computing the matter power spectrum, $P(k)$, as a function of cosmological parameters can be prohibitively slow in cosmological analyses, hence emulating this calculation is desirable. Previous analytic approximations are insufficiently accurate for modern applications, so black-box, uninterpretable emulators are often used. We utilise an efficient genetic programming based symbolic regression framework to explore the space of potential mathematical expressions which can approximate the power spectrum and $\sigma_8$. We learn the ratio between an existing low-accuracy fitting function for $P(k)$ and that obtained by solving the Boltzmann equations and thus still incorporate the physics which motivated this earlier approximation. We obtain an analytic approximation to the linear power spectrum with a root mean squared fractional error of 0.2% between $k = 9\times10^{-3} - 9 \, h{\rm \, Mpc^{-1}}$ and across a wide range of cosmological parameters, and we provide physical interpretations for various terms in the expression. We also provide a simple analytic approximation for $\sigma_8$ with a similar accuracy, with a root mean squared fractional error of just 0.4% when evaluated across the same range of cosmologies. This function is easily invertible to obtain $A_{\rm s}$ as a function of $\sigma_8$ and the other cosmological parameters, if preferred. It is possible to obtain symbolic approximations to a seemingly complex function at a precision required for current and future cosmological analyses without resorting to deep-learning techniques, thus avoiding their black-box nature and large number of parameters. Our emulator will be usable long after the codes on which numerical approximations are built become outdated.

The Simplest Inflationary Potentials

Inflation is a highly favoured theory for the early Universe. It is compatible with current observations of the cosmic microwave background and large scale structure and is a driver in the quest to detect primordial gravitational waves. It is also, given the current quality of the data, highly under-determined with a large number of candidate implementations. We use a new method in symbolic regression to generate all possible simple scalar field potentials for one of two possible basis sets of operators. Treating these as single-field, slow-roll inflationary models we then score them with an information-theoretic metric ("minimum description length") that quantifies their efficiency in compressing the information in the Planck data. We explore two possible priors on the parameter space of potentials, one related to the functions' structural complexity and one that uses a Katz back-off language model to prefer functions that may be theoretically motivated. This enables us to identify the inflaton potentials that optimally balance simplicity with accuracy at explaining the Planck data, which may subsequently find theoretical motivation. Our exploratory study opens the door to extraction of fundamental physics directly from data, and may be augmented with more refined theoretical priors in the quest for a complete understanding of the early Universe.