A Comparison of Recent Algorithms for Symbolic Regression to Genetic Programming

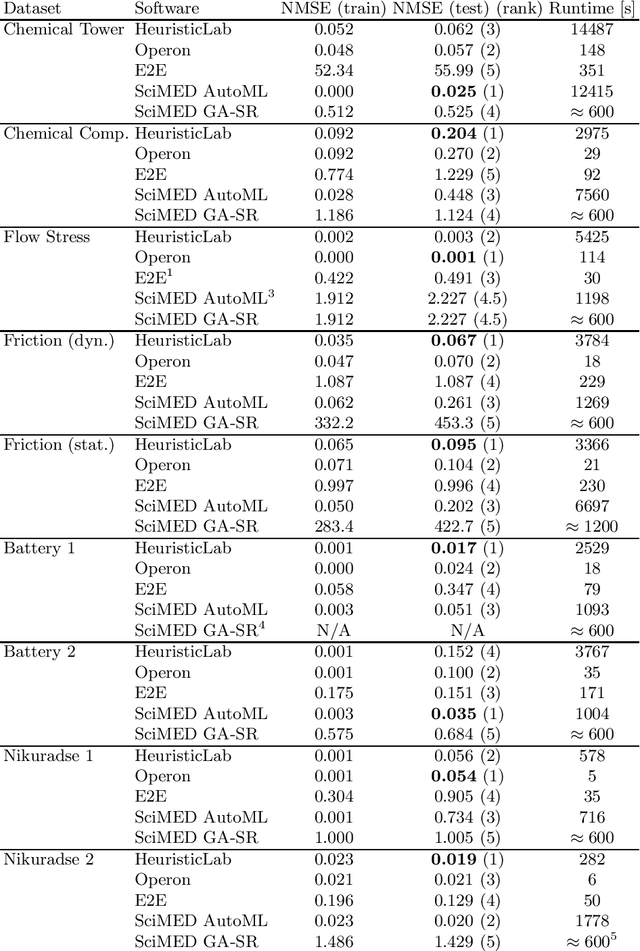
Symbolic regression is a machine learning method with the goal to produce interpretable results. Unlike other machine learning methods such as, e.g. random forests or neural networks, which are opaque, symbolic regression aims to model and map data in a way that can be understood by scientists. Recent advancements, have attempted to bridge the gap between these two fields; new methodologies attempt to fuse the mapping power of neural networks and deep learning techniques with the explanatory power of symbolic regression. In this paper, we examine these new emerging systems and test the performance of an end-to-end transformer model for symbolic regression versus the reigning traditional methods based on genetic programming that have spearheaded symbolic regression throughout the years. We compare these systems on novel datasets to avoid bias to older methods who were improved on well-known benchmark datasets. Our results show that traditional GP methods as implemented e.g., by Operon still remain superior to two recently published symbolic regression methods.

Vectorial Genetic Programming -- Optimizing Segments for Feature Extraction

Vectorial Genetic Programming (Vec-GP) extends GP by allowing vectors as input features along regular, scalar features, using them by applying arithmetic operations component-wise or aggregating vectors into scalars by some aggregation function. Vec-GP also allows aggregating vectors only over a limited segment of the vector instead of the whole vector, which offers great potential but also introduces new parameters that GP has to optimize. This paper formalizes an optimization problem to analyze different strategies for optimizing a window for aggregation functions. Different strategies are presented, included random and guided sampling, where the latter leverages information from an approximated gradient. Those strategies can be applied as a simple optimization algorithm, which itself ca be applied inside a specialized mutation operator within GP. The presented results indicate, that the different random sampling strategies do not impact the overall algorithm performance significantly, and that the guided strategies suffer from becoming stuck in local optima. However, results also indicate, that there is still potential in discovering more efficient algorithms that could outperform the presented strategies.

Identifying Differential Equations to predict Blood Glucose using Sparse Identification of Nonlinear Systems

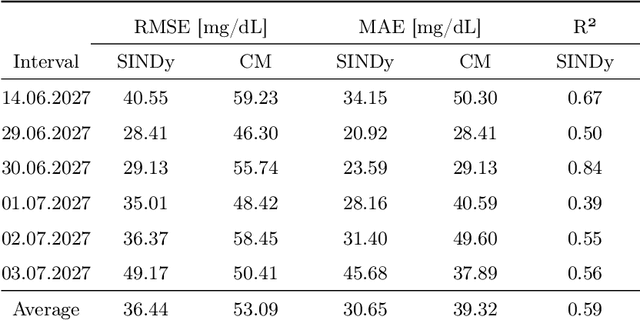
Describing dynamic medical systems using machine learning is a challenging topic with a wide range of applications. In this work, the possibility of modeling the blood glucose level of diabetic patients purely on the basis of measured data is described. A combination of the influencing variables insulin and calories are used to find an interpretable model. The absorption speed of external substances in the human body depends strongly on external influences, which is why time-shifts are added for the influencing variables. The focus is put on identifying the best timeshifts that provide robust models with good prediction accuracy that are independent of other unknown external influences. The modeling is based purely on the measured data using Sparse Identification of Nonlinear Dynamics. A differential equation is determined which, starting from an initial value, simulates blood glucose dynamics. By applying the best model to test data, we can show that it is possible to simulate the long-term blood glucose dynamics using differential equations and few, influencing variables.

Symbolic Regression in Materials Science: Discovering Interatomic Potentials from Data

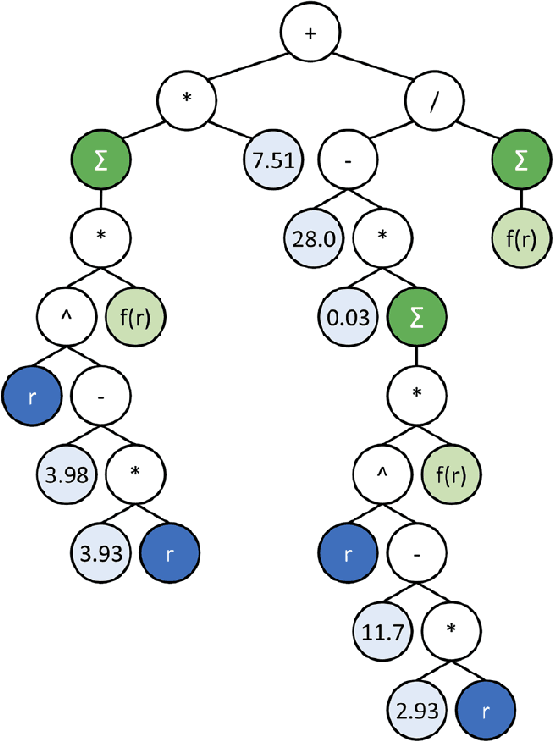
Particle-based modeling of materials at atomic scale plays an important role in the development of new materials and understanding of their properties. The accuracy of particle simulations is determined by interatomic potentials, which allow to calculate the potential energy of an atomic system as a function of atomic coordinates and potentially other properties. First-principles-based ab initio potentials can reach arbitrary levels of accuracy, however their aplicability is limited by their high computational cost. Machine learning (ML) has recently emerged as an effective way to offset the high computational costs of ab initio atomic potentials by replacing expensive models with highly efficient surrogates trained on electronic structure data. Among a plethora of current methods, symbolic regression (SR) is gaining traction as a powerful "white-box" approach for discovering functional forms of interatomic potentials. This contribution discusses the role of symbolic regression in Materials Science (MS) and offers a comprehensive overview of current methodological challenges and state-of-the-art results. A genetic programming-based approach for modeling atomic potentials from raw data (consisting of snapshots of atomic positions and associated potential energy) is presented and empirically validated on ab initio electronic structure data.

On the Success Rate of Crossover Operators for Genetic Programming with Offspring Selection

Genetic programming is a powerful heuristic search technique that is used for a number of real world applications to solve among others regression, classification, and time-series forecasting problems. A lot of progress towards a theoretic description of genetic programming in form of schema theorems has been made, but the internal dynamics and success factors of genetic programming are still not fully understood. In particular, the effects of different crossover operators in combination with offspring selection are largely unknown. This contribution sheds light on the ability of well-known GP crossover operators to create better offspring when applied to benchmark problems. We conclude that standard (sub-tree swapping) crossover is a good default choice in combination with offspring selection, and that GP with offspring selection and random selection of crossover operators can improve the performance of the algorithm in terms of best solution quality when no solution size constraints are applied.