Complexity Measures for Multi-objective Symbolic Regression

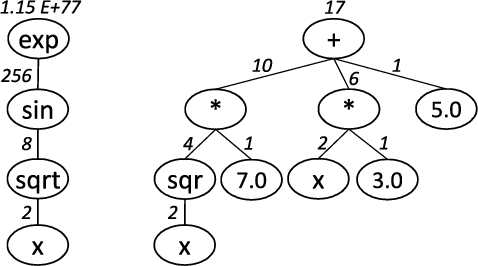
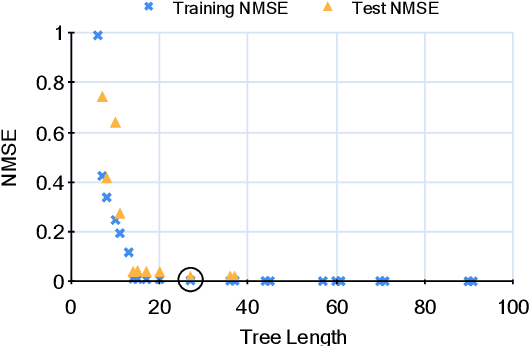
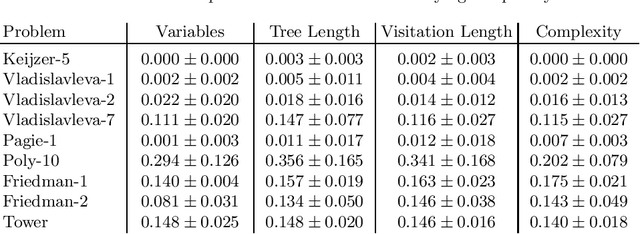
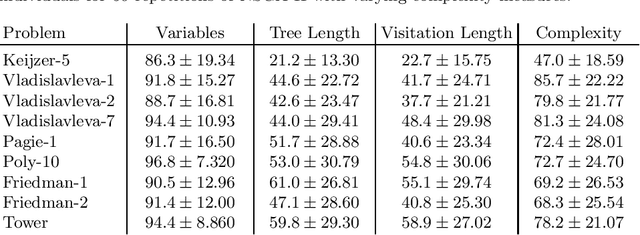
Multi-objective symbolic regression has the advantage that while the accuracy of the learned models is maximized, the complexity is automatically adapted and need not be specified a-priori. The result of the optimization is not a single solution anymore, but a whole Pareto-front describing the trade-off between accuracy and complexity. In this contribution we study which complexity measures are most appropriately used in symbolic regression when performing multi- objective optimization with NSGA-II. Furthermore, we present a novel complexity measure that includes semantic information based on the function symbols occurring in the models and test its effects on several benchmark datasets. Results comparing multiple complexity measures are presented in terms of the achieved accuracy and model length to illustrate how the search direction of the algorithm is affected.

On constraint programming for a new flexible project scheduling problem with resource constraints

Real-world project scheduling often requires flexibility in terms of the selection and the exact length of alternative production activities. Moreover, the simultaneous scheduling of multiple lots is mandatory in many production planning applications. To meet these requirements, a new flexible resource-constrained multi-project scheduling problem is introduced where both decisions (activity selection flexibility and time flexibility) are integrated. Besides the minimization of makespan, two alternative objectives inspired by a steel industry application case are presented: maximization of balanced length of selected activities (time balance) and maximization of balanced resource utilization (resource balance). New mixed integer and constraint programming (CP) models are proposed for the developed integrated flexible project scheduling problem. The real-world applicability of the suggested CP models is shown by solving large steel industry instances with the CP Optimizer of IBM ILOG CPLEX. Furthermore, benchmark instances on flexible resource-constrained project scheduling problems (RCPSP) are solved to optimality.

On the Success Rate of Crossover Operators for Genetic Programming with Offspring Selection

Genetic programming is a powerful heuristic search technique that is used for a number of real world applications to solve among others regression, classification, and time-series forecasting problems. A lot of progress towards a theoretic description of genetic programming in form of schema theorems has been made, but the internal dynamics and success factors of genetic programming are still not fully understood. In particular, the effects of different crossover operators in combination with offspring selection are largely unknown. This contribution sheds light on the ability of well-known GP crossover operators to create better offspring when applied to benchmark problems. We conclude that standard (sub-tree swapping) crossover is a good default choice in combination with offspring selection, and that GP with offspring selection and random selection of crossover operators can improve the performance of the algorithm in terms of best solution quality when no solution size constraints are applied.