Virtual Memory for 3D Gaussian Splatting

3D Gaussian Splatting represents a breakthrough in the field of novel view synthesis. It establishes Gaussians as core rendering primitives for highly accurate real-world environment reconstruction. Recent advances have drastically increased the size of scenes that can be created. In this work, we present a method for rendering large and complex 3D Gaussian Splatting scenes using virtual memory. By leveraging well-established virtual memory and virtual texturing techniques, our approach efficiently identifies visible Gaussians and dynamically streams them to the GPU just in time for real-time rendering. Selecting only the necessary Gaussians for both storage and rendering results in reduced memory usage and effectively accelerates rendering, especially for highly complex scenes. Furthermore, we demonstrate how level of detail can be integrated into our proposed method to further enhance rendering speed for large-scale scenes. With an optimized implementation, we highlight key practical considerations and thoroughly evaluate the proposed technique and its impact on desktop and mobile devices.

Vectorial Genetic Programming -- Optimizing Segments for Feature Extraction

Vectorial Genetic Programming (Vec-GP) extends GP by allowing vectors as input features along regular, scalar features, using them by applying arithmetic operations component-wise or aggregating vectors into scalars by some aggregation function. Vec-GP also allows aggregating vectors only over a limited segment of the vector instead of the whole vector, which offers great potential but also introduces new parameters that GP has to optimize. This paper formalizes an optimization problem to analyze different strategies for optimizing a window for aggregation functions. Different strategies are presented, included random and guided sampling, where the latter leverages information from an approximated gradient. Those strategies can be applied as a simple optimization algorithm, which itself ca be applied inside a specialized mutation operator within GP. The presented results indicate, that the different random sampling strategies do not impact the overall algorithm performance significantly, and that the guided strategies suffer from becoming stuck in local optima. However, results also indicate, that there is still potential in discovering more efficient algorithms that could outperform the presented strategies.

Understanding and Preparing Data of Industrial Processes for Machine Learning Applications

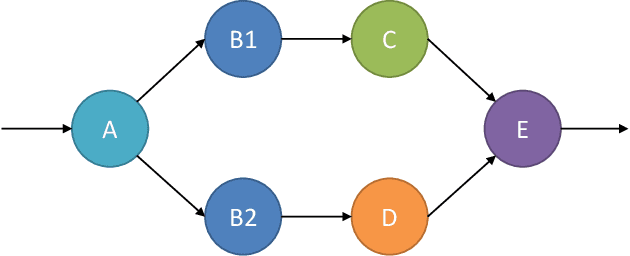
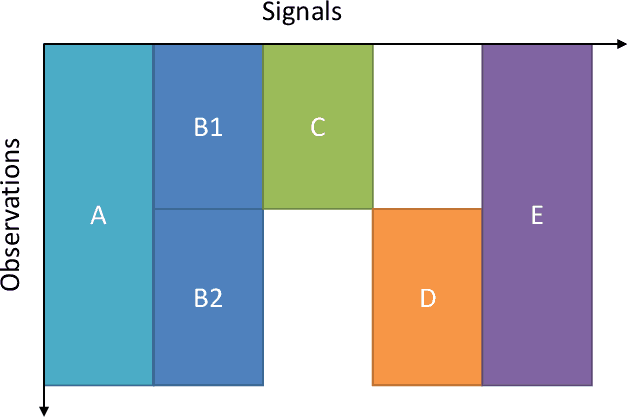
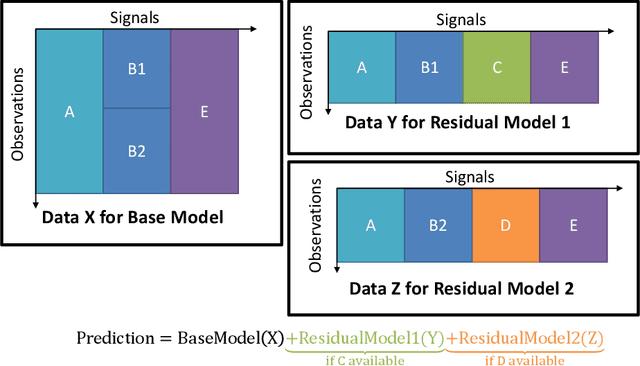
Industrial applications of machine learning face unique challenges due to the nature of raw industry data. Preprocessing and preparing raw industrial data for machine learning applications is a demanding task that often takes more time and work than the actual modeling process itself and poses additional challenges. This paper addresses one of those challenges, specifically, the challenge of missing values due to sensor unavailability at different production units of nonlinear production lines. In cases where only a small proportion of the data is missing, those missing values can often be imputed. In cases of large proportions of missing data, imputing is often not feasible, and removing observations containing missing values is often the only option. This paper presents a technique, that allows to utilize all of the available data without the need of removing large amounts of observations where data is only partially available. We do not only discuss the principal idea of the presented method, but also show different possible implementations that can be applied depending on the data at hand. Finally, we demonstrate the application of the presented method with data from a steel production plant.