Optimally Weighted Ensembles of Regression Models: Exact Weight Optimization and Applications

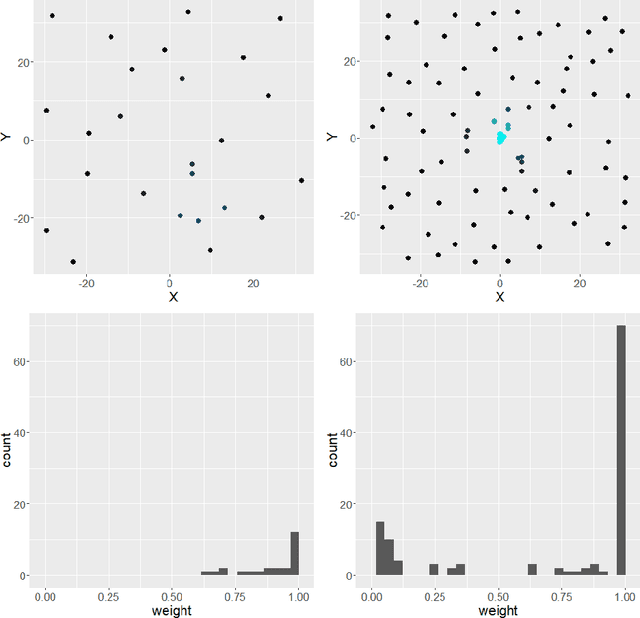
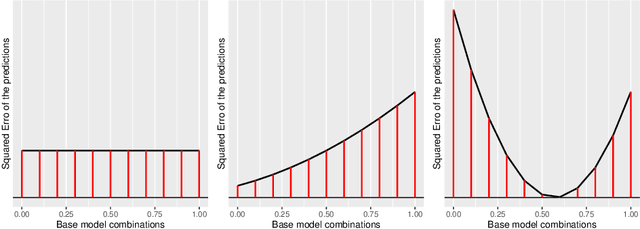
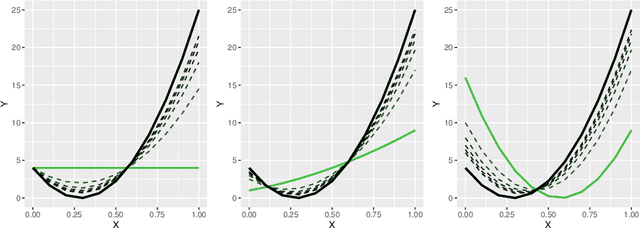
Automated model selection is often proposed to users to choose which machine learning model (or method) to apply to a given regression task. In this paper, we show that combining different regression models can yield better results than selecting a single ('best') regression model, and outline an efficient method that obtains optimally weighted convex linear combination from a heterogeneous set of regression models. More specifically, in this paper, a heuristic weight optimization, used in a preceding conference paper, is replaced by an exact optimization algorithm using convex quadratic programming. We prove convexity of the quadratic programming formulation for the straightforward formulation and for a formulation with weighted data points. The novel weight optimization is not only (more) exact but also more efficient. The methods we develop in this paper are implemented and made available via github-open source. They can be executed on commonly available hardware and offer a transparent and easy to interpret interface. The results indicate that the approach outperforms model selection methods on a range of data sets, including data sets with mixed variable type from drug discovery applications.

Probability Distribution of Hypervolume Improvement in Bi-objective Bayesian Optimization

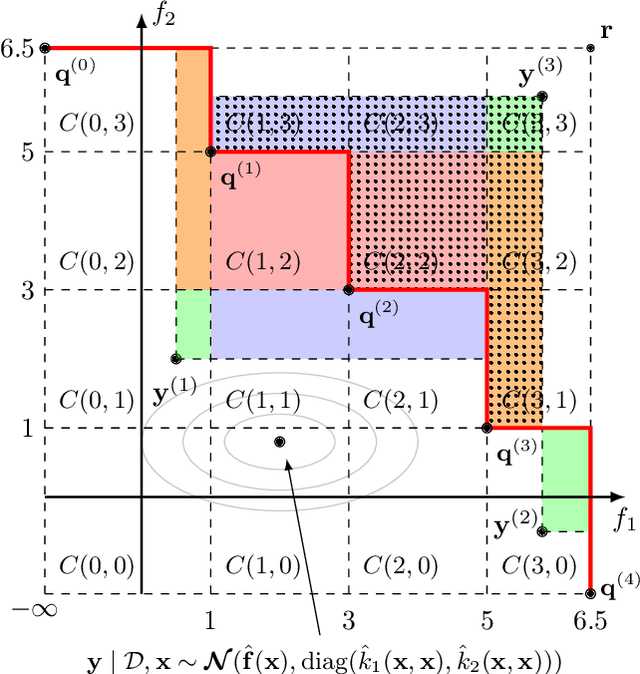
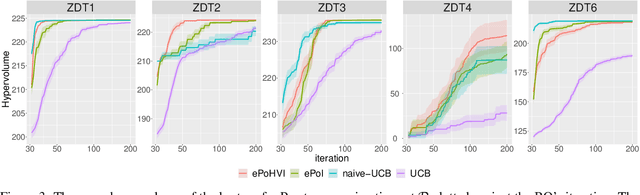
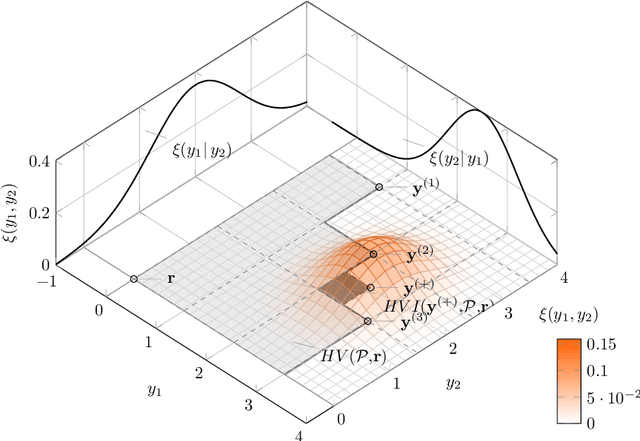
This work provides the exact expression of the probability distribution of the hypervolume improvement (HVI) for bi-objective generalization of Bayesian optimization. Here, instead of a single-objective improvement, we consider the improvement of the hypervolume indicator concerning the current best approximation of the Pareto front. Gaussian process regression models are trained independently on both objective functions, resulting in a bi-variate separated Gaussian distribution serving as a predictive model for the vector-valued objective function. Some commonly HVI-based acquisition functions (probability of improvement and upper confidence bound) are also leveraged with the help of the exact distribution of HVI. In addition, we show the superior numerical accuracy and efficiency of the exact distribution compared to the commonly used approximation by Monte-Carlo sampling. Finally, we benchmark distribution-leveraged acquisition functions on the widely applied ZDT problem set, demonstrating a significant advantage of using the exact distribution of HVI in multi-objective Bayesian optimization.

Automatic Preference Based Multi-objective Evolutionary Algorithm on Vehicle Fleet Maintenance Scheduling Optimization

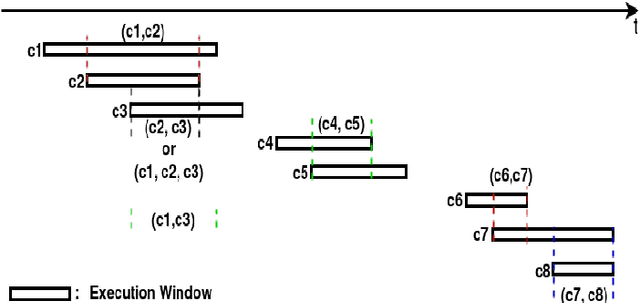
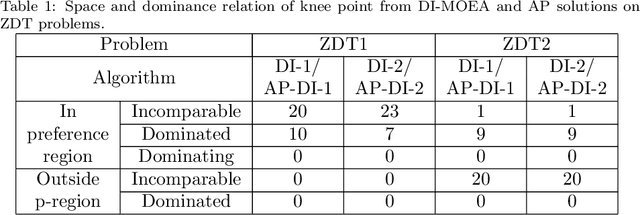
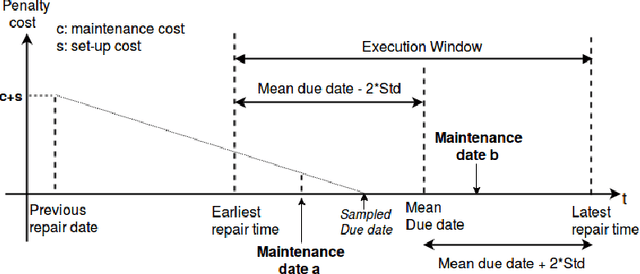
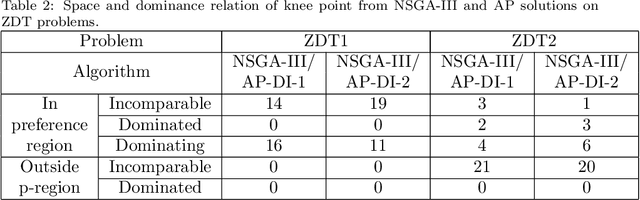
A preference based multi-objective evolutionary algorithm is proposed for generating solutions in an automatically detected knee point region. It is named Automatic Preference based DI-MOEA (AP-DI-MOEA) where DI-MOEA stands for Diversity-Indicator based Multi-Objective Evolutionary Algorithm). AP-DI-MOEA has two main characteristics: firstly, it generates the preference region automatically during the optimization; secondly, it concentrates the solution set in this preference region. Moreover, the real-world vehicle fleet maintenance scheduling optimization (VFMSO) problem is formulated, and a customized multi-objective evolutionary algorithm (MOEA) is proposed to optimize maintenance schedules of vehicle fleets based on the predicted failure distribution of the components of cars. Furthermore, the customized MOEA for VFMSO is combined with AP-DI-MOEA to find maintenance schedules in the automatically generated preference region. Experimental results on multi-objective benchmark problems and our three-objective real-world application problems show that the newly proposed algorithm can generate the preference region accurately and that it can obtain better solutions in the preference region. Especially, in many cases, under the same budget, the Pareto optimal solutions obtained by AP-DI-MOEA dominate solutions obtained by MOEAs that pursue the entire Pareto front.

Multiple Node Immunisation for Preventing Epidemics on Networks by Exact Multiobjective Optimisation of Cost and Shield-Value

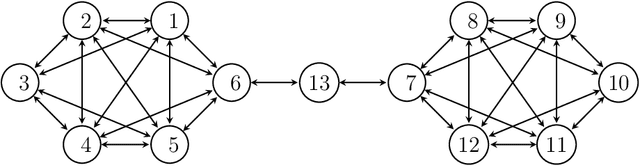
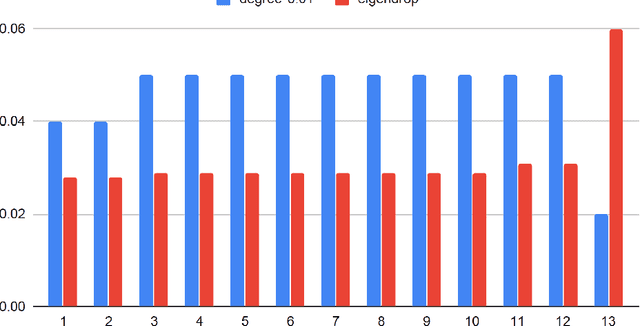
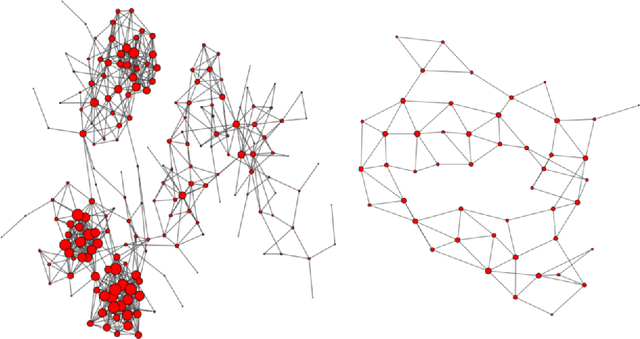
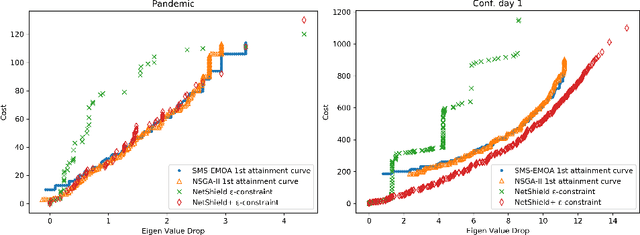
The general problem in this paper is vertex (node) subset selection with the goal to contain an infection that spreads in a network. Instead of selecting the single most important node, this paper deals with the problem of selecting multiple nodes for removal. As compared to previous work on multiple-node selection, the trade-off between cost and benefit is considered. The benefit is measured in terms of increasing the epidemic threshold which is a measure of how difficult it is for an infection to spread in a network. The cost is measured in terms of the number and size of nodes to be removed or controlled. Already in its single-objective instance with a fixed number of $k$ nodes to be removed, the multiple vertex immunisation problems have been proven to be NP-hard. Several heuristics have been developed to approximate the problem. In this work, we compare meta-heuristic techniques with exact methods on the Shield-value, which is a sub-modular proxy for the maximal eigenvalue and used in the current state-of-the-art greedy node-removal strategies. We generalise it to the multi-objective case and replace the greedy algorithm by a quadratic program (QP), which then can be solved with exact QP solvers. The main contribution of this paper is the insight that, if time permits, exact and problem-specific methods approximation should be used, which are often far better than Pareto front approximations obtained by general meta-heuristics. Based on these, it will be more effective to develop strategies for controlling real-world networks when the goal is to prevent or contain epidemic outbreaks. This paper is supported by ready to use Python implementation of the optimization methods and datasets.

Tackling Morpion Solitaire with AlphaZero-likeRanked Reward Reinforcement Learning

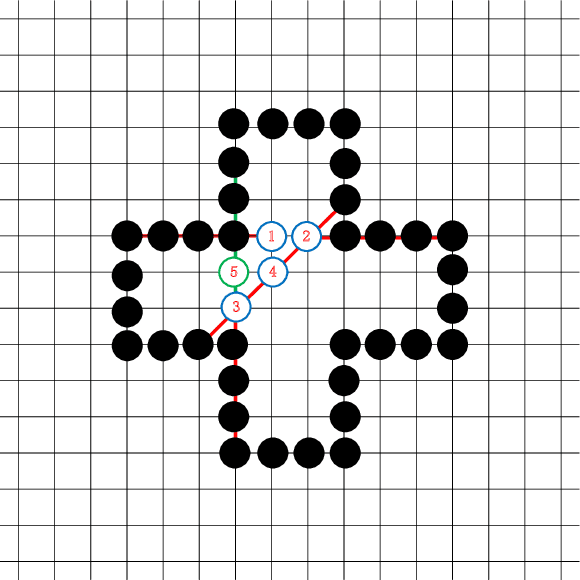
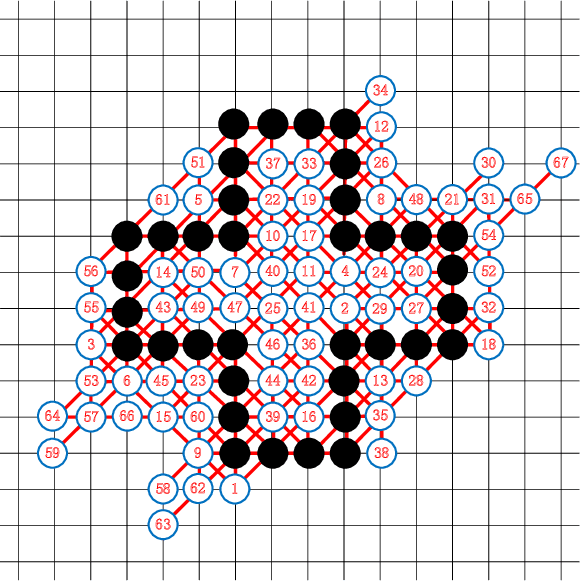
Morpion Solitaire is a popular single player game, performed with paper and pencil. Due to its large state space (on the order of the game of Go) traditional search algorithms, such as MCTS, have not been able to find good solutions. A later algorithm, Nested Rollout Policy Adaptation, was able to find a new record of 82 steps, albeit with large computational resources. After achieving this record, to the best of our knowledge, there has been no further progress reported, for about a decade. In this paper we take the recent impressive performance of deep self-learning reinforcement learning approaches from AlphaGo/AlphaZero as inspiration to design a searcher for Morpion Solitaire. A challenge of Morpion Solitaire is that the state space is sparse, there are few win/loss signals. Instead, we use an approach known as ranked reward to create a reinforcement learning self-play framework for Morpion Solitaire. This enables us to find medium-quality solutions with reasonable computational effort. Our record is a 67 steps solution, which is very close to the human best (68) without any other adaptation to the problem than using ranked reward. We list many further avenues for potential improvement.

A Novel Column Generation Heuristic for Airline Crew Pairing Optimization with Large-scale Complex Flight Networks

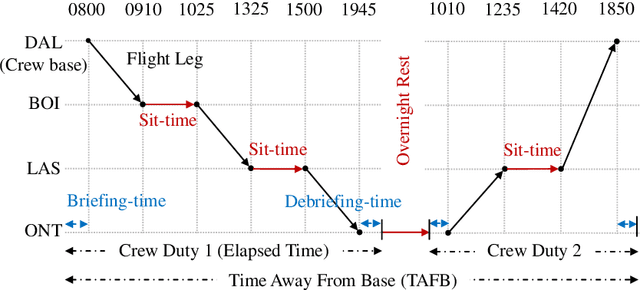
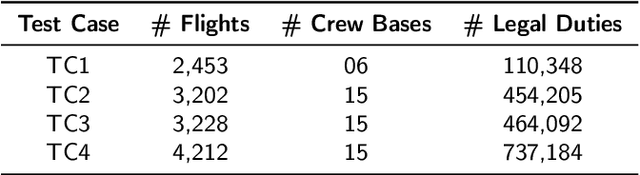
For a large-scale airline, the crew operating cost is second only to the fuel cost. This makes the role of crew pairing optimization (CPO) critical for business viability. Here, the aim is to generate a set of flight sequences (crew pairings) which cover a finite set of an airline's flight schedule, at minimum cost, while satisfying several legality constraints. CPO poses an NP-hard combinatorial optimization problem, to tackle which, the state-of-the-art relies on relaxing the underlying Integer Programming Problem into a Linear Programming Problem, and solving the latter through Column generation (CG) technique. However, with huge expansion of airlines' operations lately, CPO is marred by the curse of dimensionality, rendering the exact CG-implementations obsolete. This has paved the way for use of heuristic-based CG-implementations. Yet, in literature, the much prevalent large-scale complex flight networks involving multiple-crew bases and/or hub-and-spoke sub-networks, largely remain unaddressed. To bridge the research-gap, this paper proposes a novel CG heuristic, which has enabled in-house development of an Airline Crew Pairing Optimizer (AirCROP ). The efficacy of the proposed heuristic/AirCROP has been: (a) tested on real-world airline data with (by available literature) an unprecedented conjunct scale and complexity -- involving over 4200 flights, 15 crew bases, and over a billion pairings, and (b) validated by the research consortium's industrial sponsor. Notably, the proposed CG heuristic relies on balancing exploitation of domain knowledge (on optimal solution features) and random exploration (of solution space). Hence, despite a focused scope here, the proposed CG heuristic can serve as a template on how to utilize domain knowledge for developing heuristics to tackle combinatorial optimization problems in other application domains.

On Initializing Airline Crew Pairing Optimization for Large-scale Complex Flight Networks

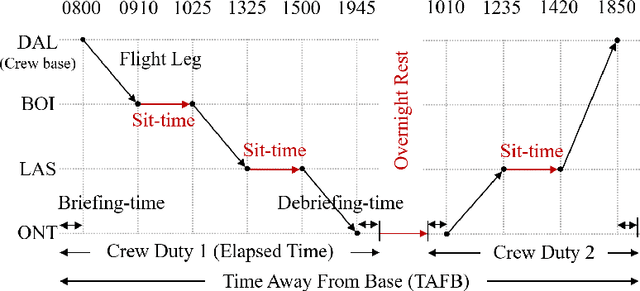
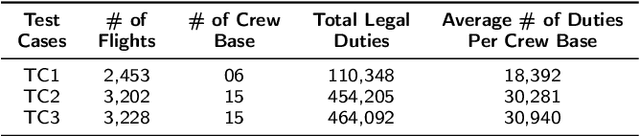
Crew pairing optimization (CPO) is critically important for any airline, since its crew operating costs are second-largest, next to the fuel-cost. CPO aims at generating a set of flight sequences (crew pairings) covering a flight-schedule, at minimum-cost, while satisfying several legality constraints. For large-scale complex flight networks, billion-plus legal pairings (variables) are possible, rendering their offline enumeration intractable and an exhaustive search for their minimum-cost full flight-coverage subset impractical. Even generating an initial feasible solution (IFS: a manageable set of legal pairings covering all flights), which could be subsequently optimized is a difficult (NP-complete) problem. Though, as part of a larger project the authors have developed a crew pairing optimizer (AirCROP), this paper dedicatedly focuses on IFS-generation through a novel heuristic based on divide-and-cover strategy and Integer Programming. For real-world large and complex flight network datasets (including over 3200 flights and 15 crew bases) provided by GE Aviation, the proposed heuristic shows upto a ten-fold speed improvement over another state-of-the-art approach. Unprecedentedly, this paper presents an empirical investigation of the impact of IFS-cost on the final (optimized) solution-cost, revealing that too low an IFS-cost does not necessarily imply faster convergence for AirCROP or even lower cost for the optimized solution.

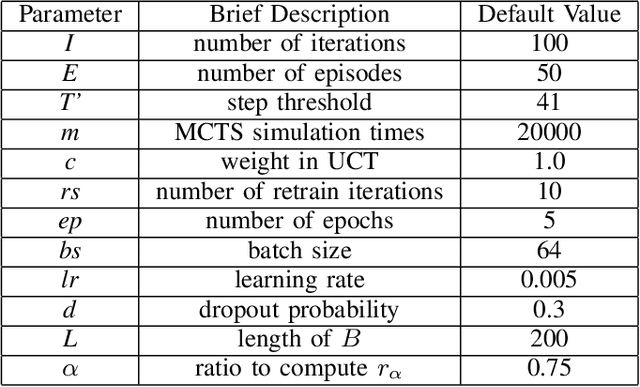
Analysis of Hyper-Parameters for Small Games: Iterations or Epochs in Self-Play?

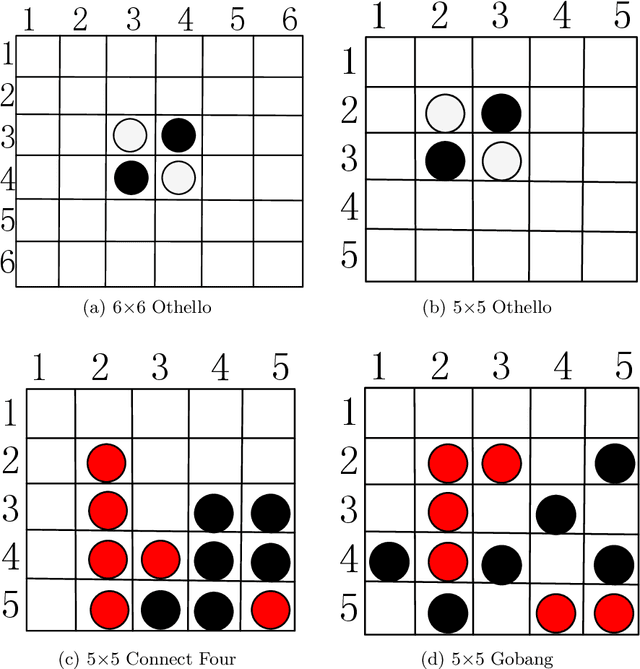
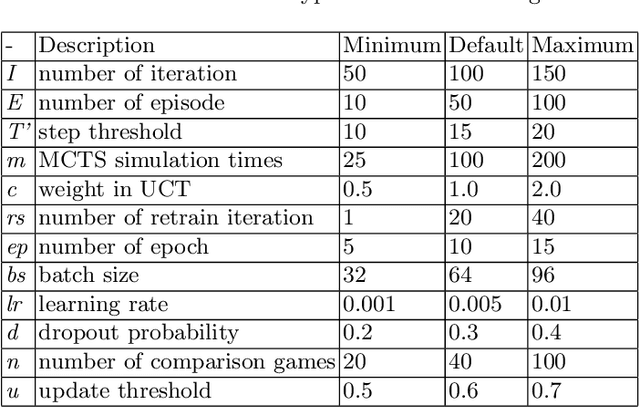
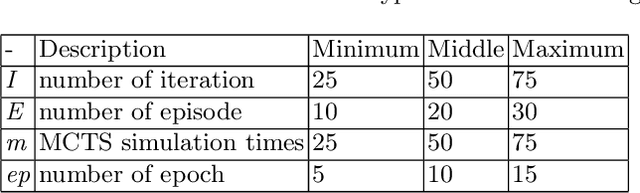
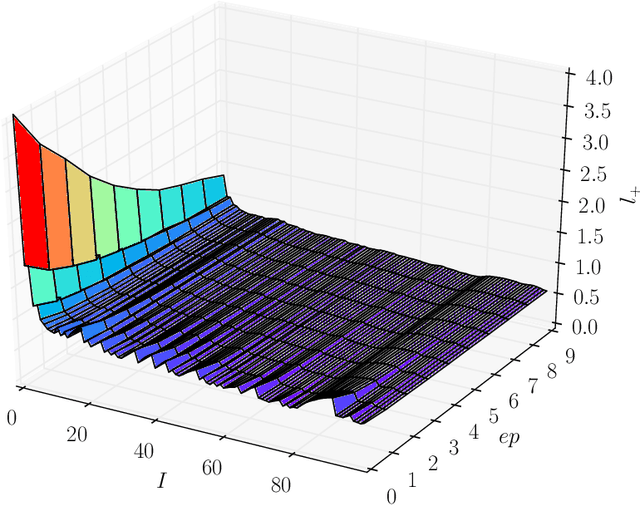
The landmark achievements of AlphaGo Zero have created great research interest into self-play in reinforcement learning. In self-play, Monte Carlo Tree Search is used to train a deep neural network, that is then used in tree searches. Training itself is governed by many hyperparameters.There has been surprisingly little research on design choices for hyper-parameter values and loss-functions, presumably because of the prohibitive computational cost to explore the parameter space. In this paper, we investigate 12 hyper-parameters in an AlphaZero-like self-play algorithm and evaluate how these parameters contribute to training. We use small games, to achieve meaningful exploration with moderate computational effort. The experimental results show that training is highly sensitive to hyper-parameter choices. Through multi-objective analysis we identify 4 important hyper-parameters to further assess. To start, we find surprising results where too much training can sometimes lead to lower performance. Our main result is that the number of self-play iterations subsumes MCTS-search simulations, game-episodes, and training epochs. The intuition is that these three increase together as self-play iterations increase, and that increasing them individually is sub-optimal. A consequence of our experiments is a direct recommendation for setting hyper-parameter values in self-play: the overarching outer-loop of self-play iterations should be maximized, in favor of the three inner-loop hyper-parameters, which should be set at lower values. A secondary result of our experiments concerns the choice of optimization goals, for which we also provide recommendations.

Real-World Airline Crew Pairing Optimization: Customized Genetic Algorithm versus Column Generation Method

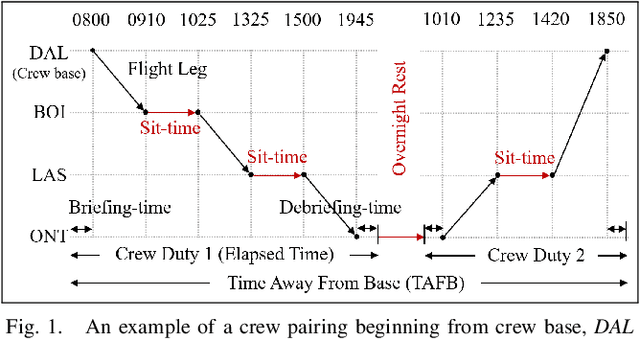
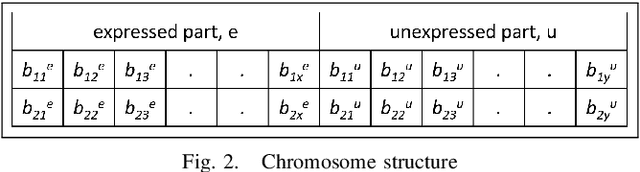
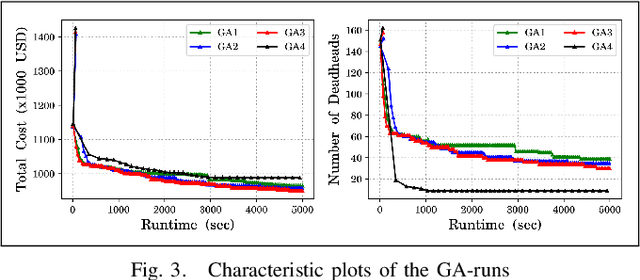
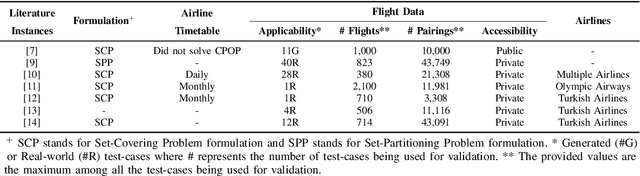
Airline crew cost is the second-largest operating cost component and its marginal improvement may translate to millions of dollars annually. Further, it's highly constrained-combinatorial nature brings-in high impact research and commercial value. The airline crew pairing optimization problem (CPOP) is aimed at generating a set of crew pairings, covering all flights from its timetable, with minimum cost, while satisfying multiple legality constraints laid by federations, etc. Depending upon CPOP's scale, several Genetic Algorithm and Column Generation based approaches have been proposed in the literature. However, these approaches have been validated either on small-scale flight datasets (a handful of pairings) or for smaller airlines (operating-in low-demand regions) such as Turkish Airlines, etc. Their search-efficiency gets impaired drastically when scaled to the networks of bigger airlines. The contributions of this paper relate to the proposition of a customized genetic algorithm, with improved initialization and genetic operators, developed by exploiting the domain-knowledge; and its comparison with a column generation based large-scale optimizer (developed by authors). To demonstrate the utility of the above-cited contributions, a real-world test-case (839 flights), provided by GE Aviation, is used which has been extracted from the networks of larger airlines (operating up to 33000 monthly flights in the US).

Efficient Computation of Expected Hypervolume Improvement Using Box Decomposition Algorithms

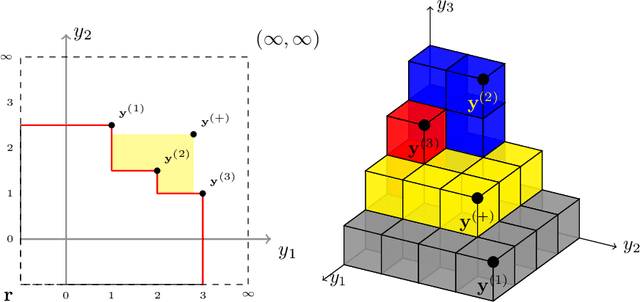
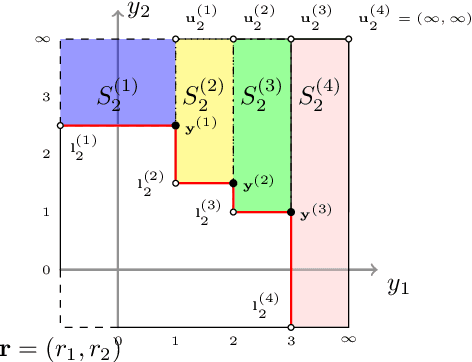
In the field of multi-objective optimization algorithms, multi-objective Bayesian Global Optimization (MOBGO) is an important branch, in addition to evolutionary multi-objective optimization algorithms (EMOAs). MOBGO utilizes Gaussian Process Models learned from previous objective function evaluations to decide the next evaluation site by maximizing or minimizing an infill criterion. A common criterion in MOBGO is the Expected Hypervolume Improvement (EHVI), which shows a good performance on a wide range of problems, with respect to exploration and exploitation. However, so far it has been a challenge to calculate exact EHVI values efficiently. In this paper, an efficient algorithm for the computation of the exact EHVI for a generic case is proposed. This efficient algorithm is based on partitioning the integration volume into a set of axis-parallel slices. Theoretically, the upper bound time complexities are improved from previously $O (n^2)$ and $O(n^3)$, for two- and three-objective problems respectively, to $\Theta(n\log n)$, which is asymptotically optimal. This article generalizes the scheme in higher dimensional case by utilizing a new hyperbox decomposition technique, which was proposed by D{\"a}chert et al, EJOR, 2017. It also utilizes a generalization of the multilayered integration scheme that scales linearly in the number of hyperboxes of the decomposition. The speed comparison shows that the proposed algorithm in this paper significantly reduces computation time. Finally, this decomposition technique is applied in the calculation of the Probability of Improvement (PoI).