Neural-ANOVA: Model Decomposition for Interpretable Machine Learning

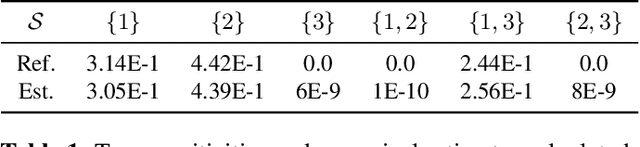
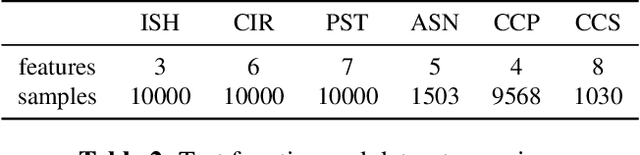
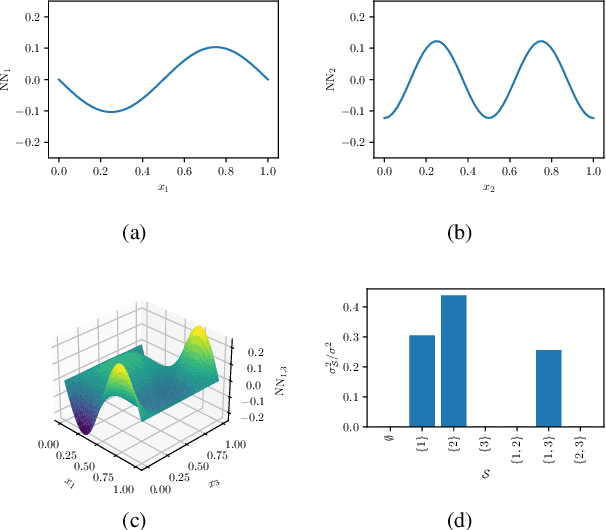
The analysis of variance (ANOVA) decomposition offers a systematic method to understand the interaction effects that contribute to a specific decision output. In this paper we introduce Neural-ANOVA, an approach to decompose neural networks into glassbox models using the ANOVA decomposition. Our approach formulates a learning problem, which enables rapid and closed-form evaluation of integrals over subspaces that appear in the calculation of the ANOVA decomposition. Finally, we conduct numerical experiments to illustrate the advantages of enhanced interpretability and model validation by a decomposition of the learned interaction effects.

The Energy Prediction Smart-Meter Dataset: Analysis of Previous Competitions and Beyond

This paper presents the real-world smart-meter dataset and offers an analysis of solutions derived from the Energy Prediction Technical Challenges, focusing primarily on two key competitions: the IEEE Computational Intelligence Society (IEEE-CIS) Technical Challenge on Energy Prediction from Smart Meter data in 2020 (named EP) and its follow-up challenge at the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE) in 2021 (named as XEP). These competitions focus on accurate energy consumption forecasting and the importance of interpretability in understanding the underlying factors. The challenge aims to predict monthly and yearly estimated consumption for households, addressing the accurate billing problem with limited historical smart meter data. The dataset comprises 3,248 smart meters, with varying data availability ranging from a minimum of one month to a year. This paper delves into the challenges, solutions and analysing issues related to the provided real-world smart meter data, developing accurate predictions at the household level, and introducing evaluation criteria for assessing interpretability. Additionally, this paper discusses aspects beyond the competitions: opportunities for energy disaggregation and pattern detection applications at the household level, significance of communicating energy-driven factors for optimised billing, and emphasising the importance of responsible AI and data privacy considerations. These aspects provide insights into the broader implications and potential advancements in energy consumption prediction. Overall, these competitions provide a dataset for residential energy research and serve as a catalyst for exploring accurate forecasting, enhancing interpretability, and driving progress towards the discussion of various aspects such as energy disaggregation, demand response programs or behavioural interventions.

Comparison and Evaluation of Methods for a Predict+Optimize Problem in Renewable Energy

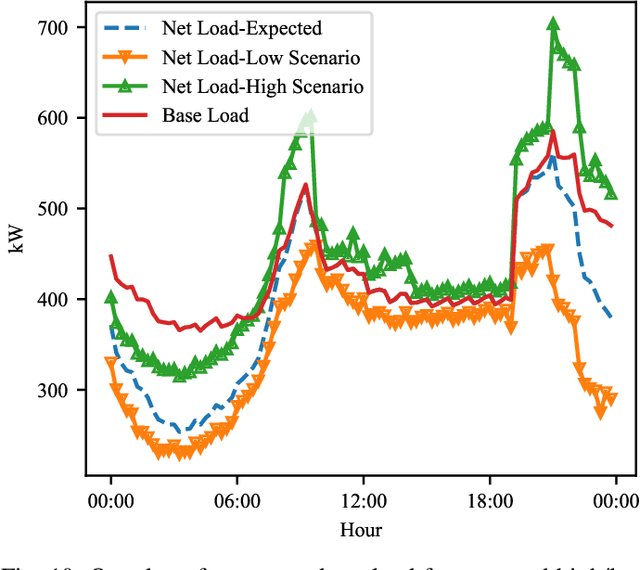
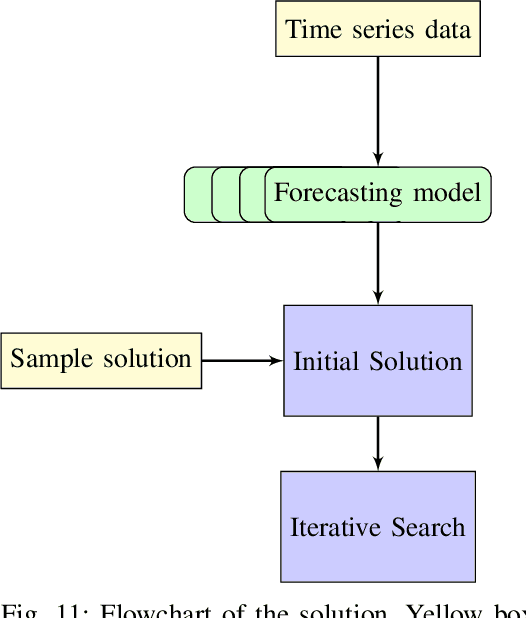
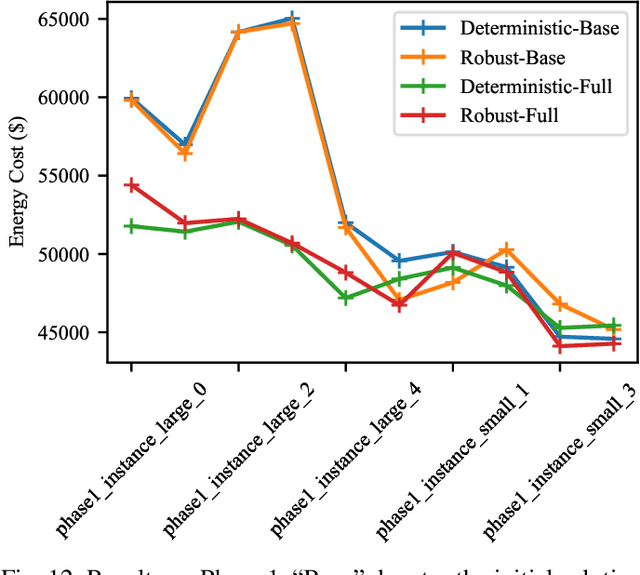
Algorithms that involve both forecasting and optimization are at the core of solutions to many difficult real-world problems, such as in supply chains (inventory optimization), traffic, and in the transition towards carbon-free energy generation in battery/load/production scheduling in sustainable energy systems. Typically, in these scenarios we want to solve an optimization problem that depends on unknown future values, which therefore need to be forecast. As both forecasting and optimization are difficult problems in their own right, relatively few research has been done in this area. This paper presents the findings of the ``IEEE-CIS Technical Challenge on Predict+Optimize for Renewable Energy Scheduling," held in 2021. We present a comparison and evaluation of the seven highest-ranked solutions in the competition, to provide researchers with a benchmark problem and to establish the state of the art for this benchmark, with the aim to foster and facilitate research in this area. The competition used data from the Monash Microgrid, as well as weather data and energy market data. It then focused on two main challenges: forecasting renewable energy production and demand, and obtaining an optimal schedule for the activities (lectures) and on-site batteries that lead to the lowest cost of energy. The most accurate forecasts were obtained by gradient-boosted tree and random forest models, and optimization was mostly performed using mixed integer linear and quadratic programming. The winning method predicted different scenarios and optimized over all scenarios jointly using a sample average approximation method.

Physics-informed neural networks for pathloss prediction

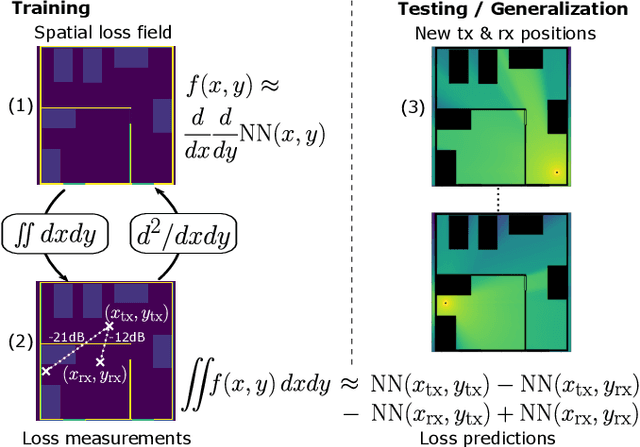
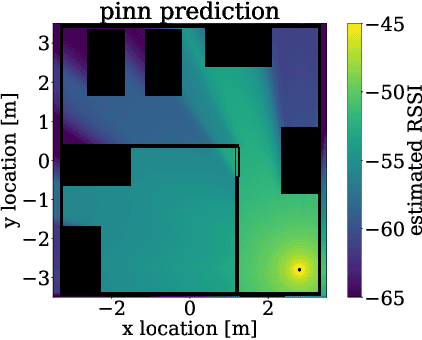
This paper introduces a physics-informed machine learning approach for pathloss prediction. This is achieved by including in the training phase simultaneously (i) physical dependencies between spatial loss field and (ii) measured pathloss values in the field. It is shown that the solution to a proposed learning problem improves generalization and prediction quality with a small number of neural network layers and parameters. The latter leads to fast inference times which are favorable for downstream tasks such as localization. Moreover, the physics-informed formulation allows training and prediction with small amount of training data which makes it appealing for a wide range of practical pathloss prediction scenarios.

Automatic Preference Based Multi-objective Evolutionary Algorithm on Vehicle Fleet Maintenance Scheduling Optimization

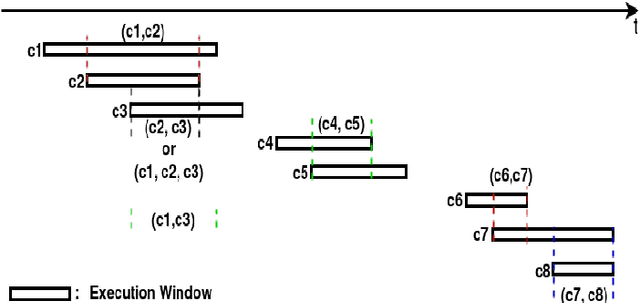
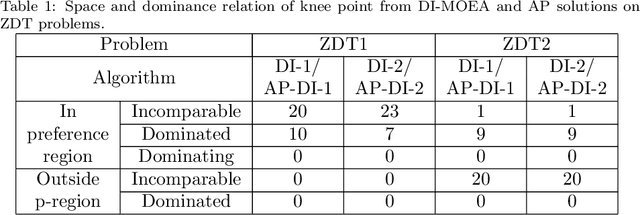
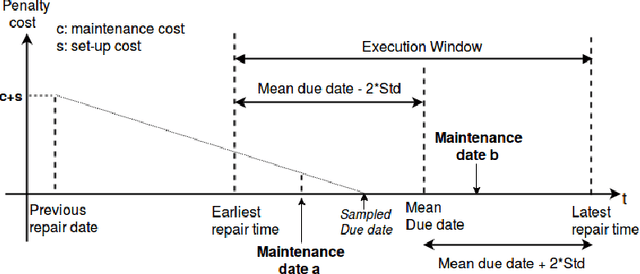
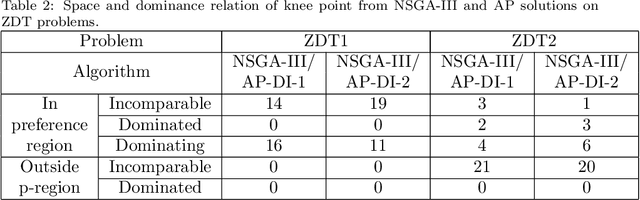
A preference based multi-objective evolutionary algorithm is proposed for generating solutions in an automatically detected knee point region. It is named Automatic Preference based DI-MOEA (AP-DI-MOEA) where DI-MOEA stands for Diversity-Indicator based Multi-Objective Evolutionary Algorithm). AP-DI-MOEA has two main characteristics: firstly, it generates the preference region automatically during the optimization; secondly, it concentrates the solution set in this preference region. Moreover, the real-world vehicle fleet maintenance scheduling optimization (VFMSO) problem is formulated, and a customized multi-objective evolutionary algorithm (MOEA) is proposed to optimize maintenance schedules of vehicle fleets based on the predicted failure distribution of the components of cars. Furthermore, the customized MOEA for VFMSO is combined with AP-DI-MOEA to find maintenance schedules in the automatically generated preference region. Experimental results on multi-objective benchmark problems and our three-objective real-world application problems show that the newly proposed algorithm can generate the preference region accurately and that it can obtain better solutions in the preference region. Especially, in many cases, under the same budget, the Pareto optimal solutions obtained by AP-DI-MOEA dominate solutions obtained by MOEAs that pursue the entire Pareto front.

Interpretable Control by Reinforcement Learning

In this paper, three recently introduced reinforcement learning (RL) methods are used to generate human-interpretable policies for the cart-pole balancing benchmark. The novel RL methods learn human-interpretable policies in the form of compact fuzzy controllers and simple algebraic equations. The representations as well as the achieved control performances are compared with two classical controller design methods and three non-interpretable RL methods. All eight methods utilize the same previously generated data batch and produce their controller offline - without interaction with the real benchmark dynamics. The experiments show that the novel RL methods are able to automatically generate well-performing policies which are at the same time human-interpretable. Furthermore, one of the methods is applied to automatically learn an equation-based policy for a hardware cart-pole demonstrator by using only human-player-generated batch data. The solution generated in the first attempt already represents a successful balancing policy, which demonstrates the methods applicability to real-world problems.

Optimal deep neural networks for sparse recovery via Laplace techniques

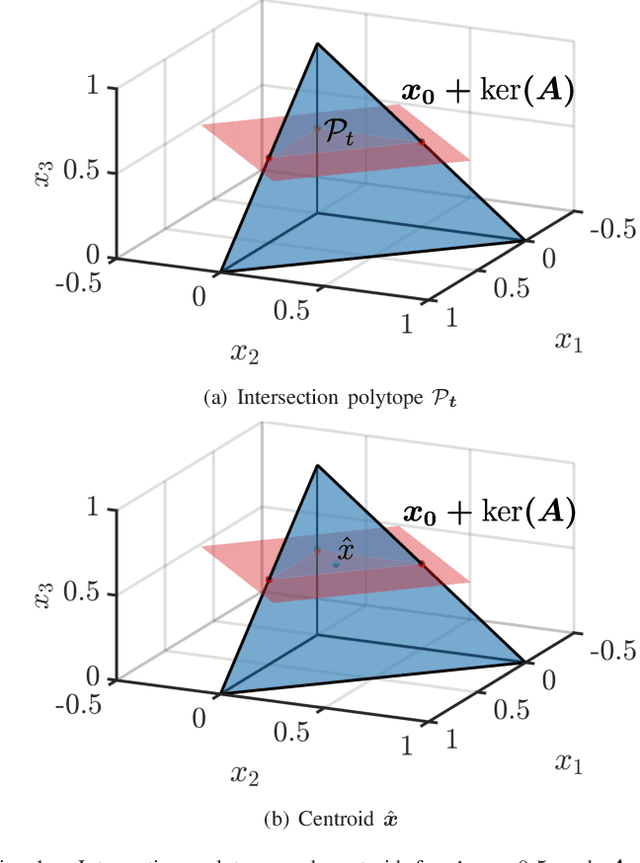
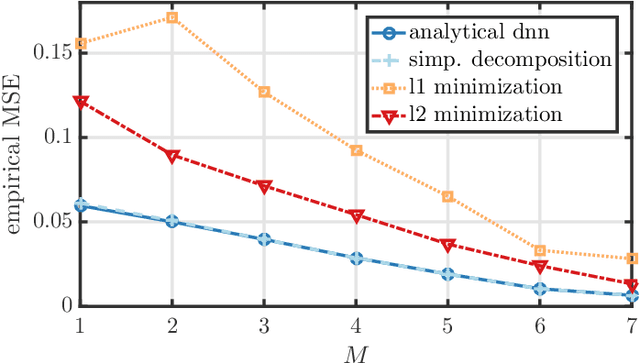
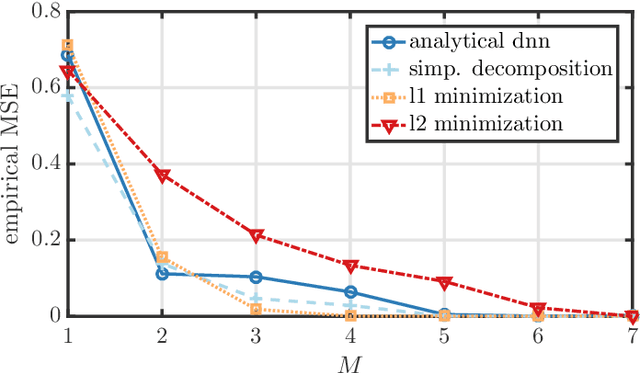
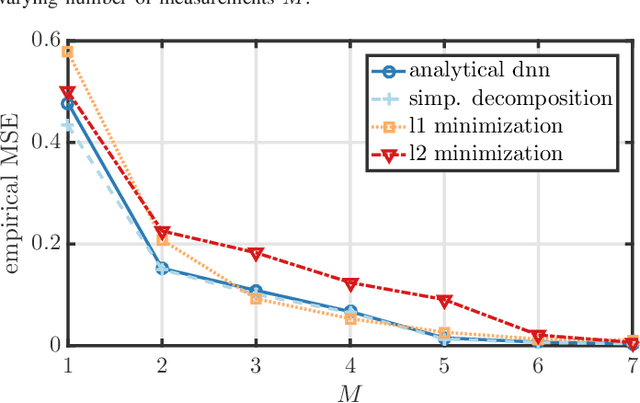
This paper introduces Laplace techniques for designing a neural network, with the goal of estimating simplex-constraint sparse vectors from compressed measurements. To this end, we recast the problem of MMSE estimation (w.r.t. a pre-defined uniform input distribution) as the problem of computing the centroid of some polytope that results from the intersection of the simplex and an affine subspace determined by the measurements. Owing to the specific structure, it is shown that the centroid can be computed analytically by extending a recent result that facilitates the volume computation of polytopes via Laplace transformations. A main insight of this paper is that the desired volume and centroid computations can be performed by a classical deep neural network comprising threshold functions, rectified linear (ReLU) and rectified polynomial (ReP) activation functions. The proposed construction of a deep neural network for sparse recovery is completely analytic so that time-consuming training procedures are not necessary. Furthermore, we show that the number of layers in our construction is equal to the number of measurements which might enable novel low-latency sparse recovery algorithms for a larger class of signals than that assumed in this paper. To assess the applicability of the proposed uniform input distribution, we showcase the recovery performance on samples that are soft-classification vectors generated by two standard datasets. As both volume and centroid computation are known to be computationally hard, the network width grows exponentially in the worst-case. It can be, however, decreased by inducing sparse connectivity in the neural network via a well-suited basis of the affine subspace. Finally, the presented analytical construction may serve as a viable initialization to be further optimized and trained using particular input datasets at hand.

Towards optimal nonlinearities for sparse recovery using higher-order statistics

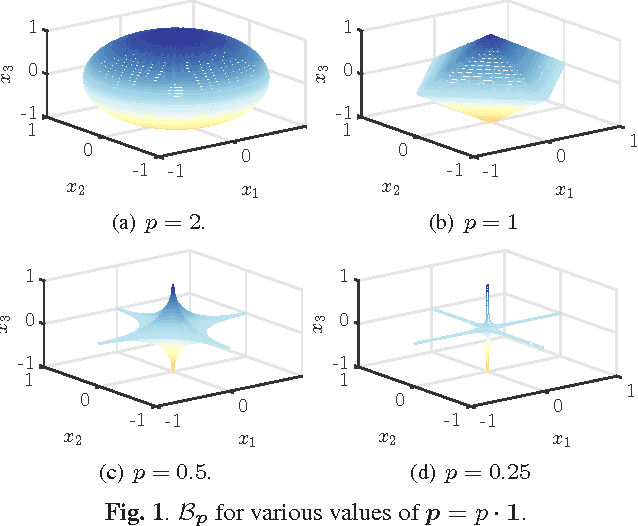
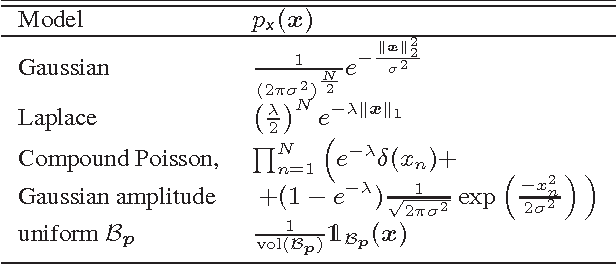
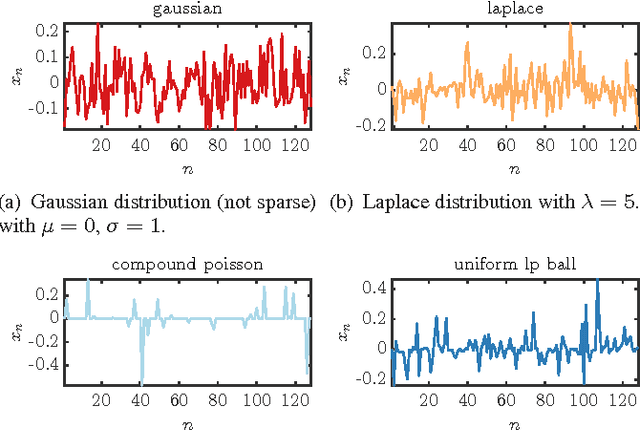
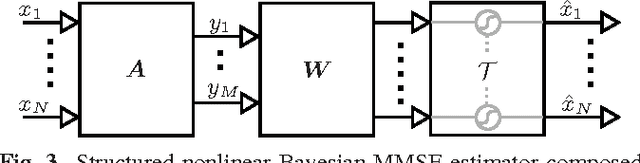
We consider machine learning techniques to develop low-latency approximate solutions to a class of inverse problems. More precisely, we use a probabilistic approach for the problem of recovering sparse stochastic signals that are members of the $\ell_p$-balls. In this context, we analyze the Bayesian mean-square-error (MSE) for two types of estimators: (i) a linear estimator and (ii) a structured estimator composed of a linear operator followed by a Cartesian product of univariate nonlinear mappings. By construction, the complexity of the proposed nonlinear estimator is comparable to that of its linear counterpart since the nonlinear mapping can be implemented efficiently in hardware by means of look-up tables (LUTs). The proposed structure lends itself to neural networks and iterative shrinkage/thresholding-type algorithms restricted to a single iterate (e.g. due to imposed hardware or latency constraints). By resorting to an alternating minimization technique, we obtain a sequence of optimized linear operators and nonlinear mappings that converge in the MSE objective. The result is attractive for real-time applications where general iterative and convex optimization methods are infeasible.