A Real-World Energy Management Dataset from a Smart Company Building for Optimization and Machine Learning

We present a large real-world dataset obtained from monitoring a smart company facility over the course of six years, from 2018 to 2023. The dataset includes energy consumption data from various facility areas and components, energy production data from a photovoltaic system and a combined heat and power plant, operational data from heating and cooling systems, and weather data from an on-site weather station. The measurement sensors installed throughout the facility are organized in a hierarchical metering structure with multiple sub-metering levels, which is reflected in the dataset. The dataset contains measurement data from 72 energy meters, 9 heat meters and a weather station. Both raw and processed data at different processing levels, including labeled issues, is available. In this paper, we describe the data acquisition and post-processing employed to create the dataset. The dataset enables the application of a wide range of methods in the domain of energy management, including optimization, modeling, and machine learning to optimize building operations and reduce costs and carbon emissions.

Precision and Recall Reject Curves for Classification

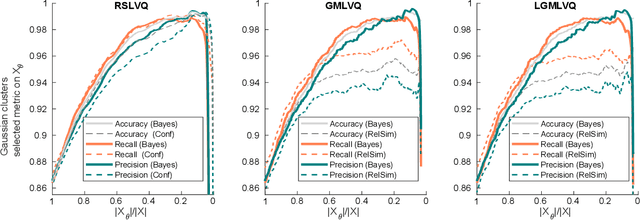
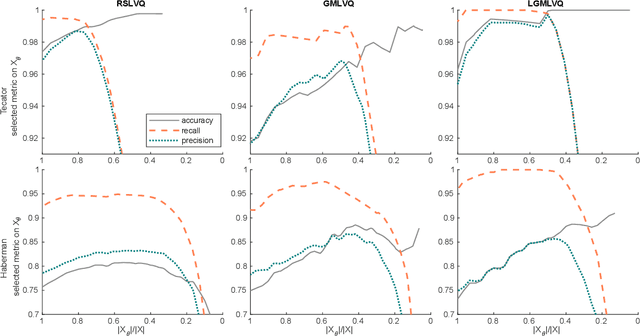
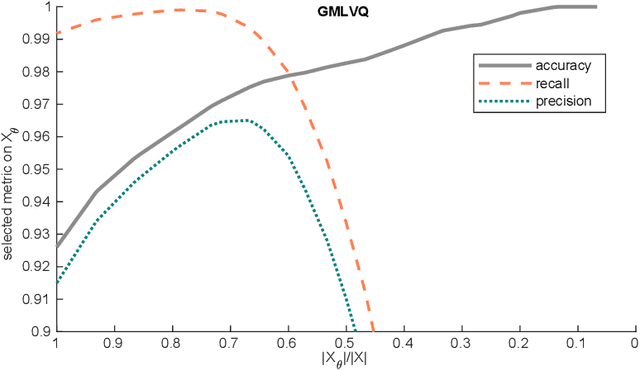
For some classification scenarios, it is desirable to use only those classification instances that a trained model associates with a high certainty. To obtain such high-certainty instances, previous work has proposed accuracy-reject curves. Reject curves allow to evaluate and compare the performance of different certainty measures over a range of thresholds for accepting or rejecting classifications. However, the accuracy may not be the most suited evaluation metric for all applications, and instead precision or recall may be preferable. This is the case, for example, for data with imbalanced class distributions. We therefore propose reject curves that evaluate precision and recall, the recall-reject curve and the precision-reject curve. Using prototype-based classifiers from learning vector quantization, we first validate the proposed curves on artificial benchmark data against the accuracy reject curve as a baseline. We then show on imbalanced benchmarks and medical, real-world data that for these scenarios, the proposed precision- and recall-curves yield more accurate insights into classifier performance than accuracy reject curves.

Understanding Concept Identification as Consistent Data Clustering Across Multiple Feature Spaces

Identifying meaningful concepts in large data sets can provide valuable insights into engineering design problems. Concept identification aims at identifying non-overlapping groups of design instances that are similar in a joint space of all features, but which are also similar when considering only subsets of features. These subsets usually comprise features that characterize a design with respect to one specific context, for example, constructive design parameters, performance values, or operation modes. It is desirable to evaluate the quality of design concepts by considering several of these feature subsets in isolation. In particular, meaningful concepts should not only identify dense, well separated groups of data instances, but also provide non-overlapping groups of data that persist when considering pre-defined feature subsets separately. In this work, we propose to view concept identification as a special form of clustering algorithm with a broad range of potential applications beyond engineering design. To illustrate the differences between concept identification and classical clustering algorithms, we apply a recently proposed concept identification algorithm to two synthetic data sets and show the differences in identified solutions. In addition, we introduce the mutual information measure as a metric to evaluate whether solutions return consistent clusters across relevant subsets. To support the novel understanding of concept identification, we consider a simulated data set from a decision-making problem in the energy management domain and show that the identified clusters are more interpretable with respect to relevant feature subsets than clusters found by common clustering algorithms and are thus more suitable to support a decision maker.

Interaction-Aware Sensitivity Analysis for Aerodynamic Optimization Results using Information Theory

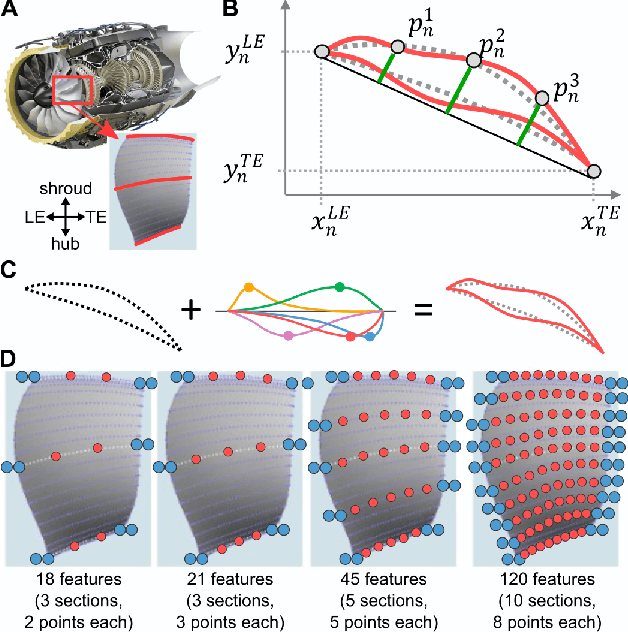
An important issue during an engineering design process is to develop an understanding which design parameters have the most influence on the performance. Especially in the context of optimization approaches this knowledge is crucial in order to realize an efficient design process and achieve high-performing results. Information theory provides powerful tools to investigate these relationships because measures are model-free and thus also capture non-linear relationships, while requiring only minimal assumptions on the input data. We therefore propose to use recently introduced information-theoretic methods and estimation algorithms to find the most influential input parameters in optimization results. The proposed methods are in particular able to account for interactions between parameters, which are often neglected but may lead to redundant or synergistic contributions of multiple parameters. We demonstrate the application of these methods on optimization data from aerospace engineering, where we first identify the most relevant optimization parameters using a recently introduced information-theoretic feature-selection algorithm that accounts for interactions between parameters. Second, we use the novel partial information decomposition (PID) framework that allows to quantify redundant and synergistic contributions between selected parameters with respect to the optimization outcome to identify parameter interactions. We thus demonstrate the power of novel information-theoretic approaches in identifying relevant parameters in optimization runs and highlight how these methods avoid the selection of redundant parameters, while detecting interactions that result in synergistic contributions of multiple parameters.

A Rigorous Information-Theoretic Definition of Redundancy and Relevancy in Feature Selection Based on (Partial) Information Decomposition

Selecting a minimal feature set that is maximally informative about a target variable is a central task in machine learning and statistics. Information theory provides a powerful framework for formulating feature selection algorithms -- yet, a rigorous, information-theoretic definition of feature relevancy, which accounts for feature interactions such as redundant and synergistic contributions, is still missing. We argue that this lack is inherent to classical information theory which does not provide measures to decompose the information a set of variables provides about a target into unique, redundant, and synergistic contributions. Such a decomposition has been introduced only recently by the partial information decomposition (PID) framework. Using PID, we clarify why feature selection is a conceptually difficult problem when approached using information theory and provide a novel definition of feature relevancy and redundancy in PID terms. From this definition, we show that the conditional mutual information (CMI) maximizes relevancy while minimizing redundancy and propose an iterative, CMI-based algorithm for practical feature selection. We demonstrate the power of our CMI-based algorithm in comparison to the unconditional mutual information on benchmark examples and provide corresponding PID estimates to highlight how PID allows to quantify information contribution of features and their interactions in feature-selection problems.

A Compact Spectral Descriptor for Shape Deformations

Modern product design in the engineering domain is increasingly driven by computational analysis including finite-element based simulation, computational optimization, and modern data analysis techniques such as machine learning. To apply these methods, suitable data representations for components under development as well as for related design criteria have to be found. While a component's geometry is typically represented by a polygon surface mesh, it is often not clear how to parametrize critical design properties in order to enable efficient computational analysis. In the present work, we propose a novel methodology to obtain a parameterization of a component's plastic deformation behavior under stress, which is an important design criterion in many application domains, for example, when optimizing the crash behavior in the automotive context. Existing parameterizations limit computational analysis to relatively simple deformations and typically require extensive input by an expert, making the design process time intensive and costly. Hence, we propose a way to derive a compact descriptor of deformation behavior that is based on spectral mesh processing and enables a low-dimensional representation of also complex deformations.We demonstrate the descriptor's ability to represent relevant deformation behavior by applying it in a nearest-neighbor search to identify similar simulation results in a filtering task. The proposed descriptor provides a novel approach to the parametrization of geometric deformation behavior and enables the use of state-of-the-art data analysis techniques such as machine learning to engineering tasks concerned with plastic deformation behavior.