Neural-ANOVA: Model Decomposition for Interpretable Machine Learning

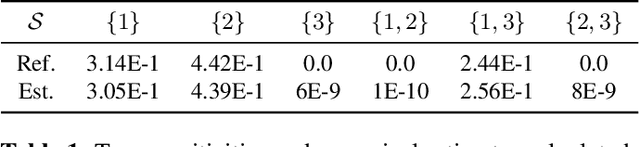
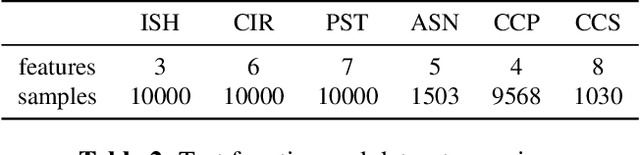
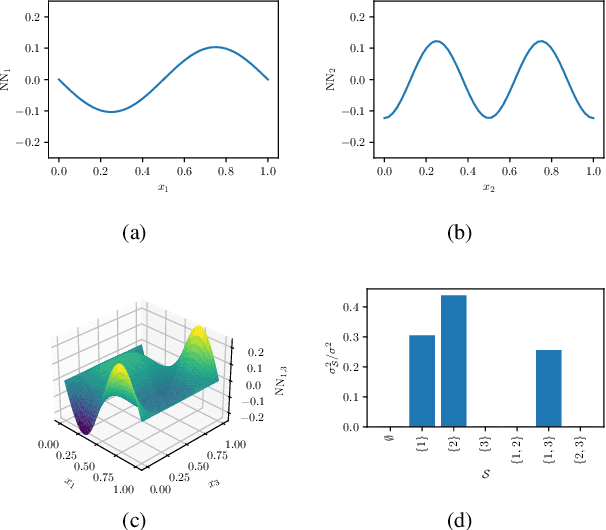
The analysis of variance (ANOVA) decomposition offers a systematic method to understand the interaction effects that contribute to a specific decision output. In this paper we introduce Neural-ANOVA, an approach to decompose neural networks into glassbox models using the ANOVA decomposition. Our approach formulates a learning problem, which enables rapid and closed-form evaluation of integrals over subspaces that appear in the calculation of the ANOVA decomposition. Finally, we conduct numerical experiments to illustrate the advantages of enhanced interpretability and model validation by a decomposition of the learned interaction effects.