Comparative Analysis of Indicators for Multiobjective Diversity Optimization

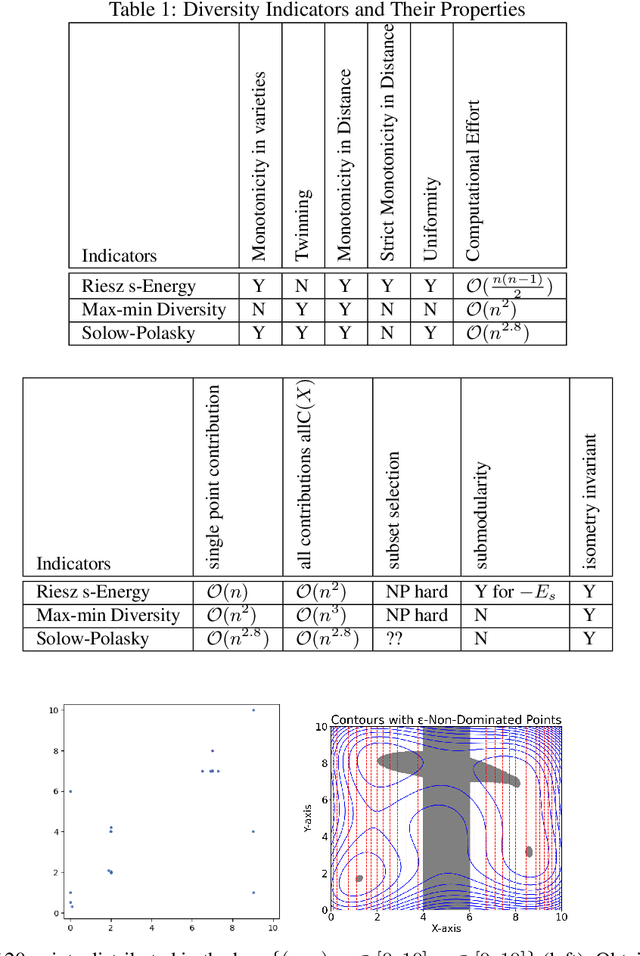
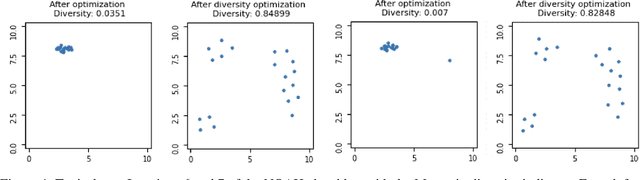
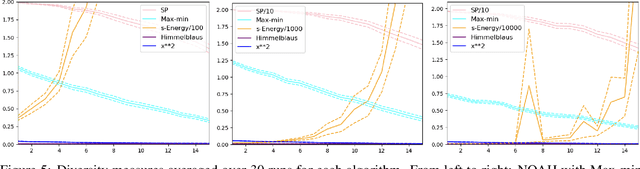
Indicator-based (multiobjective) diversity optimization aims at finding a set of near (Pareto-)optimal solutions that maximizes a diversity indicator, where diversity is typically interpreted as the number of essentially different solutions. Whereas, in the first diversity-oriented evolutionary multiobjective optimization algorithm, the NOAH algorithm by Ulrich and Thiele, the Solow Polasky Diversity (also related to Magnitude) served as a metric, other diversity indicators might be considered, such as the parameter-free Max-Min Diversity, and the Riesz s-Energy, which features uniformly distributed solution sets. In this paper, focusing on multiobjective diversity optimization, we discuss different diversity indicators from the perspective of indicator-based evolutionary algorithms (IBEA) with multiple objectives. We examine theoretical, computational, and practical properties of these indicators, such as monotonicity in species, twinning, monotonicity in distance, strict monotonicity in distance, uniformity of maximizing point sets, computational effort for a set of size~n, single-point contributions, subset selection, and submodularity. We present new theorems -- including a proof of the NP-hardness of the Riesz s-Energy Subset Selection Problem -- and consolidate existing results from the literature. In the second part, we apply these indicators in the NOAH algorithm and analyze search dynamics through an example. We examine how optimizing with one indicator affects the performance of others and propose NOAH adaptations specific to the Max-Min indicator.

A Newton Method for Hausdorff Approximations of the Pareto Front within Multi-objective Evolutionary Algorithms

A common goal in evolutionary multi-objective optimization is to find suitable finite-size approximations of the Pareto front of a given multi-objective optimization problem. While many multi-objective evolutionary algorithms have proven to be very efficient in finding good Pareto front approximations, they may need quite a few resources or may even fail to obtain optimal or nearly approximations. Hereby, optimality is implicitly defined by the chosen performance indicator. In this work, we propose a set-based Newton method for Hausdorff approximations of the Pareto front to be used within multi-objective evolutionary algorithms. To this end, we first generalize the previously proposed Newton step for the performance indicator for the treatment of constrained problems for general reference sets. To approximate the target Pareto front, we propose a particular strategy for generating the reference set that utilizes the data gathered by the evolutionary algorithm during its run. Finally, we show the benefit of the Newton method as a post-processing step on several benchmark test functions and different base evolutionary algorithms.

Improving Many-objective Evolutionary Algorithms by Means of Expanded Cone Orders

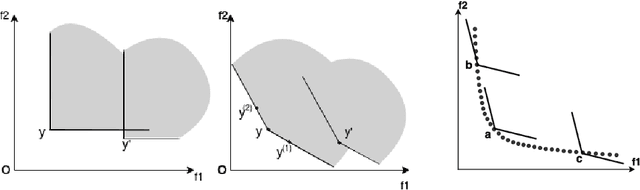
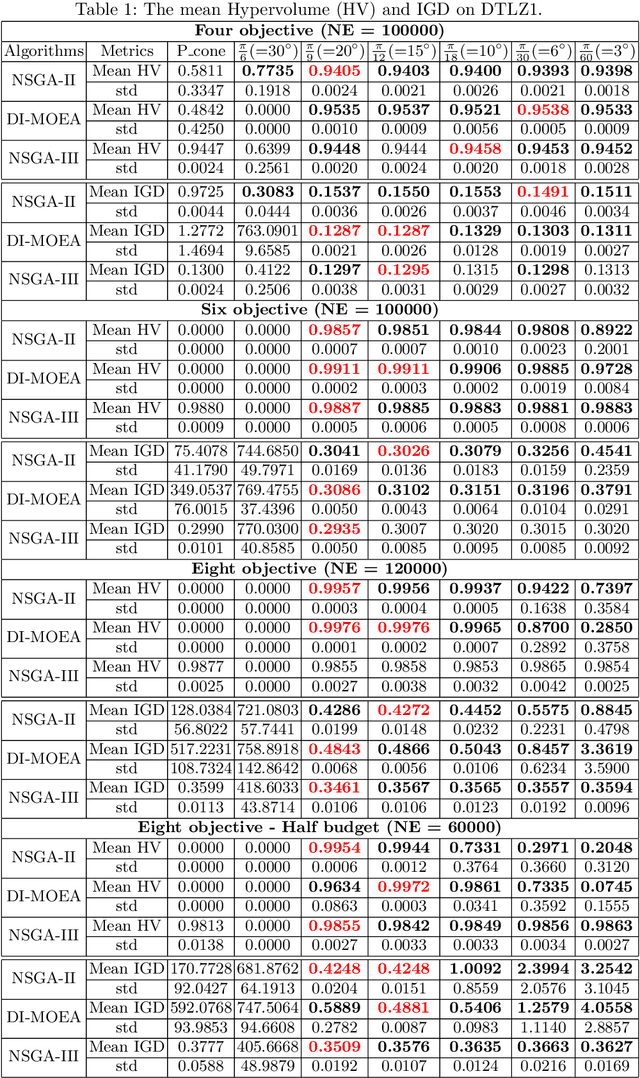
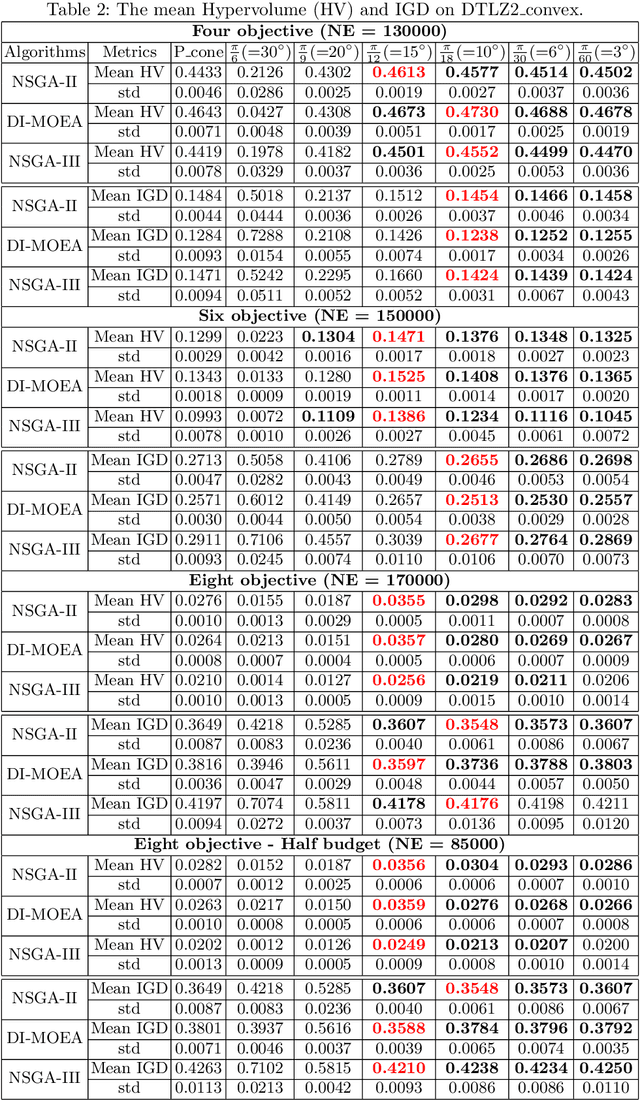
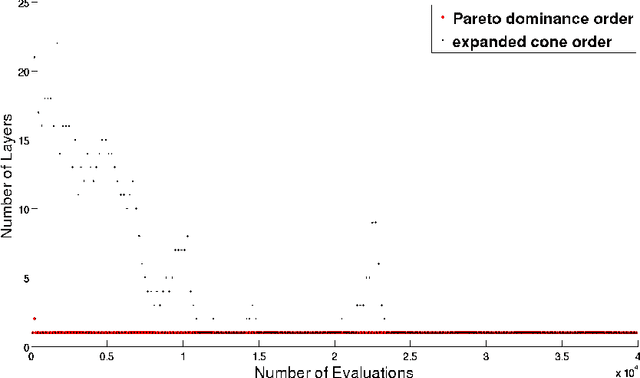
Given a point in m-dimensional objective space, the local environment of a point can be partitioned into the incomparable, the dominated and the dominating region. The ratio between the size of the incomparable region, and the dominated (and dominating) decreases proportionally to $1/2^{m-1}$. Due to this reason, it gets increasingly unlikely that dominating points can be found by random, isotropic mutations. As a remedy to stagnation of search in many objective optimization, in this paper, we suggest to enhance the Pareto dominance order by involving a convex obtuse dominance cone in the convergence phase of an evolutionary optimization algorithm. The approach is integrated in several state-of-the-art multi-objective evolutionary algorithms (MOEAs) and tested on benchmark problems with four, five, six and eight objectives. Computational experiments demonstrate the ability of the expanded cone technique to improve the performance of MOEAs on many-objective optimization problems.

Efficient Computation of Expected Hypervolume Improvement Using Box Decomposition Algorithms

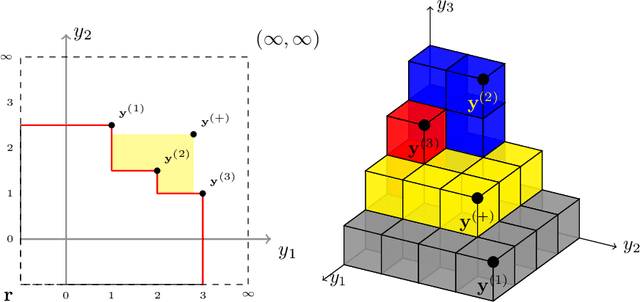
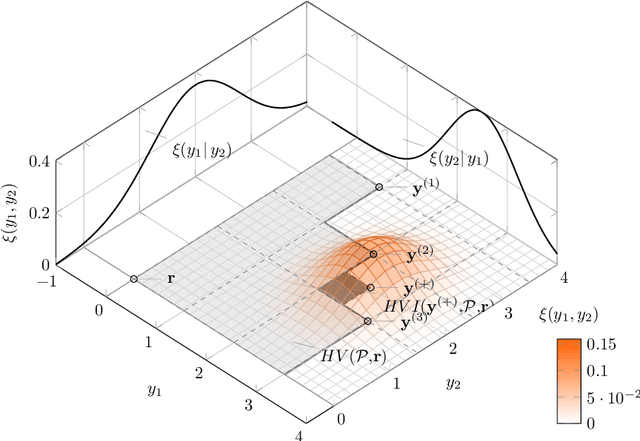
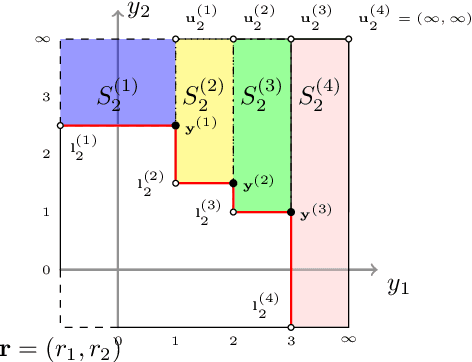
In the field of multi-objective optimization algorithms, multi-objective Bayesian Global Optimization (MOBGO) is an important branch, in addition to evolutionary multi-objective optimization algorithms (EMOAs). MOBGO utilizes Gaussian Process Models learned from previous objective function evaluations to decide the next evaluation site by maximizing or minimizing an infill criterion. A common criterion in MOBGO is the Expected Hypervolume Improvement (EHVI), which shows a good performance on a wide range of problems, with respect to exploration and exploitation. However, so far it has been a challenge to calculate exact EHVI values efficiently. In this paper, an efficient algorithm for the computation of the exact EHVI for a generic case is proposed. This efficient algorithm is based on partitioning the integration volume into a set of axis-parallel slices. Theoretically, the upper bound time complexities are improved from previously $O (n^2)$ and $O(n^3)$, for two- and three-objective problems respectively, to $\Theta(n\log n)$, which is asymptotically optimal. This article generalizes the scheme in higher dimensional case by utilizing a new hyperbox decomposition technique, which was proposed by D{\"a}chert et al, EJOR, 2017. It also utilizes a generalization of the multilayered integration scheme that scales linearly in the number of hyperboxes of the decomposition. The speed comparison shows that the proposed algorithm in this paper significantly reduces computation time. Finally, this decomposition technique is applied in the calculation of the Probability of Improvement (PoI).