Comparative Analysis of Indicators for Multiobjective Diversity Optimization

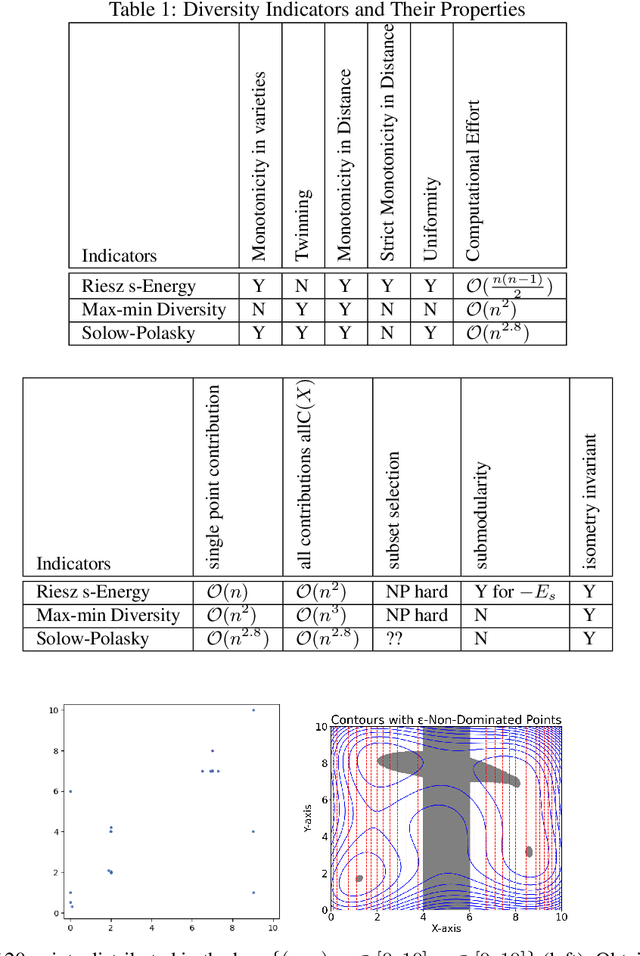
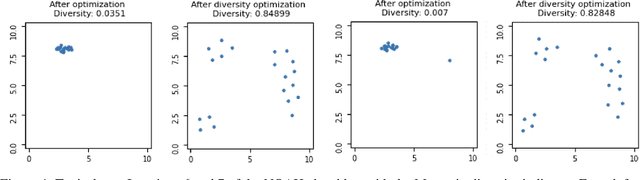
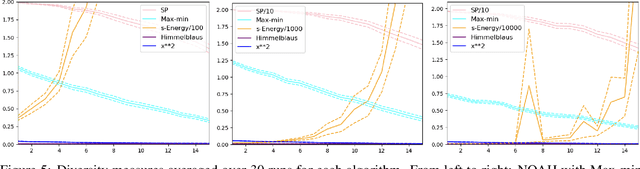
Indicator-based (multiobjective) diversity optimization aims at finding a set of near (Pareto-)optimal solutions that maximizes a diversity indicator, where diversity is typically interpreted as the number of essentially different solutions. Whereas, in the first diversity-oriented evolutionary multiobjective optimization algorithm, the NOAH algorithm by Ulrich and Thiele, the Solow Polasky Diversity (also related to Magnitude) served as a metric, other diversity indicators might be considered, such as the parameter-free Max-Min Diversity, and the Riesz s-Energy, which features uniformly distributed solution sets. In this paper, focusing on multiobjective diversity optimization, we discuss different diversity indicators from the perspective of indicator-based evolutionary algorithms (IBEA) with multiple objectives. We examine theoretical, computational, and practical properties of these indicators, such as monotonicity in species, twinning, monotonicity in distance, strict monotonicity in distance, uniformity of maximizing point sets, computational effort for a set of size~n, single-point contributions, subset selection, and submodularity. We present new theorems -- including a proof of the NP-hardness of the Riesz s-Energy Subset Selection Problem -- and consolidate existing results from the literature. In the second part, we apply these indicators in the NOAH algorithm and analyze search dynamics through an example. We examine how optimizing with one indicator affects the performance of others and propose NOAH adaptations specific to the Max-Min indicator.

The Hypervolume Indicator Hessian Matrix: Analytical Expression, Computational Time Complexity, and Sparsity

The problem of approximating the Pareto front of a multiobjective optimization problem can be reformulated as the problem of finding a set that maximizes the hypervolume indicator. This paper establishes the analytical expression of the Hessian matrix of the mapping from a (fixed size) collection of $n$ points in the $d$-dimensional decision space (or $m$ dimensional objective space) to the scalar hypervolume indicator value. To define the Hessian matrix, the input set is vectorized, and the matrix is derived by analytical differentiation of the mapping from a vectorized set to the hypervolume indicator. The Hessian matrix plays a crucial role in second-order methods, such as the Newton-Raphson optimization method, and it can be used for the verification of local optimal sets. So far, the full analytical expression was only established and analyzed for the relatively simple bi-objective case. This paper will derive the full expression for arbitrary dimensions ($m\geq2$ objective functions). For the practically important three-dimensional case, we also provide an asymptotically efficient algorithm with time complexity in $O(n\log n)$ for the exact computation of the Hessian Matrix' non-zero entries. We establish a sharp bound of $12m-6$ for the number of non-zero entries. Also, for the general $m$-dimensional case, a compact recursive analytical expression is established, and its algorithmic implementation is discussed. Also, for the general case, some sparsity results can be established; these results are implied by the recursive expression. To validate and illustrate the analytically derived algorithms and results, we provide a few numerical examples using Python and Mathematica implementations. Open-source implementations of the algorithms and testing data are made available as a supplement to this paper.

Improving Many-objective Evolutionary Algorithms by Means of Expanded Cone Orders

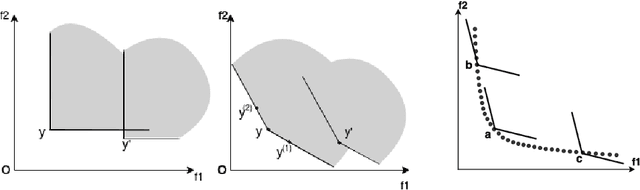
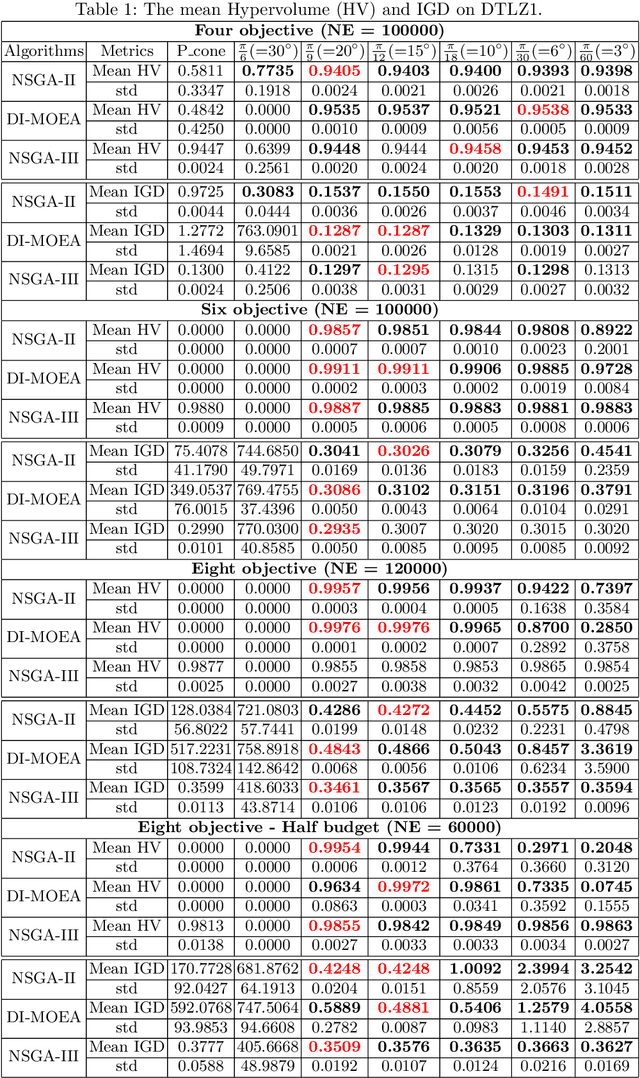
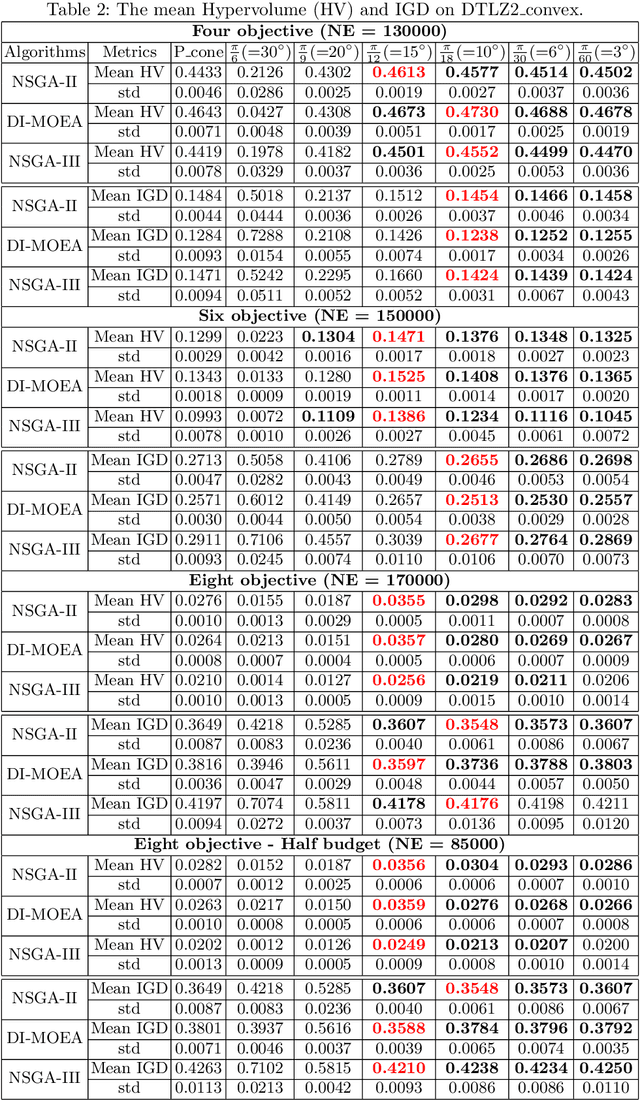
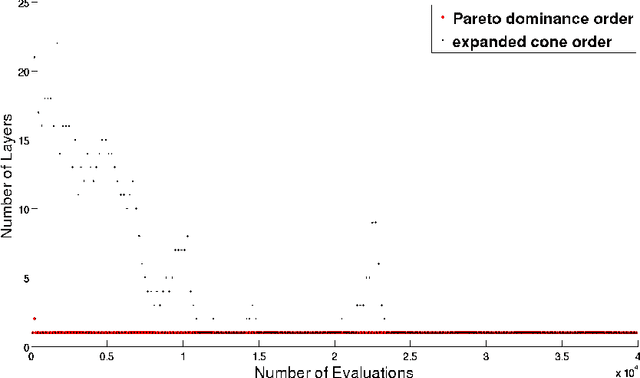
Given a point in m-dimensional objective space, the local environment of a point can be partitioned into the incomparable, the dominated and the dominating region. The ratio between the size of the incomparable region, and the dominated (and dominating) decreases proportionally to $1/2^{m-1}$. Due to this reason, it gets increasingly unlikely that dominating points can be found by random, isotropic mutations. As a remedy to stagnation of search in many objective optimization, in this paper, we suggest to enhance the Pareto dominance order by involving a convex obtuse dominance cone in the convergence phase of an evolutionary optimization algorithm. The approach is integrated in several state-of-the-art multi-objective evolutionary algorithms (MOEAs) and tested on benchmark problems with four, five, six and eight objectives. Computational experiments demonstrate the ability of the expanded cone technique to improve the performance of MOEAs on many-objective optimization problems.

A Tailored NSGA-III Instantiation for Flexible Job Shop Scheduling

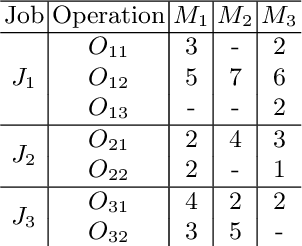
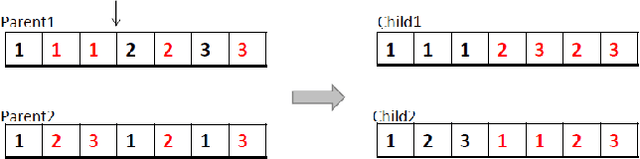
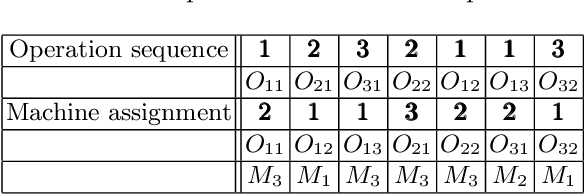
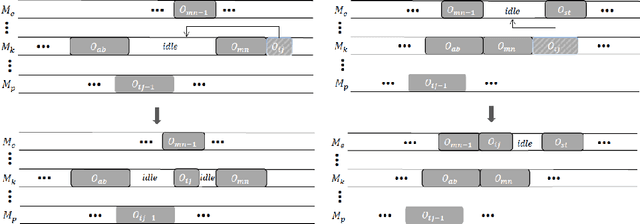
A customized multi-objective evolutionary algorithm (MOEA) is proposed for the multi-objective flexible job shop scheduling problem (FJSP). It uses smart initialization approaches to enrich the first generated population, and proposes various crossover operators to create a better diversity of offspring. Especially, the MIP-EGO configurator, which can tune algorithm parameters, is adopted to automatically tune operator probabilities. Furthermore, different local search strategies are employed to explore the neighborhood for better solutions. In general, the algorithm enhancement strategy can be integrated with any standard EMO algorithm. In this paper, it has been combined with NSGA-III to solve benchmark multi-objective FJSPs, whereas an off-the-shelf implementation of NSGA-III is not capable of solving the FJSP. The experimental results show excellent performance with less computing budget.

Multiobjective Optimization of Classifiers by Means of 3-D Convex Hull Based Evolutionary Algorithm

Finding a good classifier is a multiobjective optimization problem with different error rates and the costs to be minimized. The receiver operating characteristic is widely used in the machine learning community to analyze the performance of parametric classifiers or sets of Pareto optimal classifiers. In order to directly compare two sets of classifiers the area (or volume) under the convex hull can be used as a scalar indicator for the performance of a set of classifiers in receiver operating characteristic space. Recently, the convex hull based multiobjective genetic programming algorithm was proposed and successfully applied to maximize the convex hull area for binary classification problems. The contribution of this paper is to extend this algorithm for dealing with higher dimensional problem formulations. In particular, we discuss problems where parsimony (or classifier complexity) is stated as a third objective and multi-class classification with three different true classification rates to be maximized. The design of the algorithm proposed in this paper is inspired by indicator-based evolutionary algorithms, where first a performance indicator for a solution set is established and then a selection operator is designed that complies with the performance indicator. In this case, the performance indicator will be the volume under the convex hull. The algorithm is tested and analyzed in a proof of concept study on different benchmarks that are designed for measuring its capability to capture relevant parts of a convex hull. Further benchmark and application studies on email classification and feature selection round up the analysis and assess robustness and usefulness of the new algorithm in real world settings.