Comparative Analysis of Indicators for Multiobjective Diversity Optimization
Paper and Code
Oct 24, 2024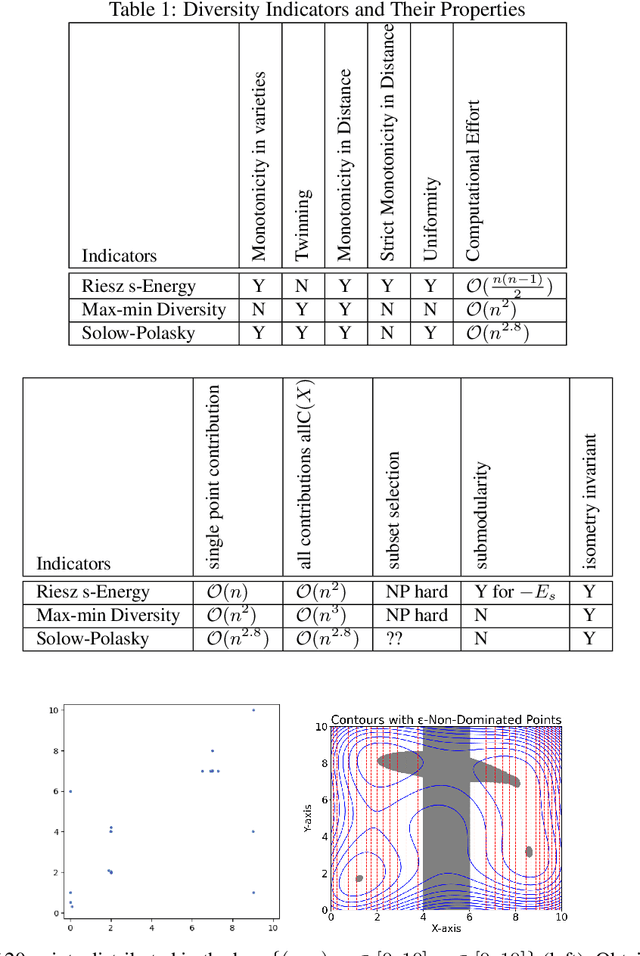

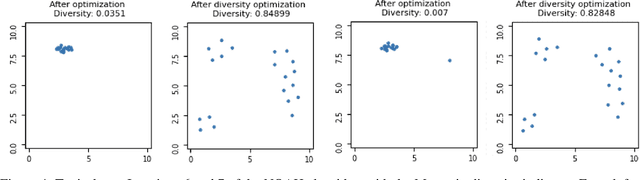
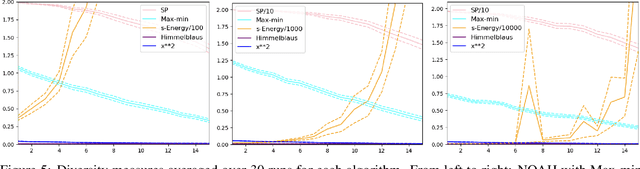
Indicator-based (multiobjective) diversity optimization aims at finding a set of near (Pareto-)optimal solutions that maximizes a diversity indicator, where diversity is typically interpreted as the number of essentially different solutions. Whereas, in the first diversity-oriented evolutionary multiobjective optimization algorithm, the NOAH algorithm by Ulrich and Thiele, the Solow Polasky Diversity (also related to Magnitude) served as a metric, other diversity indicators might be considered, such as the parameter-free Max-Min Diversity, and the Riesz s-Energy, which features uniformly distributed solution sets. In this paper, focusing on multiobjective diversity optimization, we discuss different diversity indicators from the perspective of indicator-based evolutionary algorithms (IBEA) with multiple objectives. We examine theoretical, computational, and practical properties of these indicators, such as monotonicity in species, twinning, monotonicity in distance, strict monotonicity in distance, uniformity of maximizing point sets, computational effort for a set of size~n, single-point contributions, subset selection, and submodularity. We present new theorems -- including a proof of the NP-hardness of the Riesz s-Energy Subset Selection Problem -- and consolidate existing results from the literature. In the second part, we apply these indicators in the NOAH algorithm and analyze search dynamics through an example. We examine how optimizing with one indicator affects the performance of others and propose NOAH adaptations specific to the Max-Min indicator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge