Center-Outward q-Dominance: A Sample-Computable Proxy for Strong Stochastic Dominance in Multi-Objective Optimisation

Stochastic multi-objective optimization (SMOOP) requires ranking multivariate distributions; yet, most empirical studies perform scalarization, which loses information and is unreliable. Based on the optimal transport theory, we introduce the center-outward q-dominance relation and prove it implies strong first-order stochastic dominance (FSD). Also, we develop an empirical test procedure based on q-dominance, and derive an explicit sample size threshold, $n^*(δ)$, to control the Type I error. We verify the usefulness of our approach in two scenarios: (1) as a ranking method in hyperparameter tuning; (2) as a selection method in multi-objective optimization algorithms. For the former, we analyze the final stochastic Pareto sets of seven multi-objective hyperparameter tuners on the YAHPO-MO benchmark tasks with q-dominance, which allows us to compare these tuners when the expected hypervolume indicator (HVI, the most common performance metric) of the Pareto sets becomes indistinguishable. For the latter, we replace the mean value-based selection in the NSGA-II algorithm with $q$-dominance, which shows a superior convergence rate on noise-augmented ZDT benchmark problems. These results establish center-outward q-dominance as a principled, tractable foundation for seeking truly stochastically dominant solutions for SMOOPs.

Benchmarking that Matters: Rethinking Benchmarking for Practical Impact

Benchmarking has driven scientific progress in Evolutionary Computation, yet current practices fall short of real-world needs. Widely used synthetic suites such as BBOB and CEC isolate algorithmic phenomena but poorly reflect the structure, constraints, and information limitations of continuous and mixed-integer optimization problems in practice. This disconnect leads to the misuse of benchmarking suites for competitions, automated algorithm selection, and industrial decision-making, despite these suites being designed for different purposes. We identify key gaps in current benchmarking practices and tooling, including limited availability of real-world-inspired problems, missing high-level features, and challenges in multi-objective and noisy settings. We propose a vision centered on curated real-world-inspired benchmarks, practitioner-accessible feature spaces and community-maintained performance databases. Real progress requires coordinated effort: A living benchmarking ecosystem that evolves with real-world insights and supports both scientific understanding and industrial use.

MECHBench: A Set of Black-Box Optimization Benchmarks originated from Structural Mechanics

Benchmarking is essential for developing and evaluating black-box optimization algorithms, providing a structured means to analyze their search behavior. Its effectiveness relies on carefully selected problem sets used for evaluation. To date, most established benchmark suites for black-box optimization consist of abstract or synthetic problems that only partially capture the complexities of real-world engineering applications, thereby severely limiting the insights that can be gained for application-oriented optimization scenarios and reducing their practical impact. To close this gap, we propose a new benchmarking suite that addresses it by presenting a curated set of optimization benchmarks rooted in structural mechanics. The current implemented benchmarks are derived from vehicle crashworthiness scenarios, which inherently require the use of gradient-free algorithms due to the non-smooth, highly non-linear nature of the underlying models. Within this paper, the reader will find descriptions of the physical context of each case, the corresponding optimization problem formulations, and clear guidelines on how to employ the suite.

Leveraging Lightweight Generators for Memory Efficient Continual Learning

Catastrophic forgetting can be trivially alleviated by keeping all data from previous tasks in memory. Therefore, minimizing the memory footprint while maximizing the amount of relevant information is crucial to the challenge of continual learning. This paper aims to decrease required memory for memory-based continuous learning algorithms. We explore the options of extracting a minimal amount of information, while maximally alleviating forgetting. We propose the usage of lightweight generators based on Singular Value Decomposition to enhance existing continual learning methods, such as A-GEM and Experience Replay. These generators need a minimal amount of memory while being maximally effective. They require no training time, just a single linear-time fitting step, and can capture a distribution effectively from a small number of data samples. Depending on the dataset and network architecture, our results show a significant increase in average accuracy compared to the original methods. Our method shows great potential in minimizing the memory footprint of memory-based continual learning algorithms.

Feasibility-Driven Trust Region Bayesian Optimization

Bayesian optimization is a powerful tool for solving real-world optimization tasks under tight evaluation budgets, making it well-suited for applications involving costly simulations or experiments. However, many of these tasks are also characterized by the presence of expensive constraints whose analytical formulation is unknown and often defined in high-dimensional spaces where feasible regions are small, irregular, and difficult to identify. In such cases, a substantial portion of the optimization budget may be spent just trying to locate the first feasible solution, limiting the effectiveness of existing methods. In this work, we present a Feasibility-Driven Trust Region Bayesian Optimization (FuRBO) algorithm. FuRBO iteratively defines a trust region from which the next candidate solution is selected, using information from both the objective and constraint surrogate models. Our adaptive strategy allows the trust region to shift and resize significantly between iterations, enabling the optimizer to rapidly refocus its search and consistently accelerate the discovery of feasible and good-quality solutions. We empirically demonstrate the effectiveness of FuRBO through extensive testing on the full BBOB-constrained COCO benchmark suite and other physics-inspired benchmarks, comparing it against state-of-the-art baselines for constrained black-box optimization across varying levels of constraint severity and problem dimensionalities ranging from 2 to 60.

LLaMEA-BO: A Large Language Model Evolutionary Algorithm for Automatically Generating Bayesian Optimization Algorithms

Bayesian optimization (BO) is a powerful class of algorithms for optimizing expensive black-box functions, but designing effective BO algorithms remains a manual, expertise-driven task. Recent advancements in Large Language Models (LLMs) have opened new avenues for automating scientific discovery, including the automatic design of optimization algorithms. While prior work has used LLMs within optimization loops or to generate non-BO algorithms, we tackle a new challenge: Using LLMs to automatically generate full BO algorithm code. Our framework uses an evolution strategy to guide an LLM in generating Python code that preserves the key components of BO algorithms: An initial design, a surrogate model, and an acquisition function. The LLM is prompted to produce multiple candidate algorithms, which are evaluated on the established Black-Box Optimization Benchmarking (BBOB) test suite from the COmparing Continuous Optimizers (COCO) platform. Based on their performance, top candidates are selected, combined, and mutated via controlled prompt variations, enabling iterative refinement. Despite no additional fine-tuning, the LLM-generated algorithms outperform state-of-the-art BO baselines in 19 (out of 24) BBOB functions in dimension 5 and generalize well to higher dimensions, and different tasks (from the Bayesmark framework). This work demonstrates that LLMs can serve as algorithmic co-designers, offering a new paradigm for automating BO development and accelerating the discovery of novel algorithmic combinations. The source code is provided at https://github.com/Ewendawi/LLaMEA-BO.

Evolutionary Computation and Large Language Models: A Survey of Methods, Synergies, and Applications

Integrating Large Language Models (LLMs) and Evolutionary Computation (EC) represents a promising avenue for advancing artificial intelligence by combining powerful natural language understanding with optimization and search capabilities. This manuscript explores the synergistic potential of LLMs and EC, reviewing their intersections, complementary strengths, and emerging applications. We identify key opportunities where EC can enhance LLM training, fine-tuning, prompt engineering, and architecture search, while LLMs can, in turn, aid in automating the design, analysis, and interpretation of ECs. The manuscript explores the synergistic integration of EC and LLMs, highlighting their bidirectional contributions to advancing artificial intelligence. It first examines how EC techniques enhance LLMs by optimizing key components such as prompt engineering, hyperparameter tuning, and architecture search, demonstrating how evolutionary methods automate and refine these processes. Secondly, the survey investigates how LLMs improve EC by automating metaheuristic design, tuning evolutionary algorithms, and generating adaptive heuristics, thereby increasing efficiency and scalability. Emerging co-evolutionary frameworks are discussed, showcasing applications across diverse fields while acknowledging challenges like computational costs, interpretability, and algorithmic convergence. The survey concludes by identifying open research questions and advocating for hybrid approaches that combine the strengths of EC and LLMs.

Towards a Deeper Understanding of Reasoning Capabilities in Large Language Models

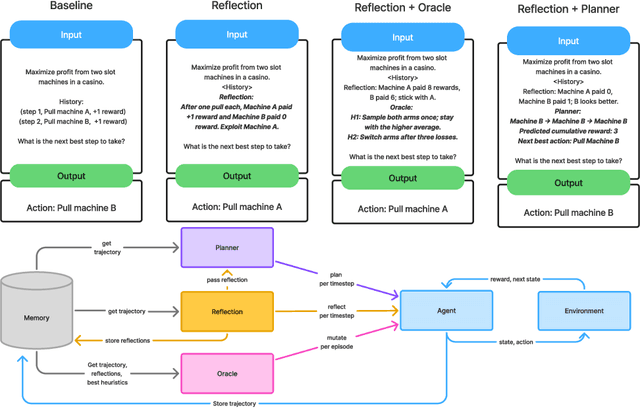
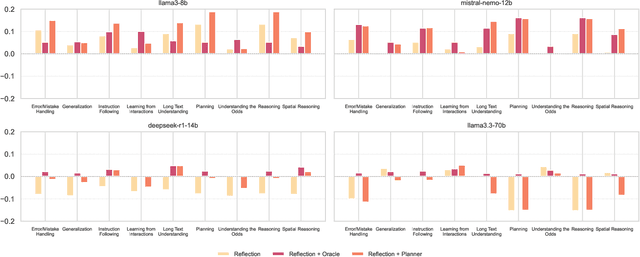
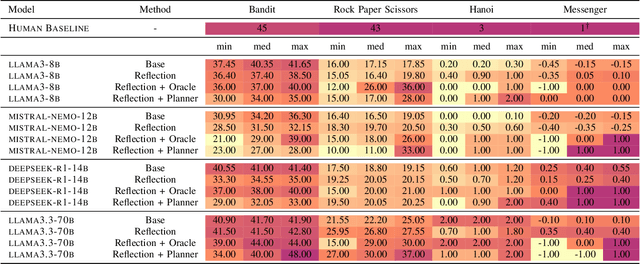
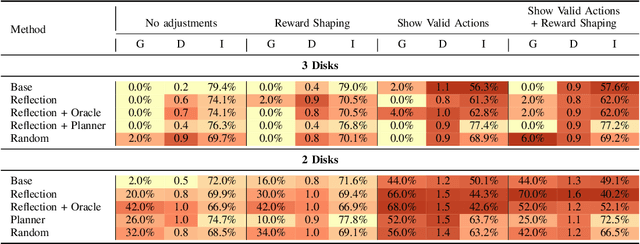
While large language models demonstrate impressive performance on static benchmarks, the true potential of large language models as self-learning and reasoning agents in dynamic environments remains unclear. This study systematically evaluates the efficacy of self-reflection, heuristic mutation, and planning as prompting techniques to test the adaptive capabilities of agents. We conduct experiments with various open-source language models in dynamic environments and find that larger models generally outperform smaller ones, but that strategic prompting can close this performance gap. Second, a too-long prompt can negatively impact smaller models on basic reactive tasks, while larger models show more robust behaviour. Third, advanced prompting techniques primarily benefit smaller models on complex games, but offer less improvement for already high-performing large language models. Yet, we find that advanced reasoning methods yield highly variable outcomes: while capable of significantly improving performance when reasoning and decision-making align, they also introduce instability and can lead to big performance drops. Compared to human performance, our findings reveal little evidence of true emergent reasoning. Instead, large language model performance exhibits persistent limitations in crucial areas such as planning, reasoning, and spatial coordination, suggesting that current-generation large language models still suffer fundamental shortcomings that may not be fully overcome through self-reflective prompting alone. Reasoning is a multi-faceted task, and while reasoning methods like Chain of thought improves multi-step reasoning on math word problems, our findings using dynamic benchmarks highlight important shortcomings in general reasoning capabilities, indicating a need to move beyond static benchmarks to capture the complexity of reasoning.

Why Are You Wrong? Counterfactual Explanations for Language Grounding with 3D Objects

Combining natural language and geometric shapes is an emerging research area with multiple applications in robotics and language-assisted design. A crucial task in this domain is object referent identification, which involves selecting a 3D object given a textual description of the target. Variability in language descriptions and spatial relationships of 3D objects makes this a complex task, increasing the need to better understand the behavior of neural network models in this domain. However, limited research has been conducted in this area. Specifically, when a model makes an incorrect prediction despite being provided with a seemingly correct object description, practitioners are left wondering: "Why is the model wrong?". In this work, we present a method answering this question by generating counterfactual examples. Our method takes a misclassified sample, which includes two objects and a text description, and generates an alternative yet similar formulation that would have resulted in a correct prediction by the model. We have evaluated our approach with data from the ShapeTalk dataset along with three distinct models. Our counterfactual examples maintain the structure of the original description, are semantically similar and meaningful. They reveal weaknesses in the description, model bias and enhance the understanding of the models behavior. Theses insights help practitioners to better interact with systems as well as engineers to improve models.

BLADE: Benchmark suite for LLM-driven Automated Design and Evolution of iterative optimisation heuristics

The application of Large Language Models (LLMs) for Automated Algorithm Discovery (AAD), particularly for optimisation heuristics, is an emerging field of research. This emergence necessitates robust, standardised benchmarking practices to rigorously evaluate the capabilities and limitations of LLM-driven AAD methods and the resulting generated algorithms, especially given the opacity of their design process and known issues with existing benchmarks. To address this need, we introduce BLADE (Benchmark suite for LLM-driven Automated Design and Evolution), a modular and extensible framework specifically designed for benchmarking LLM-driven AAD methods in a continuous black-box optimisation context. BLADE integrates collections of benchmark problems (including MA-BBOB and SBOX-COST among others) with instance generators and textual descriptions aimed at capability-focused testing, such as generalisation, specialisation and information exploitation. It offers flexible experimental setup options, standardised logging for reproducibility and fair comparison, incorporates methods for analysing the AAD process (e.g., Code Evolution Graphs and various visualisation approaches) and facilitates comparison against human-designed baselines through integration with established tools like IOHanalyser and IOHexplainer. BLADE provides an `out-of-the-box' solution to systematically evaluate LLM-driven AAD approaches. The framework is demonstrated through two distinct use cases exploring mutation prompt strategies and function specialisation.