Optimization is Not Enough: Why Problem Formulation Deserves Equal Attention

Black-box optimization is increasingly used in engineering design problems where simulation-based evaluations are costly and gradients are unavailable. In this context, the optimization community has largely analyzed algorithm performance in context-free setups, while not enough attention has been devoted to how problem formulation and domain knowledge may affect the optimization outcomes. We address this gap through a case study in the topology optimization of laminated composite structures, formulated as a black-box optimization problem. Specifically, we consider the design of a cantilever beam under a volume constraint, intending to minimize compliance while optimizing both the structural topology and fiber orientations. To assess the impact of problem formulation, we explicitly separate topology and material design variables and compare two strategies: a concurrent approach that optimizes all variables simultaneously without leveraging physical insight, and a sequential approach that optimizes variables of the same nature in stages. Our results show that context-agnostic strategies consistently lead to suboptimal or non-physical designs. In contrast, the sequential strategy yields better-performing and more interpretable solutions. These findings underscore the value of incorporating, when available, domain knowledge into the optimization process and motivate the development of new black-box benchmarks that reward physically informed and context-aware optimization strategies.

Investigating the Interplay of Parameterization and Optimizer in Gradient-Free Topology Optimization: A Cantilever Beam Case Study

Gradient-free black-box optimization (BBO) is widely used in engineering design and provides a flexible framework for topology optimization (TO), enabling the discovery of high-performing structural designs without requiring gradient information from simulations. Yet, its success depends on two key choices: the geometric parameterization defining the search space and the optimizer exploring it. This study investigates this interplay through a compliance minimization problem for a cantilever beam subject to a connectivity constraint. We benchmark three geometric parameterizations, each combined with three representative BBO algorithms: differential evolution, covariance matrix adaptation evolution strategy, and heteroscedastic evolutionary Bayesian optimization, across 10D, 20D, and 50D design spaces. Results reveal that parameterization quality has a stronger influence on optimization performance than optimizer choice: a well-structured parameterization enables robust and competitive performance across algorithms, whereas weaker representations increase optimizer dependency. Overall, this study highlights the dominant role of geometric parameterization in practical BBO-based TO and shows that algorithm performance and selection cannot be fairly assessed without accounting for the induced design space.

Benchmarking that Matters: Rethinking Benchmarking for Practical Impact

Benchmarking has driven scientific progress in Evolutionary Computation, yet current practices fall short of real-world needs. Widely used synthetic suites such as BBOB and CEC isolate algorithmic phenomena but poorly reflect the structure, constraints, and information limitations of continuous and mixed-integer optimization problems in practice. This disconnect leads to the misuse of benchmarking suites for competitions, automated algorithm selection, and industrial decision-making, despite these suites being designed for different purposes. We identify key gaps in current benchmarking practices and tooling, including limited availability of real-world-inspired problems, missing high-level features, and challenges in multi-objective and noisy settings. We propose a vision centered on curated real-world-inspired benchmarks, practitioner-accessible feature spaces and community-maintained performance databases. Real progress requires coordinated effort: A living benchmarking ecosystem that evolves with real-world insights and supports both scientific understanding and industrial use.

MECHBench: A Set of Black-Box Optimization Benchmarks originated from Structural Mechanics

Benchmarking is essential for developing and evaluating black-box optimization algorithms, providing a structured means to analyze their search behavior. Its effectiveness relies on carefully selected problem sets used for evaluation. To date, most established benchmark suites for black-box optimization consist of abstract or synthetic problems that only partially capture the complexities of real-world engineering applications, thereby severely limiting the insights that can be gained for application-oriented optimization scenarios and reducing their practical impact. To close this gap, we propose a new benchmarking suite that addresses it by presenting a curated set of optimization benchmarks rooted in structural mechanics. The current implemented benchmarks are derived from vehicle crashworthiness scenarios, which inherently require the use of gradient-free algorithms due to the non-smooth, highly non-linear nature of the underlying models. Within this paper, the reader will find descriptions of the physical context of each case, the corresponding optimization problem formulations, and clear guidelines on how to employ the suite.

Feasibility-Driven Trust Region Bayesian Optimization

Bayesian optimization is a powerful tool for solving real-world optimization tasks under tight evaluation budgets, making it well-suited for applications involving costly simulations or experiments. However, many of these tasks are also characterized by the presence of expensive constraints whose analytical formulation is unknown and often defined in high-dimensional spaces where feasible regions are small, irregular, and difficult to identify. In such cases, a substantial portion of the optimization budget may be spent just trying to locate the first feasible solution, limiting the effectiveness of existing methods. In this work, we present a Feasibility-Driven Trust Region Bayesian Optimization (FuRBO) algorithm. FuRBO iteratively defines a trust region from which the next candidate solution is selected, using information from both the objective and constraint surrogate models. Our adaptive strategy allows the trust region to shift and resize significantly between iterations, enabling the optimizer to rapidly refocus its search and consistently accelerate the discovery of feasible and good-quality solutions. We empirically demonstrate the effectiveness of FuRBO through extensive testing on the full BBOB-constrained COCO benchmark suite and other physics-inspired benchmarks, comparing it against state-of-the-art baselines for constrained black-box optimization across varying levels of constraint severity and problem dimensionalities ranging from 2 to 60.

LLaMEA-BO: A Large Language Model Evolutionary Algorithm for Automatically Generating Bayesian Optimization Algorithms

Bayesian optimization (BO) is a powerful class of algorithms for optimizing expensive black-box functions, but designing effective BO algorithms remains a manual, expertise-driven task. Recent advancements in Large Language Models (LLMs) have opened new avenues for automating scientific discovery, including the automatic design of optimization algorithms. While prior work has used LLMs within optimization loops or to generate non-BO algorithms, we tackle a new challenge: Using LLMs to automatically generate full BO algorithm code. Our framework uses an evolution strategy to guide an LLM in generating Python code that preserves the key components of BO algorithms: An initial design, a surrogate model, and an acquisition function. The LLM is prompted to produce multiple candidate algorithms, which are evaluated on the established Black-Box Optimization Benchmarking (BBOB) test suite from the COmparing Continuous Optimizers (COCO) platform. Based on their performance, top candidates are selected, combined, and mutated via controlled prompt variations, enabling iterative refinement. Despite no additional fine-tuning, the LLM-generated algorithms outperform state-of-the-art BO baselines in 19 (out of 24) BBOB functions in dimension 5 and generalize well to higher dimensions, and different tasks (from the Bayesmark framework). This work demonstrates that LLMs can serve as algorithmic co-designers, offering a new paradigm for automating BO development and accelerating the discovery of novel algorithmic combinations. The source code is provided at https://github.com/Ewendawi/LLaMEA-BO.

Why Are You Wrong? Counterfactual Explanations for Language Grounding with 3D Objects

Combining natural language and geometric shapes is an emerging research area with multiple applications in robotics and language-assisted design. A crucial task in this domain is object referent identification, which involves selecting a 3D object given a textual description of the target. Variability in language descriptions and spatial relationships of 3D objects makes this a complex task, increasing the need to better understand the behavior of neural network models in this domain. However, limited research has been conducted in this area. Specifically, when a model makes an incorrect prediction despite being provided with a seemingly correct object description, practitioners are left wondering: "Why is the model wrong?". In this work, we present a method answering this question by generating counterfactual examples. Our method takes a misclassified sample, which includes two objects and a text description, and generates an alternative yet similar formulation that would have resulted in a correct prediction by the model. We have evaluated our approach with data from the ShapeTalk dataset along with three distinct models. Our counterfactual examples maintain the structure of the original description, are semantically similar and meaningful. They reveal weaknesses in the description, model bias and enhance the understanding of the models behavior. Theses insights help practitioners to better interact with systems as well as engineers to improve models.

Cascading CMA-ES Instances for Generating Input-diverse Solution Batches

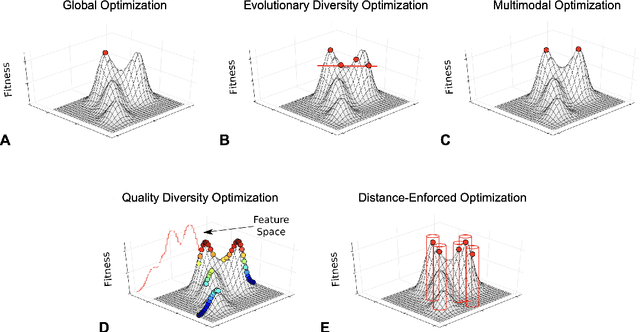
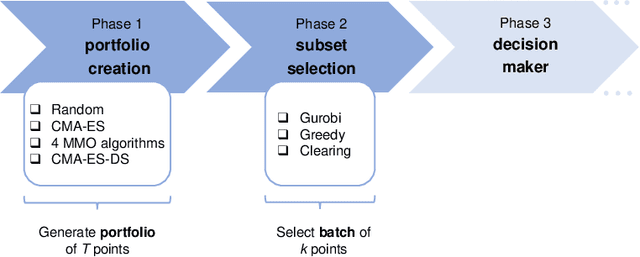
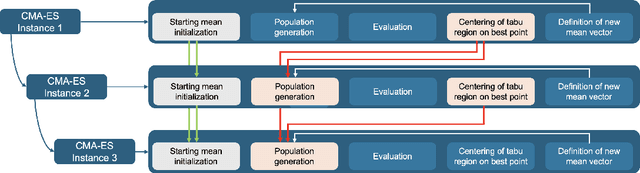
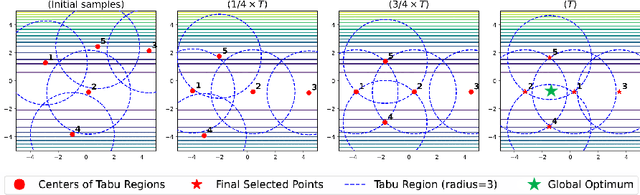
Rather than obtaining a single good solution for a given optimization problem, users often seek alternative design choices, because the best-found solution may perform poorly with respect to additional objectives or constraints that are difficult to capture into the modeling process. Aiming for batches of diverse solutions of high quality is often desirable, as it provides flexibility to accommodate post-hoc user preferences. At the same time, it is crucial that the quality of the best solution found is not compromised. One particular problem setting balancing high quality and diversity is fixing the required minimum distance between solutions while simultaneously obtaining the best possible fitness. Recent work by Santoni et al. [arXiv 2024] revealed that this setting is not well addressed by state-of-the-art algorithms, performing in par or worse than pure random sampling. Driven by this important limitation, we propose a new approach, where parallel runs of the covariance matrix adaptation evolution strategy (CMA-ES) inherit tabu regions in a cascading fashion. We empirically demonstrate that our CMA-ES-Diversity Search (CMA-ES-DS) algorithm generates trajectories that allow to extract high-quality solution batches that respect a given minimum distance requirement, clearly outperforming those obtained from off-the-shelf random sampling, multi-modal optimization algorithms, and standard CMA-ES.

Illuminating the Diversity-Fitness Trade-Off in Black-Box Optimization

In real-world applications, users often favor structurally diverse design choices over one high-quality solution. It is hence important to consider more solutions that decision-makers can compare and further explore based on additional criteria. Alongside the existing approaches of evolutionary diversity optimization, quality diversity, and multimodal optimization, this paper presents a fresh perspective on this challenge by considering the problem of identifying a fixed number of solutions with a pairwise distance above a specified threshold while maximizing their average quality. We obtain first insight into these objectives by performing a subset selection on the search trajectories of different well-established search heuristics, whether specifically designed with diversity in mind or not. We emphasize that the main goal of our work is not to present a new algorithm but to look at the problem in a more fundamental and theoretically tractable way by asking the question: What trade-off exists between the minimum distance within batches of solutions and the average quality of their fitness? These insights also provide us with a way of making general claims concerning the properties of optimization problems that shall be useful in turn for benchmarking algorithms of the approaches enumerated above. A possibly surprising outcome of our empirical study is the observation that naive uniform random sampling establishes a very strong baseline for our problem, hardly ever outperformed by the search trajectories of the considered heuristics. We interpret these results as a motivation to develop algorithms tailored to produce diverse solutions of high average quality.

Automated Federated Learning via Informed Pruning

Federated learning (FL) represents a pivotal shift in machine learning (ML) as it enables collaborative training of local ML models coordinated by a central aggregator, all without the need to exchange local data. However, its application on edge devices is hindered by limited computational capabilities and data communication challenges, compounded by the inherent complexity of Deep Learning (DL) models. Model pruning is identified as a key technique for compressing DL models on devices with limited resources. Nonetheless, conventional pruning techniques typically rely on manually crafted heuristics and demand human expertise to achieve a balance between model size, speed, and accuracy, often resulting in sub-optimal solutions. In this study, we introduce an automated federated learning approach utilizing informed pruning, called AutoFLIP, which dynamically prunes and compresses DL models within both the local clients and the global server. It leverages a federated loss exploration phase to investigate model gradient behavior across diverse datasets and losses, providing insights into parameter significance. Our experiments showcase notable enhancements in scenarios with strong non-IID data, underscoring AutoFLIP's capacity to tackle computational constraints and achieve superior global convergence.