carps: A Framework for Comparing N Hyperparameter Optimizers on M Benchmarks

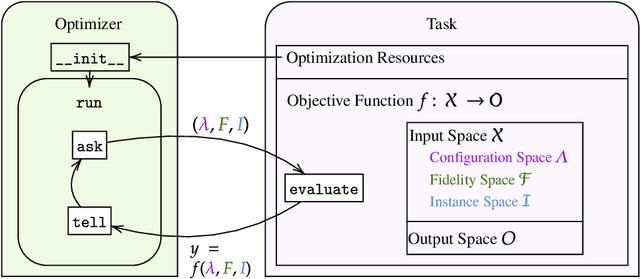
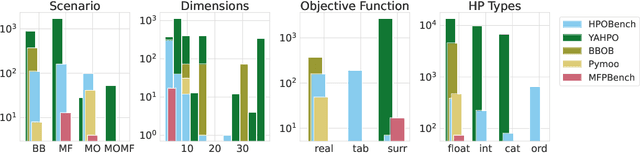
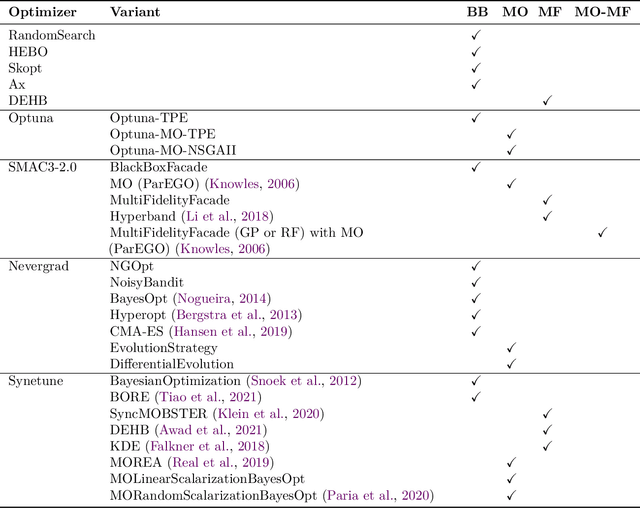
Hyperparameter Optimization (HPO) is crucial to develop well-performing machine learning models. In order to ease prototyping and benchmarking of HPO methods, we propose carps, a benchmark framework for Comprehensive Automated Research Performance Studies allowing to evaluate N optimizers on M benchmark tasks. In this first release of carps, we focus on the four most important types of HPO task types: blackbox, multi-fidelity, multi-objective and multi-fidelity-multi-objective. With 3 336 tasks from 5 community benchmark collections and 28 variants of 9 optimizer families, we offer the biggest go-to library to date to evaluate and compare HPO methods. The carps framework relies on a purpose-built, lightweight interface, gluing together optimizers and benchmark tasks. It also features an analysis pipeline, facilitating the evaluation of optimizers on benchmarks. However, navigating a huge number of tasks while developing and comparing methods can be computationally infeasible. To address this, we obtain a subset of representative tasks by minimizing the star discrepancy of the subset, in the space spanned by the full set. As a result, we propose an initial subset of 10 to 30 diverse tasks for each task type, and include functionality to re-compute subsets as more benchmarks become available, enabling efficient evaluations. We also establish a first set of baseline results on these tasks as a measure for future comparisons. With carps (https://www.github.com/automl/CARP-S), we make an important step in the standardization of HPO evaluation.

Multi-parameter Control for the (1+($λ$,$λ$))-GA on OneMax via Deep Reinforcement Learning

It is well known that evolutionary algorithms can benefit from dynamic choices of the key parameters that control their behavior, to adjust their search strategy to the different stages of the optimization process. A prominent example where dynamic parameter choices have shown a provable super-constant speed-up is the $(1+(\lambda,\lambda))$ Genetic Algorithm optimizing the OneMax function. While optimal parameter control policies result in linear expected running times, this is not possible with static parameter choices. This result has spurred a lot of interest in parameter control policies. However, many works, in particular theoretical running time analyses, focus on controlling one single parameter. Deriving policies for controlling multiple parameters remains very challenging. In this work we reconsider the problem of the $(1+(\lambda,\lambda))$ Genetic Algorithm optimizing OneMax. We decouple its four main parameters and investigate how well state-of-the-art deep reinforcement learning techniques can approximate good control policies. We show that although making deep reinforcement learning learn effectively is a challenging task, once it works, it is very powerful and is able to find policies that outperform all previously known control policies on the same benchmark. Based on the results found through reinforcement learning, we derive a simple control policy that consistently outperforms the default theory-recommended setting by $27\%$ and the irace-tuned policy, the strongest existing control policy on this benchmark, by $13\%$, for all tested problem sizes up to $40{,}000$.

On the Importance of Reward Design in Reinforcement Learning-based Dynamic Algorithm Configuration: A Case Study on OneMax with (1+($λ$,$λ$))-GA

Dynamic Algorithm Configuration (DAC) has garnered significant attention in recent years, particularly in the prevalence of machine learning and deep learning algorithms. Numerous studies have leveraged the robustness of decision-making in Reinforcement Learning (RL) to address the optimization challenges associated with algorithm configuration. However, making an RL agent work properly is a non-trivial task, especially in reward design, which necessitates a substantial amount of handcrafted knowledge based on domain expertise. In this work, we study the importance of reward design in the context of DAC via a case study on controlling the population size of the $(1+(\lambda,\lambda))$-GA optimizing OneMax. We observed that a poorly designed reward can hinder the RL agent's ability to learn an optimal policy because of a lack of exploration, leading to both scalability and learning divergence issues. To address those challenges, we propose the application of a reward shaping mechanism to facilitate enhanced exploration of the environment by the RL agent. Our work not only demonstrates the ability of RL in dynamically configuring the $(1+(\lambda,\lambda))$-GA, but also confirms the advantages of reward shaping in the scalability of RL agents across various sizes of OneMax problems.

Cascading CMA-ES Instances for Generating Input-diverse Solution Batches

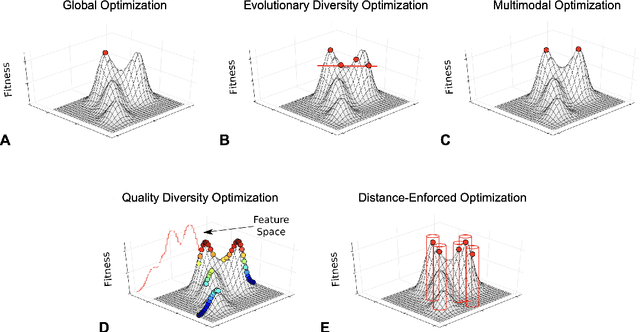
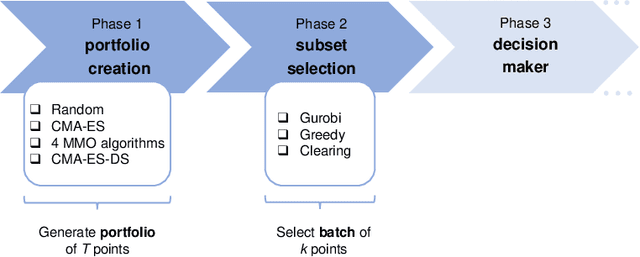
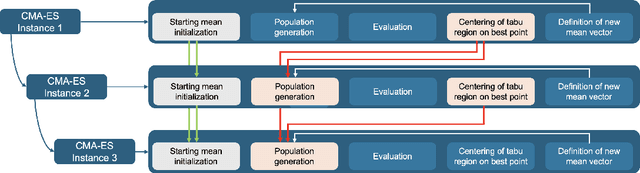
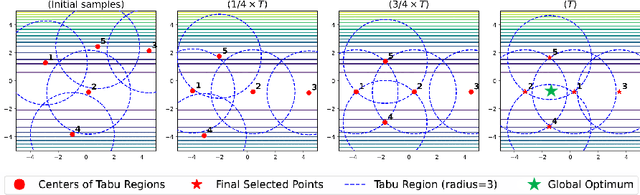
Rather than obtaining a single good solution for a given optimization problem, users often seek alternative design choices, because the best-found solution may perform poorly with respect to additional objectives or constraints that are difficult to capture into the modeling process. Aiming for batches of diverse solutions of high quality is often desirable, as it provides flexibility to accommodate post-hoc user preferences. At the same time, it is crucial that the quality of the best solution found is not compromised. One particular problem setting balancing high quality and diversity is fixing the required minimum distance between solutions while simultaneously obtaining the best possible fitness. Recent work by Santoni et al. [arXiv 2024] revealed that this setting is not well addressed by state-of-the-art algorithms, performing in par or worse than pure random sampling. Driven by this important limitation, we propose a new approach, where parallel runs of the covariance matrix adaptation evolution strategy (CMA-ES) inherit tabu regions in a cascading fashion. We empirically demonstrate that our CMA-ES-Diversity Search (CMA-ES-DS) algorithm generates trajectories that allow to extract high-quality solution batches that respect a given minimum distance requirement, clearly outperforming those obtained from off-the-shelf random sampling, multi-modal optimization algorithms, and standard CMA-ES.

MO-IOHinspector: Anytime Benchmarking of Multi-Objective Algorithms using IOHprofiler

Benchmarking is one of the key ways in which we can gain insight into the strengths and weaknesses of optimization algorithms. In sampling-based optimization, considering the anytime behavior of an algorithm can provide valuable insights for further developments. In the context of multi-objective optimization, this anytime perspective is not as widely adopted as in the single-objective context. In this paper, we propose a new software tool which uses principles from unbounded archiving as a logging structure. This leads to a clearer separation between experimental design and subsequent analysis decisions. We integrate this approach as a new Python module into the IOHprofiler framework and demonstrate the benefits of this approach by showcasing the ability to change indicators, aggregations, and ranking procedures during the analysis pipeline.

Illuminating the Diversity-Fitness Trade-Off in Black-Box Optimization

In real-world applications, users often favor structurally diverse design choices over one high-quality solution. It is hence important to consider more solutions that decision-makers can compare and further explore based on additional criteria. Alongside the existing approaches of evolutionary diversity optimization, quality diversity, and multimodal optimization, this paper presents a fresh perspective on this challenge by considering the problem of identifying a fixed number of solutions with a pairwise distance above a specified threshold while maximizing their average quality. We obtain first insight into these objectives by performing a subset selection on the search trajectories of different well-established search heuristics, whether specifically designed with diversity in mind or not. We emphasize that the main goal of our work is not to present a new algorithm but to look at the problem in a more fundamental and theoretically tractable way by asking the question: What trade-off exists between the minimum distance within batches of solutions and the average quality of their fitness? These insights also provide us with a way of making general claims concerning the properties of optimization problems that shall be useful in turn for benchmarking algorithms of the approaches enumerated above. A possibly surprising outcome of our empirical study is the observation that naive uniform random sampling establishes a very strong baseline for our problem, hardly ever outperformed by the search trajectories of the considered heuristics. We interpret these results as a motivation to develop algorithms tailored to produce diverse solutions of high average quality.

Hybridizing Target- and SHAP-encoded Features for Algorithm Selection in Mixed-variable Black-box Optimization

Exploratory landscape analysis (ELA) is a well-established tool to characterize optimization problems via numerical features. ELA is used for problem comprehension, algorithm design, and applications such as automated algorithm selection and configuration. Until recently, however, ELA was limited to search spaces with either continuous or discrete variables, neglecting problems with mixed variable types. This gap was addressed in a recent study that uses an approach based on target-encoding to compute exploratory landscape features for mixedvariable problems. In this work, we investigate an alternative encoding scheme based on SHAP values. While these features do not lead to better results in the algorithm selection setting considered in previous work, the two different encoding mechanisms exhibit complementary performance. Combining both feature sets into a hybrid approach outperforms each encoding mechanism individually. Finally, we experiment with two different ways of meta-selecting between the two feature sets. Both approaches are capable of taking advantage of the performance complementarity of the models trained on target-encoded and SHAP-encoded feature sets, respectively.

A Survey of Meta-features Used for Automated Selection of Algorithms for Black-box Single-objective Continuous Optimization

The selection of the most appropriate algorithm to solve a given problem instance, known as algorithm selection, is driven by the potential to capitalize on the complementary performance of different algorithms across sets of problem instances. However, determining the optimal algorithm for an unseen problem instance has been shown to be a challenging task, which has garnered significant attention from researchers in recent years. In this survey, we conduct an overview of the key contributions to algorithm selection in the field of single-objective continuous black-box optimization. We present ongoing work in representation learning of meta-features for optimization problem instances, algorithm instances, and their interactions. We also study machine learning models for automated algorithm selection, configuration, and performance prediction. Through this analysis, we identify gaps in the state of the art, based on which we present ideas for further development of meta-feature representations.

Generalization Ability of Feature-based Performance Prediction Models: A Statistical Analysis across Benchmarks

This study examines the generalization ability of algorithm performance prediction models across various benchmark suites. Comparing the statistical similarity between the problem collections with the accuracy of performance prediction models that are based on exploratory landscape analysis features, we observe that there is a positive correlation between these two measures. Specifically, when the high-dimensional feature value distributions between training and testing suites lack statistical significance, the model tends to generalize well, in the sense that the testing errors are in the same range as the training errors. Two experiments validate these findings: one involving the standard benchmark suites, the BBOB and CEC collections, and another using five collections of affine combinations of BBOB problem instances.

Quantifying Individual and Joint Module Impact in Modular Optimization Frameworks

This study explores the influence of modules on the performance of modular optimization frameworks for continuous single-objective black-box optimization. There is an extensive variety of modules to choose from when designing algorithm variants, however, there is a rather limited understanding of how each module individually influences the algorithm performance and how the modules interact with each other when combined. We use the functional ANOVA (f-ANOVA) framework to quantify the influence of individual modules and module combinations for two algorithms, the modular Covariance Matrix Adaptation (modCMA) and the modular Differential Evolution (modDE). We analyze the performance data from 324 modCMA and 576 modDE variants on the BBOB benchmark collection, for two problem dimensions, and three computational budgets. Noteworthy findings include the identification of important modules that strongly influence the performance of modCMA, such as the~\textit{weights\ option} and~\textit{mirrored} modules for low dimensional problems, and the~\textit{base\ sampler} for high dimensional problems. The large individual influence of the~\textit{lpsr} module makes it very important for the performance of modDE, regardless of the problem dimensionality and the computational budget. When comparing modCMA and modDE, modDE undergoes a shift from individual modules being more influential, to module combinations being more influential, while modCMA follows the opposite pattern, with an increase in problem dimensionality and computational budget.