On the Importance of Reward Design in Reinforcement Learning-based Dynamic Algorithm Configuration: A Case Study on OneMax with (1+($λ$,$λ$))-GA

Dynamic Algorithm Configuration (DAC) has garnered significant attention in recent years, particularly in the prevalence of machine learning and deep learning algorithms. Numerous studies have leveraged the robustness of decision-making in Reinforcement Learning (RL) to address the optimization challenges associated with algorithm configuration. However, making an RL agent work properly is a non-trivial task, especially in reward design, which necessitates a substantial amount of handcrafted knowledge based on domain expertise. In this work, we study the importance of reward design in the context of DAC via a case study on controlling the population size of the $(1+(\lambda,\lambda))$-GA optimizing OneMax. We observed that a poorly designed reward can hinder the RL agent's ability to learn an optimal policy because of a lack of exploration, leading to both scalability and learning divergence issues. To address those challenges, we propose the application of a reward shaping mechanism to facilitate enhanced exploration of the environment by the RL agent. Our work not only demonstrates the ability of RL in dynamically configuring the $(1+(\lambda,\lambda))$-GA, but also confirms the advantages of reward shaping in the scalability of RL agents across various sizes of OneMax problems.

Athanor: Local Search over Abstract Constraint Specifications

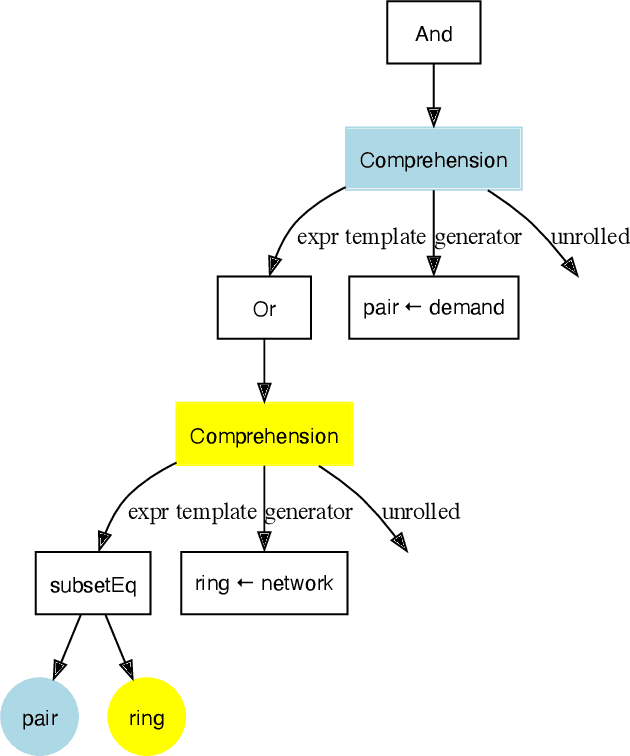
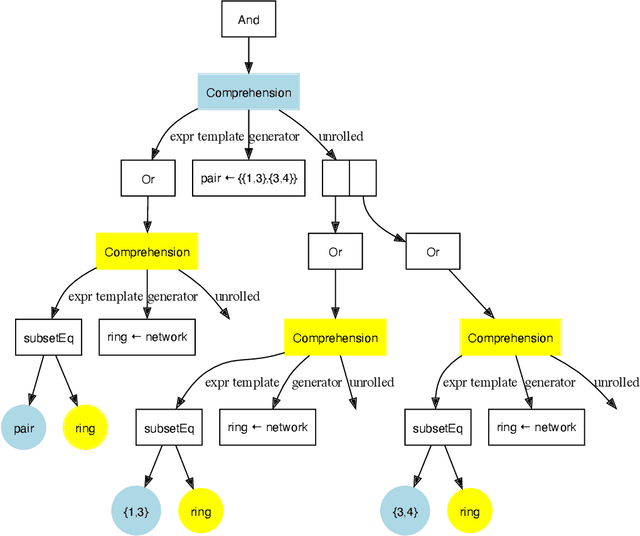
Local search is a common method for solving combinatorial optimisation problems. We focus on general-purpose local search solvers that accept as input a constraint model - a declarative description of a problem consisting of a set of decision variables under a set of constraints. Existing approaches typically take as input models written in solver-independent constraint modelling languages like MiniZinc. The Athanor solver we describe herein differs in that it begins from a specification of a problem in the abstract constraint specification language Essence, which allows problems to be described without commitment to low-level modelling decisions through its support for a rich set of abstract types. The advantage of proceeding from Essence is that the structure apparent in a concise, abstract specification of a problem can be exploited to generate high quality neighbourhoods automatically, avoiding the difficult task of identifying that structure in an equivalent constraint model. Based on the twin benefits of neighbourhoods derived from high level types and the scalability derived by searching directly over those types, our empirical results demonstrate strong performance in practice relative to existing solution methods.

Frugal Algorithm Selection

When solving decision and optimisation problems, many competing algorithms (model and solver choices) have complementary strengths. Typically, there is no single algorithm that works well for all instances of a problem. Automated algorithm selection has been shown to work very well for choosing a suitable algorithm for a given instance. However, the cost of training can be prohibitively large due to running candidate algorithms on a representative set of training instances. In this work, we explore reducing this cost by choosing a subset of the training instances on which to train. We approach this problem in three ways: using active learning to decide based on prediction uncertainty, augmenting the algorithm predictors with a timeout predictor, and collecting training data using a progressively increasing timeout. We evaluate combinations of these approaches on six datasets from ASLib and present the reduction in labelling cost achieved by each option.

Using Automated Algorithm Configuration for Parameter Control

Dynamic Algorithm Configuration (DAC) tackles the question of how to automatically learn policies to control parameters of algorithms in a data-driven fashion. This question has received considerable attention from the evolutionary community in recent years. Having a good benchmark collection to gain structural understanding on the effectiveness and limitations of different solution methods for DAC is therefore strongly desirable. Following recent work on proposing DAC benchmarks with well-understood theoretical properties and ground truth information, in this work, we suggest as a new DAC benchmark the controlling of the key parameter $\lambda$ in the $(1+(\lambda,\lambda))$~Genetic Algorithm for solving OneMax problems. We conduct a study on how to solve the DAC problem via the use of (static) automated algorithm configuration on the benchmark, and propose techniques to significantly improve the performance of the approach. Our approach is able to consistently outperform the default parameter control policy of the benchmark derived from previous theoretical work on sufficiently large problem sizes. We also present new findings on the landscape of the parameter-control search policies and propose methods to compute stronger baselines for the benchmark via numerical approximations of the true optimal policies.

A portfolio-based analysis method for competition results

Competitions such as the MiniZinc Challenges or the SAT competitions have been very useful sources for comparing performance of different solving approaches and for advancing the state-of-the-arts of the fields. Traditional competition setting often focuses on producing a ranking between solvers based on their average performance across a wide range of benchmark problems and instances. While this is a sensible way to assess the relative performance of solvers, such ranking does not necessarily reflect the full potential of a solver, especially when we want to utilise a portfolio of solvers instead of a single one for solving a new problem. In this paper, I will describe a portfolio-based analysis method which can give complementary insights into the performance of participating solvers in a competition. The method is demonstrated on the results of the MiniZinc Challenges and new insights gained from the portfolio viewpoint are presented.

A Framework for Generating Informative Benchmark Instances

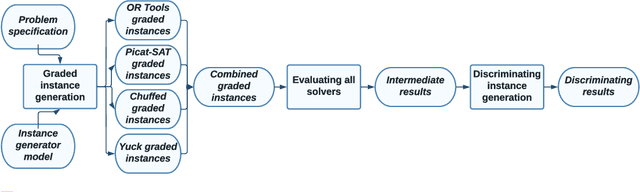
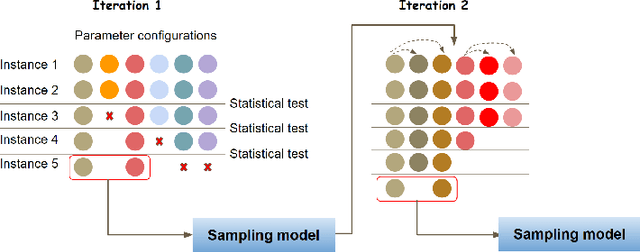
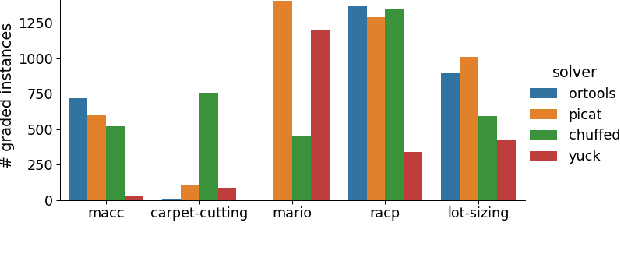
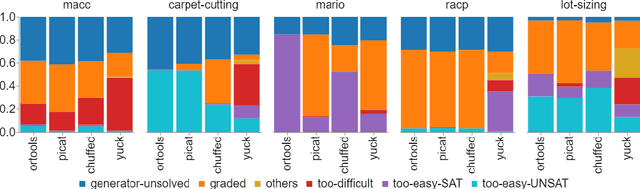
Benchmarking is an important tool for assessing the relative performance of alternative solving approaches. However, the utility of benchmarking is limited by the quantity and quality of the available problem instances. Modern constraint programming languages typically allow the specification of a class-level model that is parameterised over instance data. This separation presents an opportunity for automated approaches to generate instance data that define instances that are graded (solvable at a certain difficulty level for a solver) or can discriminate between two solving approaches. In this paper, we introduce a framework that combines these two properties to generate a large number of benchmark instances, purposely generated for effective and informative benchmarking. We use five problems that were used in the MiniZinc competition to demonstrate the usage of our framework. In addition to producing a ranking among solvers, our framework gives a broader understanding of the behaviour of each solver for the whole instance space; for example by finding subsets of instances where the solver performance significantly varies from its average performance.

Theory-inspired Parameter Control Benchmarks for Dynamic Algorithm Configuration

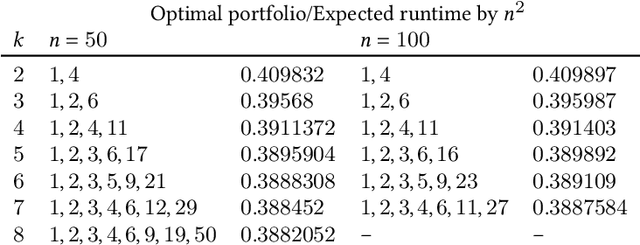
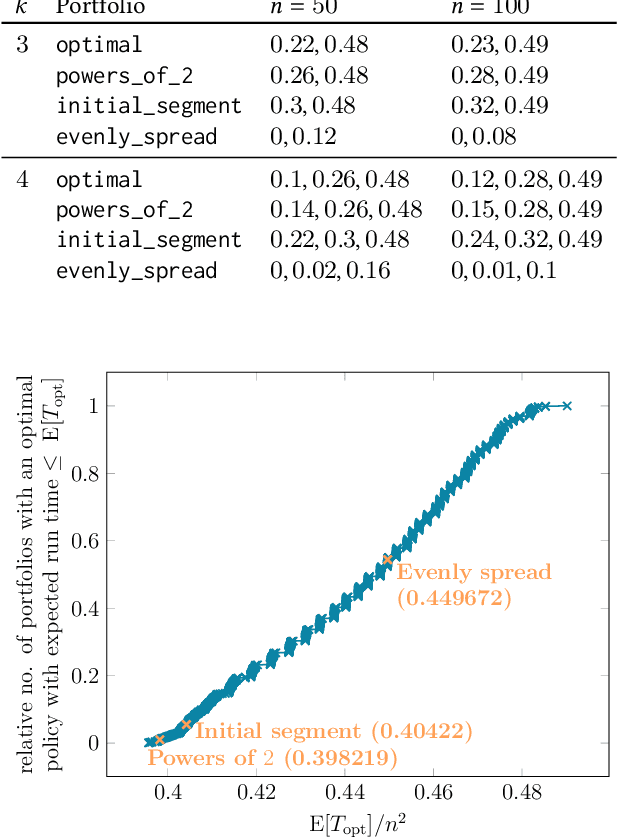
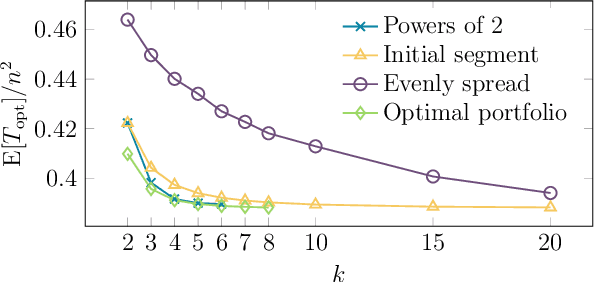
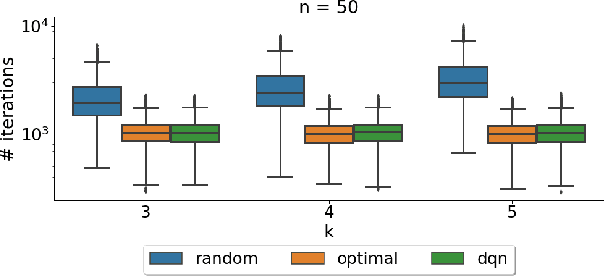
It has long been observed that the performance of evolutionary algorithms and other randomized search heuristics can benefit from a non-static choice of the parameters that steer their optimization behavior. Mechanisms that identify suitable configurations on the fly ("parameter control") or via a dedicated training process ("dynamic algorithm configuration") are therefore an important component of modern evolutionary computation frameworks. Several approaches to address the dynamic parameter setting problem exist, but we barely understand which ones to prefer for which applications. As in classical benchmarking, problem collections with a known ground truth can offer very meaningful insights in this context. Unfortunately, settings with well-understood control policies are very rare. One of the few exceptions for which we know which parameter settings minimize the expected runtime is the LeadingOnes problem. We extend this benchmark by analyzing optimal control policies that can select the parameters only from a given portfolio of possible values. This also allows us to compute optimal parameter portfolios of a given size. We demonstrate the usefulness of our benchmarks by analyzing the behavior of the DDQN reinforcement learning approach for dynamic algorithm configuration.

Efficient Incremental Modelling and Solving

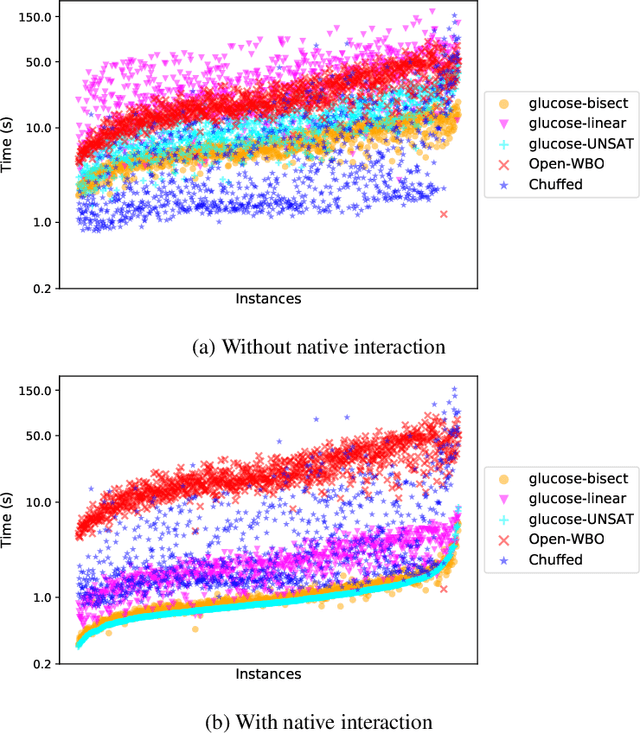
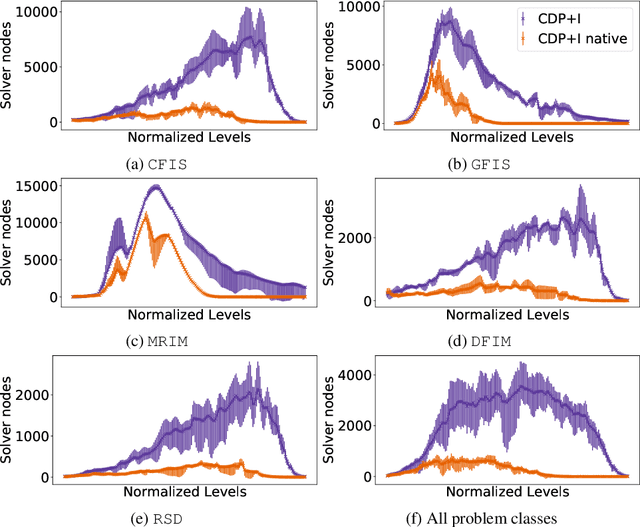
In various scenarios, a single phase of modelling and solving is either not sufficient or not feasible to solve the problem at hand. A standard approach to solving AI planning problems, for example, is to incrementally extend the planning horizon and solve the problem of trying to find a plan of a particular length. Indeed, any optimization problem can be solved as a sequence of decision problems in which the objective value is incrementally updated. Another example is constraint dominance programming (CDP), in which search is organized into a sequence of levels. The contribution of this work is to enable a native interaction between SAT solvers and the automated modelling system Savile Row to support efficient incremental modelling and solving. This allows adding new decision variables, posting new constraints and removing existing constraints (via assumptions) between incremental steps. Two additional benefits of the native coupling of modelling and solving are the ability to retain learned information between SAT solver calls and to enable SAT assumptions, further improving flexibility and efficiency. Experiments on one optimisation problem and five pattern mining tasks demonstrate that the native interaction between the modelling system and SAT solver consistently improves performance significantly.

Exploring Instance Generation for Automated Planning

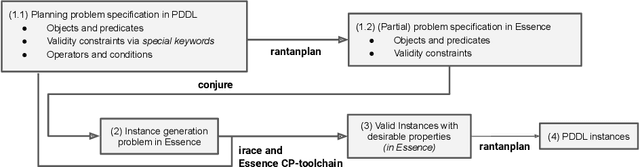
Many of the core disciplines of artificial intelligence have sets of standard benchmark problems well known and widely used by the community when developing new algorithms. Constraint programming and automated planning are examples of these areas, where the behaviour of a new algorithm is measured by how it performs on these instances. Typically the efficiency of each solving method varies not only between problems, but also between instances of the same problem. Therefore, having a diverse set of instances is crucial to be able to effectively evaluate a new solving method. Current methods for automatic generation of instances for Constraint Programming problems start with a declarative model and search for instances with some desired attributes, such as hardness or size. We first explore the difficulties of adapting this approach to generate instances starting from problem specifications written in PDDL, the de-facto standard language of the automated planning community. We then propose a new approach where the whole planning problem description is modelled using Essence, an abstract modelling language that allows expressing high-level structures without committing to a particular low level representation in PDDL.

Towards Portfolios of Streamlined Constraint Models: A Case Study with the Balanced Academic Curriculum Problem

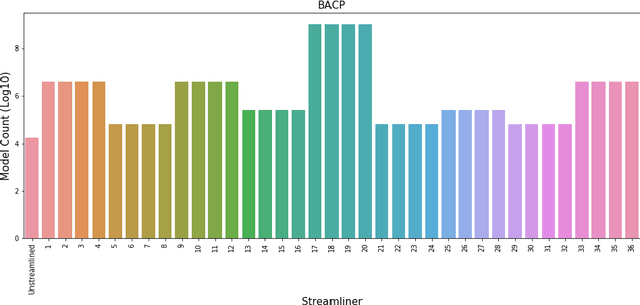
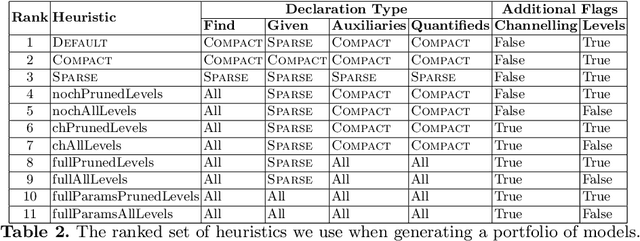
Augmenting a base constraint model with additional constraints can strengthen the inferences made by a solver and therefore reduce search effort. We focus on the automatic addition of streamliner constraints, derived from the types present in an abstract Essence specification of a problem class of interest, which trade completeness for potentially very significant reduction in search. The refinement of streamlined Essence specifications into constraint models suitable for input to constraint solvers gives rise to a large number of modelling choices in addition to those required for the base Essence specification. Previous automated streamlining approaches have been limited in evaluating only a single default model for each streamlined specification. In this paper we explore the effect of model selection in the context of streamlined specifications. We propose a new best-first search method that generates a portfolio of Pareto Optimal streamliner-model combinations by evaluating for each streamliner a portfolio of models to search and explore the variability in performance and find the optimal model. Various forms of racing are utilised to constrain the computational cost of training.