Improving Time and Memory Efficiency of Genetic Algorithms by Storing Populations as Minimum Spanning Trees of Patches

In many applications of evolutionary algorithms the computational cost of applying operators and storing populations is comparable to the cost of fitness evaluation. Furthermore, by knowing what exactly has changed in an individual by an operator, it is possible to recompute fitness value much more efficiently than from scratch. The associated time and memory improvements have been available for simple evolutionary algorithms, few specific genetic algorithms and in the context of gray-box optimization, but not for all algorithms, and the main reason is that it is difficult to achieve in algorithms using large arbitrarily structured populations. This paper makes a first step towards improving this situation. We show that storing the population as a minimum spanning tree, where vertices correspond to individuals but only contain meta-information about them, and edges store structural differences, or patches, between the individuals, is a viable alternative to the straightforward implementation. Our experiments suggest that significant, even asymptotic, improvements -- including execution of crossover operators! -- can be achieved in terms of both memory usage and computational costs.

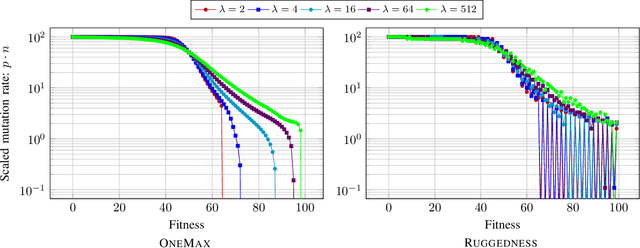
Using Automated Algorithm Configuration for Parameter Control

Dynamic Algorithm Configuration (DAC) tackles the question of how to automatically learn policies to control parameters of algorithms in a data-driven fashion. This question has received considerable attention from the evolutionary community in recent years. Having a good benchmark collection to gain structural understanding on the effectiveness and limitations of different solution methods for DAC is therefore strongly desirable. Following recent work on proposing DAC benchmarks with well-understood theoretical properties and ground truth information, in this work, we suggest as a new DAC benchmark the controlling of the key parameter $\lambda$ in the $(1+(\lambda,\lambda))$~Genetic Algorithm for solving OneMax problems. We conduct a study on how to solve the DAC problem via the use of (static) automated algorithm configuration on the benchmark, and propose techniques to significantly improve the performance of the approach. Our approach is able to consistently outperform the default parameter control policy of the benchmark derived from previous theoretical work on sufficiently large problem sizes. We also present new findings on the landscape of the parameter-control search policies and propose methods to compute stronger baselines for the benchmark via numerical approximations of the true optimal policies.

Lazy Parameter Tuning and Control: Choosing All Parameters Randomly From a Power-Law Distribution

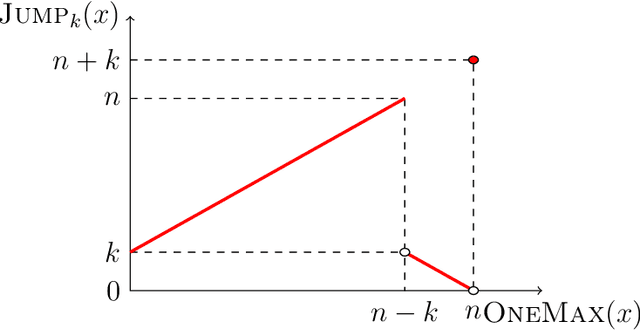
Most evolutionary algorithms have multiple parameters and their values drastically affect the performance. Due to the often complicated interplay of the parameters, setting these values right for a particular problem (parameter tuning) is a challenging task . This task becomes even more complicated when the optimal parameter values change significantly during the run of the algorithm since then a dynamic parameter choice (parameter control) is necessary. In this work, we propose a lazy but effective solution, namely choosing all parameter values (where this makes sense) in each iteration randomly from a suitably scaled power-law distribution. To demonstrate the effectiveness of this approach, we perform runtime analyses of the $(1+(\lambda,\lambda))$ genetic algorithm with all three parameters chosen in this manner. We show this algorithm on the one hand can imitate simple hill-climbers like the $(1+1)$ EA, giving the same asymptotic runtime on problems like OneMax, LeadingOnes, or Minimum Spanning Tree. On the other hand, this algorithm is also very efficient on jump functions, where the best static parameters are very different from those necessary to optimize simple problems. We prove a performance guarantee that is comparable, sometimes even better, than the best performance known for static parameters. We complement our theoretical results with a rigorous empirical study confirming what the asymptotic runtime results suggest.

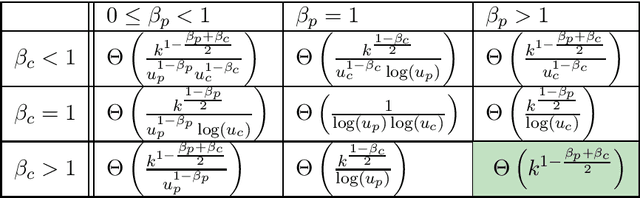
Blending Dynamic Programming with Monte Carlo Simulation for Bounding the Running Time of Evolutionary Algorithms

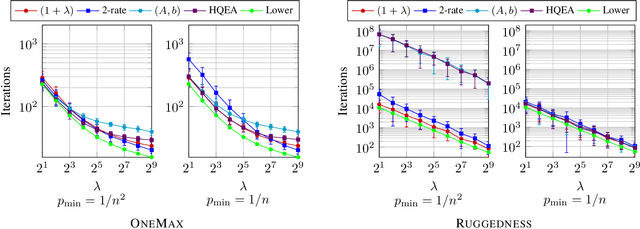
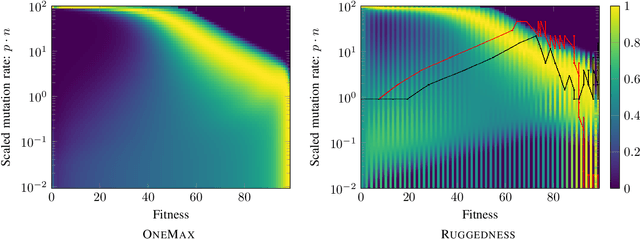
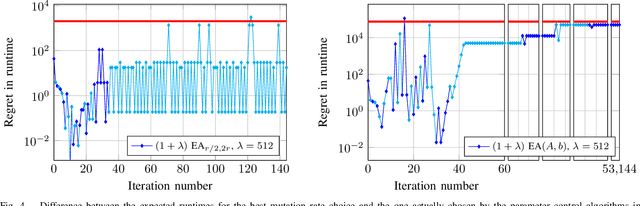
With the goal to provide absolute lower bounds for the best possible running times that can be achieved by $(1+\lambda)$-type search heuristics on common benchmark problems, we recently suggested a dynamic programming approach that computes optimal expected running times and the regret values inferred when deviating from the optimal parameter choice. Our previous work is restricted to problems for which transition probabilities between different states can be expressed by relatively simple mathematical expressions. With the goal to cover broader sets of problems, we suggest in this work an extension of the dynamic programming approach to settings in which the transition probabilities cannot necessarily be computed exactly, but in which they can be approximated numerically, up to arbitrary precision, by Monte Carlo sampling. We apply our hybrid Monte Carlo dynamic programming approach to a concatenated jump function and demonstrate how the obtained bounds can be used to gain a deeper understanding into parameter control schemes.

Optimal Static Mutation Strength Distributions for the $(1+λ)$ Evolutionary Algorithm on OneMax

Most evolutionary algorithms have parameters, which allow a great flexibility in controlling their behavior and adapting them to new problems. To achieve the best performance, it is often needed to control some of the parameters during optimization, which gave rise to various parameter control methods. In recent works, however, similar advantages have been shown, and even proven, for sampling parameter values from certain, often heavy-tailed, fixed distributions. This produced a family of algorithms currently known as "fast evolution strategies" and "fast genetic algorithms". However, only little is known so far about the influence of these distributions on the performance of evolutionary algorithms, and about the relationships between (dynamic) parameter control and (static) parameter sampling. We contribute to the body of knowledge by presenting, for the first time, an algorithm that computes the optimal static distributions, which describe the mutation operator used in the well-known simple $(1+\lambda)$ evolutionary algorithm on a classic benchmark problem OneMax. We show that, for large enough population sizes, such optimal distributions may be surprisingly complicated and counter-intuitive. We investigate certain properties of these distributions, and also evaluate the performance regrets of the $(1+\lambda)$ evolutionary algorithm using commonly used mutation distributions.

First Steps Towards a Runtime Analysis When Starting With a Good Solution

The mathematical runtime analysis of evolutionary algorithms traditionally regards the time an algorithm needs to find a solution of a certain quality when initialized with a random population. In practical applications it may be possible to guess solutions that are better than random ones. We start a mathematical runtime analysis for such situations. We observe that different algorithms profit to a very different degree from a better initialization. We also show that the optimal parameterization of the algorithm can depend strongly on the quality of the initial solutions. To overcome this difficulty, self-adjusting and randomized heavy-tailed parameter choices can be profitable. Finally, we observe a larger gap between the performance of the best evolutionary algorithm we found and the corresponding black-box complexity. This could suggest that evolutionary algorithms better exploiting good initial solutions are still to be found. These first findings stem from analyzing the performance of the $(1+1)$ evolutionary algorithm and the static, self-adjusting, and heavy-tailed $(1 + (\lambda,\lambda))$ GA on the OneMax benchmark, but we are optimistic that the question how to profit from good initial solutions is interesting beyond these first examples.

Optimal Mutation Rates for the $$ EA on OneMax

The OneMax problem, alternatively known as the Hamming distance problem, is often referred to as the "drosophila of evolutionary computation (EC)", because of its high relevance in theoretical and empirical analyses of EC approaches. It is therefore surprising that even for the simplest of all mutation-based algorithms, Randomized Local Search and the (1+1) EA, the optimal mutation rates were determined only very recently, in a GECCO 2019 poster. In this work, we extend the analysis of optimal mutation rates to two variants of the $(1+\lambda)$ EA and to the $(1+\lambda)$ RLS. To do this, we use dynamic programming and, for the $(1+\lambda)$ EA, numeric optimization, both requiring $\Theta(n^3)$ time for problem dimension $n$. With this in hand, we compute for all population sizes $\lambda \in \{2^i \mid 0 \le i \le 18\}$ and for problem dimension $n \in \{1000, 2000, 5000\}$ which mutation rates minimize the expected running time and which ones maximize the expected progress. Our results do not only provide a lower bound against which we can measure common evolutionary approaches, but we also obtain insight into the structure of these optimal parameter choices. For example, we show that, for large population sizes, the best number of bits to flip is not monotone in the distance to the optimum. We also observe that the expected remaining running time are not necessarily unimodal for the $(1+\lambda)$ EA$_{0 \rightarrow 1}$ with shifted mutation.

The $(1+(λ,λ))$ Genetic Algorithm for Permutations

The $(1+(\lambda,\lambda))$ genetic algorithm is a bright example of an evolutionary algorithm which was developed based on the insights from theoretical findings. This algorithm uses crossover, and it was shown to asymptotically outperform all mutation-based evolutionary algorithms even on simple problems like OneMax. Subsequently it was studied on a number of other problems, but all of these were pseudo-Boolean. We aim at improving this situation by proposing an adaptation of the $(1+(\lambda,\lambda))$ genetic algorithm to permutation-based problems. Such an adaptation is required, because permutations are noticeably different from bit strings in some key aspects, such as the number of possible mutations and their mutual dependence. We also present the first runtime analysis of this algorithm on a permutation-based problem called Ham whose properties resemble those of OneMax. On this problem, where the simple mutation-based algorithms have the running time of $\Theta(n^2 \log n)$ for problem size $n$, the $(1+(\lambda,\lambda))$ genetic algorithm finds the optimum in $O(n^2)$ fitness queries. We augment this analysis with experiments, which show that this algorithm is also fast in practice.

Fixed-Target Runtime Analysis

Runtime analysis aims at contributing to our understanding of evolutionary algorithms through mathematical analyses of their runtimes. In the context of discrete optimization problems, runtime analysis classically studies the time needed to find an optimal solution. However, both from a practical and a theoretical viewpoint, more fine-grained performance measures are needed. Two complementary approaches have been suggested: fixed-budget analysis and fixed-target analysis. In this work, we conduct an in-depth study on the advantages and limitations of fixed-target analyses. We show that, different from fixed-budget analyses, many classical methods from the runtime analysis of discrete evolutionary algorithms yield fixed-target results without greater effort. We use this to conduct a number of new fixed-target analyses. However, we also point out examples where an extension of the existing runtime result to a fixed-target result is highly non-trivial.

Fast Mutation in Crossover-based Algorithms

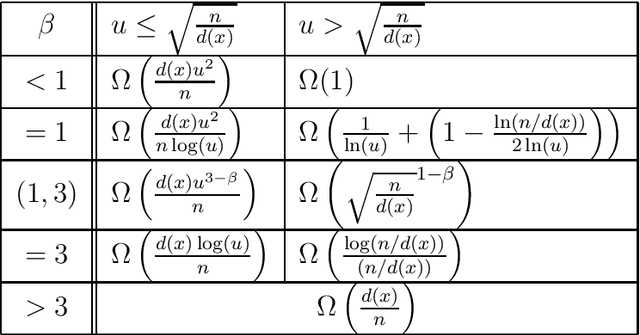
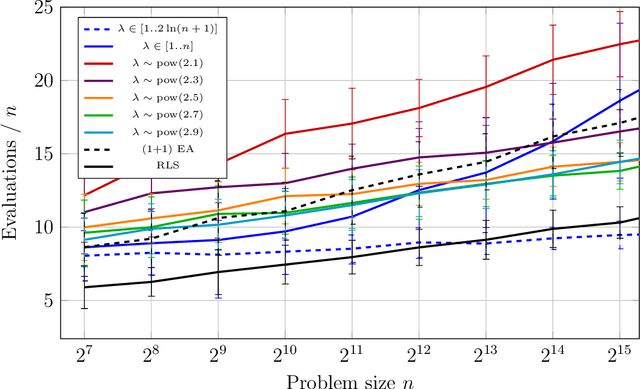
The heavy-tailed mutation operator proposed in Doerr et al. (GECCO 2017), called fast mutation to agree with the previously used language, so far was successfully used only in purely mutation-based algorithms. There, it can relieve the algorithm designer from finding the optimal mutation rate and nevertheless obtain a performance close to the one that the optimal mutation rate gives. In this first runtime analysis of a crossover-based algorithm using a heavy-tailed choice of the mutation rate, we show an even stronger impact. With a heavy-tailed mutation rate, the runtime of the $(1+(\lambda,\lambda))$ genetic algorithm on the OneMax benchmark function becomes linear in the problem size. This is asymptotically faster than with any static mutation rate and is the same asymptotic runtime that can be obtained with a self-adjusting choice of the mutation rate. This result is complemented by an empirical study which shows the effectiveness of the fast mutation also on random MAX-3SAT instances.