Fast Re-Optimization of LeadingOnes with Frequent Changes

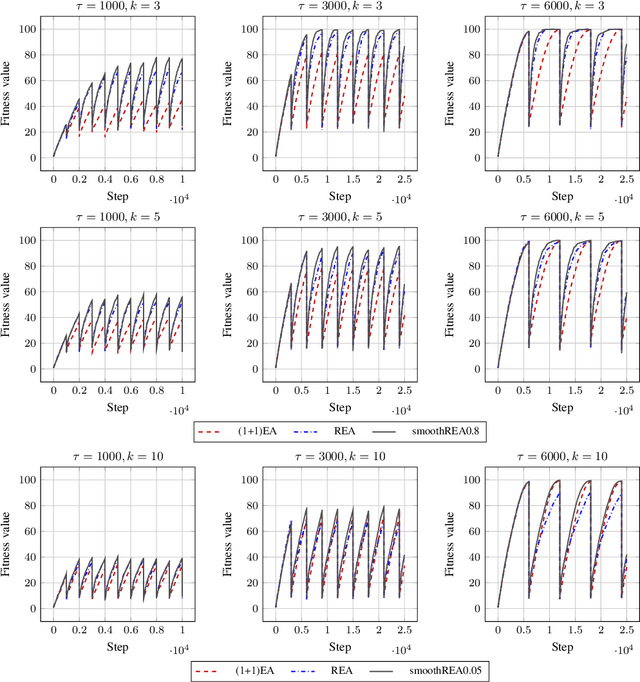
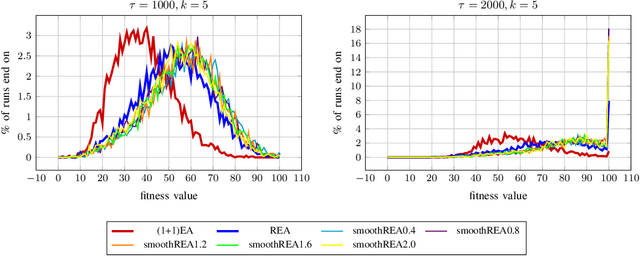
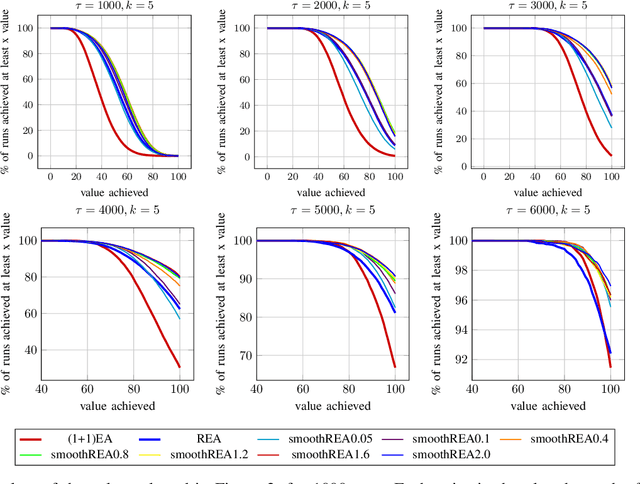
In real-world optimization scenarios, the problem instance that we are asked to solve may change during the optimization process, e.g., when new information becomes available or when the environmental conditions change. In such situations, one could hope to achieve reasonable performance by continuing the search from the best solution found for the original problem. Likewise, one may hope that when solving several problem instances that are similar to each other, it can be beneficial to ``warm-start'' the optimization process of the second instance by the best solution found for the first. However, it was shown in [Doerr et al., GECCO 2019] that even when initialized with structurally good solutions, evolutionary algorithms can have a tendency to replace these good solutions by structurally worse ones, resulting in optimization times that have no advantage over the same algorithms started from scratch. Doerr et al. also proposed a diversity mechanism to overcome this problem. Their approach balances greedy search around a best-so-far solution for the current problem with search in the neighborhood around the best-found solution for the previous instance. In this work, we first show that the re-optimization approach suggested by Doerr et al. reaches a limit when the problem instances are prone to more frequent changes. More precisely, we show that they get stuck on the dynamic LeadingOnes problem in which the target string changes periodically. We then propose a modification of their algorithm which interpolates between greedy search around the previous-best and the current-best solution. We empirically evaluate our smoothed re-optimization algorithm on LeadingOnes instances with various frequencies of change and with different perturbation factors and show that it outperforms both a fully restarted (1+1) Evolutionary Algorithm and the re-optimization approach by Doerr et al.

Blending Dynamic Programming with Monte Carlo Simulation for Bounding the Running Time of Evolutionary Algorithms

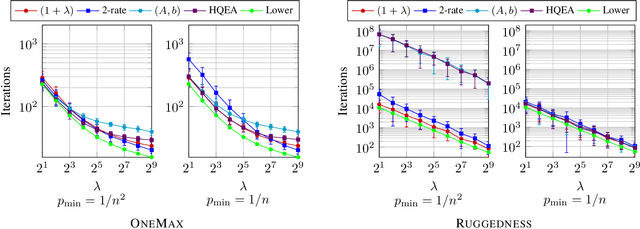
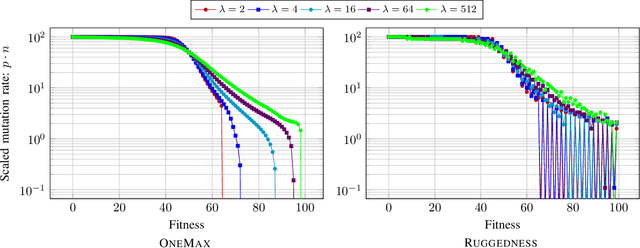
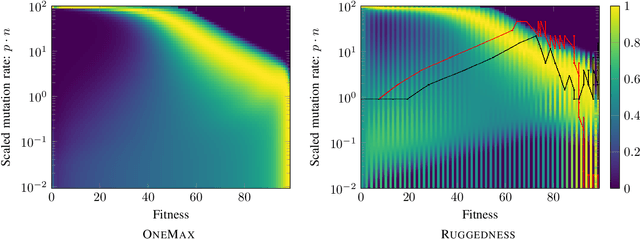
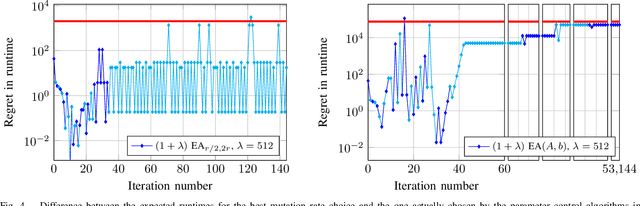
With the goal to provide absolute lower bounds for the best possible running times that can be achieved by $(1+\lambda)$-type search heuristics on common benchmark problems, we recently suggested a dynamic programming approach that computes optimal expected running times and the regret values inferred when deviating from the optimal parameter choice. Our previous work is restricted to problems for which transition probabilities between different states can be expressed by relatively simple mathematical expressions. With the goal to cover broader sets of problems, we suggest in this work an extension of the dynamic programming approach to settings in which the transition probabilities cannot necessarily be computed exactly, but in which they can be approximated numerically, up to arbitrary precision, by Monte Carlo sampling. We apply our hybrid Monte Carlo dynamic programming approach to a concatenated jump function and demonstrate how the obtained bounds can be used to gain a deeper understanding into parameter control schemes.

Hybridizing the 1/5-th Success Rule with Q-Learning for Controlling the Mutation Rate of an Evolutionary Algorithm

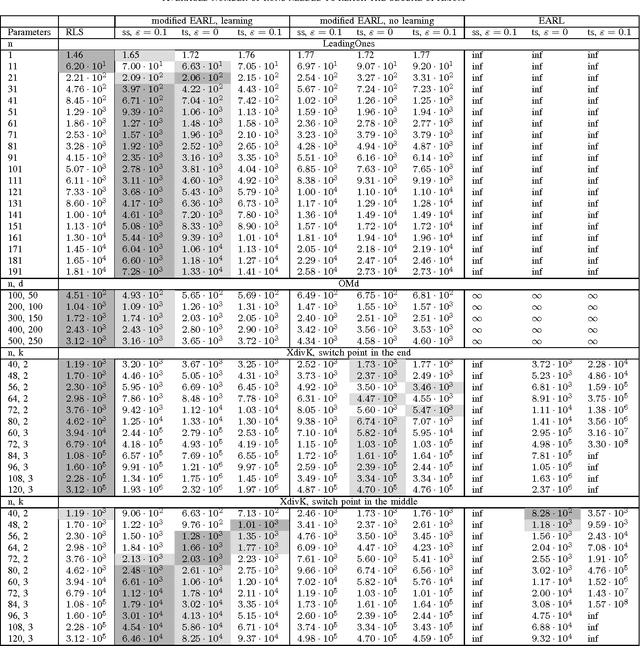
It is well known that evolutionary algorithms (EAs) achieve peak performance only when their parameters are suitably tuned to the given problem. Even more, it is known that the best parameter values can change during the optimization process. Parameter control mechanisms are techniques developed to identify and to track these values. Recently, a series of rigorous theoretical works confirmed the superiority of several parameter control techniques over EAs with best possible static parameters. Among these results are examples for controlling the mutation rate of the $(1+\lambda)$~EA when optimizing the OneMax problem. However, it was shown in [Rodionova et al., GECCO'19] that the quality of these techniques strongly depends on the offspring population size $\lambda$. We introduce in this work a new hybrid parameter control technique, which combines the well-known one-fifth success rule with Q-learning. We demonstrate that our HQL mechanism achieves equal or superior performance to all techniques tested in [Rodionova et al., GECCO'19] and this -- in contrast to previous parameter control methods -- simultaneously for all offspring population sizes $\lambda$. We also show that the promising performance of HQL is not restricted to OneMax, but extends to several other benchmark problems.

Offspring Population Size Matters when Comparing Evolutionary Algorithms with Self-Adjusting Mutation Rates

We analyze the performance of the 2-rate $(1+\lambda)$ Evolutionary Algorithm (EA) with self-adjusting mutation rate control, its 3-rate counterpart, and a $(1+\lambda)$~EA variant using multiplicative update rules on the OneMax problem. We compare their efficiency for offspring population sizes ranging up to $\lambda=3,200$ and problem sizes up to $n=100,000$. Our empirical results show that the ranking of the algorithms is very consistent across all tested dimensions, but strongly depends on the population size. While for small values of $\lambda$ the 2-rate EA performs best, the multiplicative updates become superior for starting for some threshold value of $\lambda$ between 50 and 100. Interestingly, for population sizes around 50, the $(1+\lambda)$~EA with static mutation rates performs on par with the best of the self-adjusting algorithms. We also consider how the lower bound $p_{\min}$ for the mutation rate influences the efficiency of the algorithms. We observe that for the 2-rate EA and the EA with multiplicative update rules the more generous bound $p_{\min}=1/n^2$ gives better results than $p_{\min}=1/n$ when $\lambda$ is small. For both algorithms the situation reverses for large~$\lambda$.

Reinforcement Learning Based Dynamic Selection of Auxiliary Objectives with Preserving of the Best Found Solution

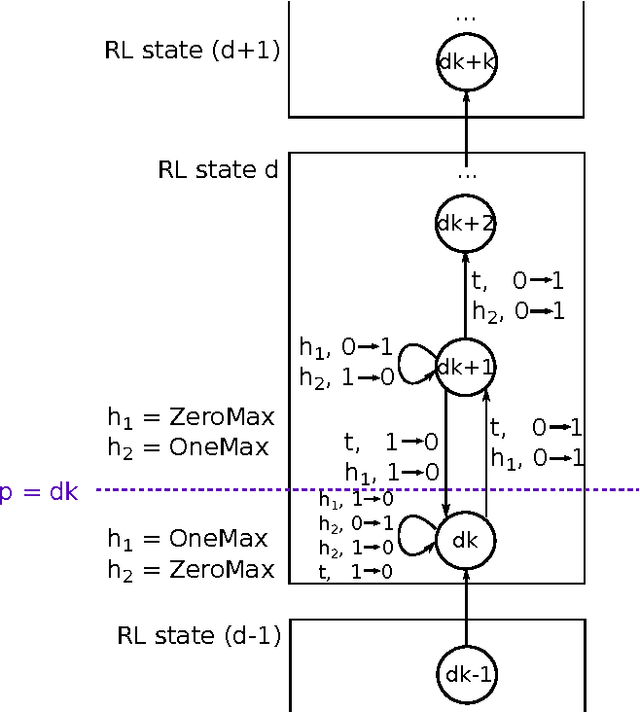
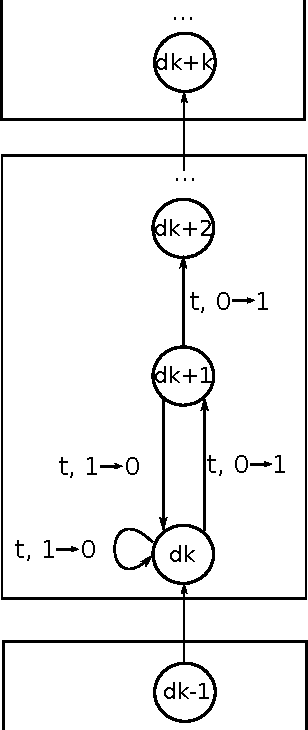
Efficiency of single-objective optimization can be improved by introducing some auxiliary objectives. Ideally, auxiliary objectives should be helpful. However, in practice, objectives may be efficient on some optimization stages but obstructive on others. In this paper we propose a modification of the EA+RL method which dynamically selects optimized objectives using reinforcement learning. The proposed modification prevents from losing the best found solution. We analysed the proposed modification and compared it with the EA+RL method and Random Local Search on XdivK, Generalized OneMax and LeadingOnes problems. The proposed modification outperforms the EA+RL method on all problem instances. It also outperforms the single objective approach on the most problem instances. We also provide detailed analysis of how different components of the considered algorithms influence efficiency of optimization. In addition, we present theoretical analysis of the proposed modification on the XdivK problem.

Adaptive Parameter Selection in Evolutionary Algorithms by Reinforcement Learning with Dynamic Discretization of Parameter Range

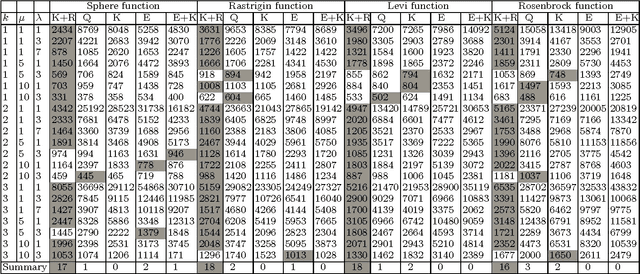
Online parameter controllers for evolutionary algorithms adjust values of parameters during the run of an evolutionary algorithm. Recently a new efficient parameter controller based on reinforcement learning was proposed by Karafotias et al. In this method ranges of parameters are discretized into several intervals before the run. However, performing adaptive discretization during the run may increase efficiency of an evolutionary algorithm. Aleti et al. proposed another efficient controller with adaptive discretization. In the present paper we propose a parameter controller based on reinforcement learning with adaptive discretization. The proposed controller is compared with the existing parameter adjusting methods on several test problems using different configurations of an evolutionary algorithm. For the test problems, we consider four continuous functions, namely the sphere function, the Rosenbrock function, the Levi function and the Rastrigin function. Results show that the new controller outperforms the other controllers on most of the considered test problems.