Fast Re-Optimization of LeadingOnes with Frequent Changes

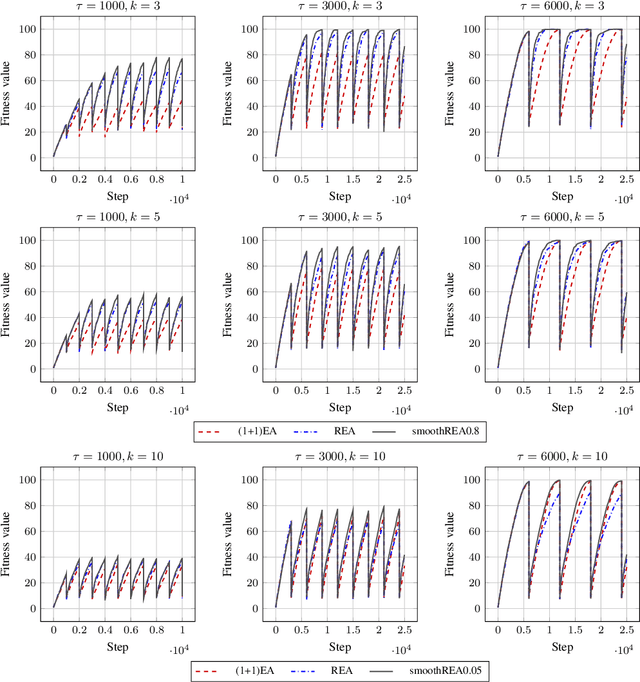
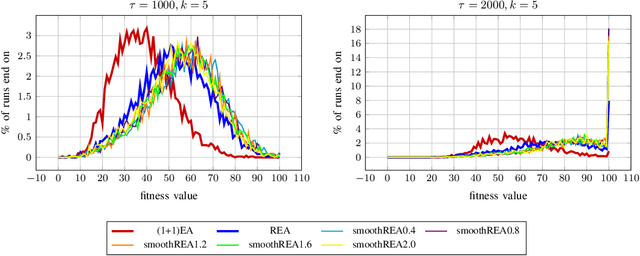
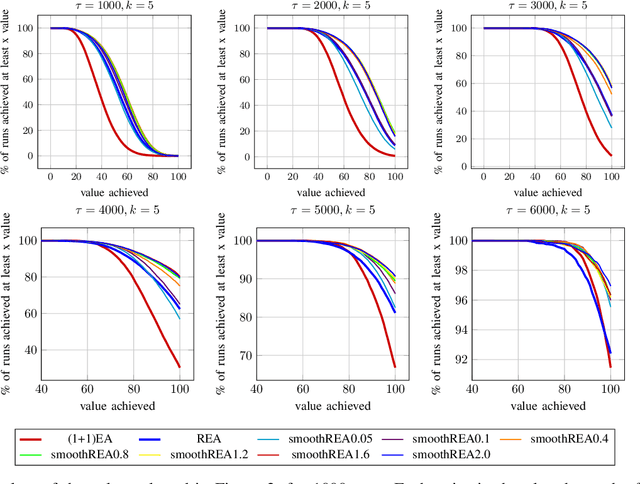
In real-world optimization scenarios, the problem instance that we are asked to solve may change during the optimization process, e.g., when new information becomes available or when the environmental conditions change. In such situations, one could hope to achieve reasonable performance by continuing the search from the best solution found for the original problem. Likewise, one may hope that when solving several problem instances that are similar to each other, it can be beneficial to ``warm-start'' the optimization process of the second instance by the best solution found for the first. However, it was shown in [Doerr et al., GECCO 2019] that even when initialized with structurally good solutions, evolutionary algorithms can have a tendency to replace these good solutions by structurally worse ones, resulting in optimization times that have no advantage over the same algorithms started from scratch. Doerr et al. also proposed a diversity mechanism to overcome this problem. Their approach balances greedy search around a best-so-far solution for the current problem with search in the neighborhood around the best-found solution for the previous instance. In this work, we first show that the re-optimization approach suggested by Doerr et al. reaches a limit when the problem instances are prone to more frequent changes. More precisely, we show that they get stuck on the dynamic LeadingOnes problem in which the target string changes periodically. We then propose a modification of their algorithm which interpolates between greedy search around the previous-best and the current-best solution. We empirically evaluate our smoothed re-optimization algorithm on LeadingOnes instances with various frequencies of change and with different perturbation factors and show that it outperforms both a fully restarted (1+1) Evolutionary Algorithm and the re-optimization approach by Doerr et al.

Black-Box Complexity of the Binary Value Function

The binary value function, or BinVal, has appeared in several studies in theory of evolutionary computation as one of the extreme examples of linear pseudo-Boolean functions. Its unbiased black-box complexity was previously shown to be at most $\lceil \log_2 n \rceil + 2$, where $n$ is the problem size. We augment it with an upper bound of $\log_2 n + 2.42141558 - o(1)$, which is more precise for many values of $n$. We also present a lower bound of $\log_2 n + 1.1186406 - o(1)$. Additionally, we prove that BinVal is an easiest function among all unimodal pseudo-Boolean functions at least for unbiased algorithms.

Better Fixed-Arity Unbiased Black-Box Algorithms

In their GECCO'12 paper, Doerr and Doerr proved that the $k$-ary unbiased black-box complexity of OneMax on $n$ bits is $O(n/k)$ for $2\le k\le O(\log n)$. We propose an alternative strategy for achieving this unbiased black-box complexity when $3\le k\le\log_2 n$. While it is based on the same idea of block-wise optimization, it uses $k$-ary unbiased operators in a different way. For each block of size $2^{k-1}-1$ we set up, in $O(k)$ queries, a virtual coordinate system, which enables us to use an arbitrary unrestricted algorithm to optimize this block. This is possible because this coordinate system introduces a bijection between unrestricted queries and a subset of $k$-ary unbiased operators. We note that this technique does not depend on OneMax being solved and can be used in more general contexts. This together constitutes an algorithm which is conceptually simpler than the one by Doerr and Doerr, and at the same time achieves better constant factors in the asymptotic notation. Our algorithm works in $(2+o(1))\cdot n/(k-1)$, where $o(1)$ relates to $k$. Our experimental evaluation of this algorithm shows its efficiency already for $3\le k\le6$.