Lens-descriptor guided evolutionary algorithm for optimization of complex optical systems with glass choice

Designing high-performance optical lenses entails exploring a high-dimensional, tightly constrained space of surface curvatures, glass choices, element thicknesses, and spacings. In practice, standard optimizers (e.g., gradient-based local search and evolutionary strategies) often converge to a single local optimum, overlooking many comparably good alternatives that matter for downstream engineering decisions. We propose the Lens Descriptor-Guided Evolutionary Algorithm (LDG-EA), a two-stage framework for multimodal lens optimization. LDG-EA first partitions the design space into behavior descriptors defined by curvature-sign patterns and material indices, then learns a probabilistic model over descriptors to allocate evaluations toward promising regions. Within each descriptor, LDG-EA applies the Hill-Valley Evolutionary Algorithm with covariance-matrix self-adaptation to recover multiple distinct local minima, optionally followed by gradient-based refinement. On a 24-variable (18 continuous and 6 integer), six-element Double-Gauss topology, LDG-EA generates on average around 14500 candidate minima spanning 636 unique descriptors, an order of magnitude more than a CMA-ES baseline, while keeping wall-clock time at one hour scale. Although the best LDG-EA design is slightly worse than a fine-tuned reference lens, it remains in the same performance range. Overall, the proposed LDG-EA produces a diverse set of solutions while maintaining competitive quality within practical computational budgets and wall-clock time.

Selection of Filters for Photonic Crystal Spectrometer Using Domain-Aware Evolutionary Algorithms

This work addresses the critical challenge of optimal filter selection for a novel trace gas measurement device. This device uses photonic crystal filters to retrieve trace gas concentrations prone to photon and read noise. The filter selection directly influences accuracy and precision of the gas retrieval and therefore is a crucial performance driver. We formulate the problem as a stochastic combinatorial optimization problem and develop a simulator mimicking gas retrieval with noise. The objective function for selecting filters reducing retrieval error is minimized by the employed metaheuristics, that represent various families of optimizers. We aim to improve the found top-performing algorithms using our novel distance-driven extensions, that employ metrics on the space of filter selections. This leads to a novel adaptation of the UMDA algorithm, we call UMDA-U-PLS-Dist, equipped with one of the proposed distance metrics as the most efficient and robust solver among the considered ones. Analysis of filter sets produced by this method reveals that filters with relatively smooth transmission profiles but containing high contrast improve the device performance. Moreover, the top-performing obtained solution shows significant improvement compared to the baseline.

A Functional Analysis Approach to Symbolic Regression

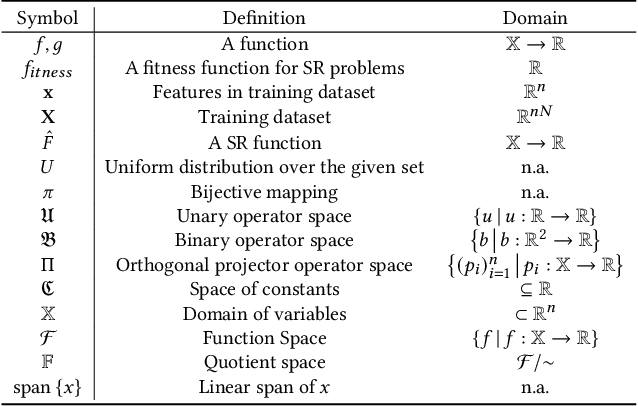
Symbolic regression (SR) poses a significant challenge for randomized search heuristics due to its reliance on the synthesis of expressions for input-output mappings. Although traditional genetic programming (GP) algorithms have achieved success in various domains, they exhibit limited performance when tree-based representations are used for SR. To address these limitations, we introduce a novel SR approach called Fourier Tree Growing (FTG) that draws insights from functional analysis. This new perspective enables us to perform optimization directly in a different space, thus avoiding intricate symbolic expressions. Our proposed algorithm exhibits significant performance improvements over traditional GP methods on a range of classical one-dimensional benchmarking problems. To identify and explain limiting factors of GP and FTG, we perform experiments on a large-scale polynomials benchmark with high-order polynomials up to degree 100. To the best of the authors' knowledge, this work represents the pioneering application of functional analysis in addressing SR problems. The superior performance of the proposed algorithm and insights into the limitations of GP open the way for further advancing GP for SR and related areas of explainable machine learning.

Representation-agnostic distance-driven perturbation for optimizing ill-conditioned problems

Locality is a crucial property for efficiently optimising black-box problems with randomized search heuristics. However, in practical applications, it is not likely to always find such a genotype encoding of candidate solutions that this property is upheld with respect to the Hamming distance. At the same time, it may be possible to use domain-specific knowledge to define a metric with locality property. We propose two mutation operators to solve such optimization problems more efficiently using the metric. The first operator assumes prior knowledge about the distance, the second operator uses the distance as a black box. Those operators apply an estimation of distribution algorithm to find the best mutant according to the defined in the paper function, which employs the given distance. For pseudo-boolean and integer optimization problems, we experimentally show that both mutation operators speed up the search on most of the functions when applied in considered evolutionary algorithms and random local search. Moreover, those operators can be applied in any randomized search heuristic which uses perturbations. However, our mutation operators increase wall-clock time and so are helpful in practice when distance is (much) cheaper to compute than the real objective function.

High Dimensional Bayesian Optimization with Kernel Principal Component Analysis

Bayesian Optimization (BO) is a surrogate-based global optimization strategy that relies on a Gaussian Process regression (GPR) model to approximate the objective function and an acquisition function to suggest candidate points. It is well-known that BO does not scale well for high-dimensional problems because the GPR model requires substantially more data points to achieve sufficient accuracy and acquisition optimization becomes computationally expensive in high dimensions. Several recent works aim at addressing these issues, e.g., methods that implement online variable selection or conduct the search on a lower-dimensional sub-manifold of the original search space. Advancing our previous work of PCA-BO that learns a linear sub-manifold, this paper proposes a novel kernel PCA-assisted BO (KPCA-BO) algorithm, which embeds a non-linear sub-manifold in the search space and performs BO on this sub-manifold. Intuitively, constructing the GPR model on a lower-dimensional sub-manifold helps improve the modeling accuracy without requiring much more data from the objective function. Also, our approach defines the acquisition function on the lower-dimensional sub-manifold, making the acquisition optimization more manageable. We compare the performance of KPCA-BO to the vanilla BO and PCA-BO on the multi-modal problems of the COCO/BBOB benchmark suite. Empirical results show that KPCA-BO outperforms BO in terms of convergence speed on most test problems, and this benefit becomes more significant when the dimensionality increases. For the 60D functions, KPCA-BO surpasses PCA-BO in many test cases. Moreover, it efficiently reduces the CPU time required to train the GPR model and optimize the acquisition function compared to the vanilla BO.

Blending Dynamic Programming with Monte Carlo Simulation for Bounding the Running Time of Evolutionary Algorithms

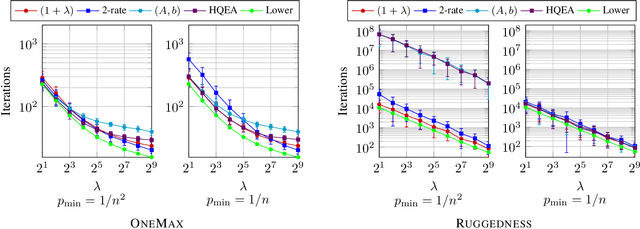
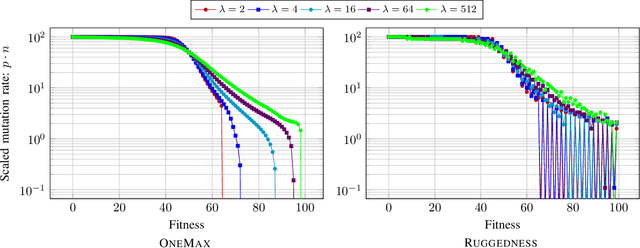
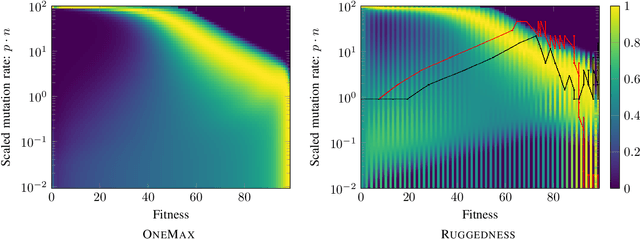
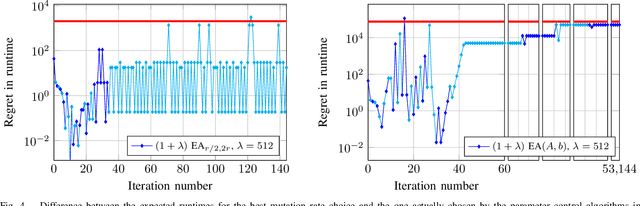
With the goal to provide absolute lower bounds for the best possible running times that can be achieved by $(1+\lambda)$-type search heuristics on common benchmark problems, we recently suggested a dynamic programming approach that computes optimal expected running times and the regret values inferred when deviating from the optimal parameter choice. Our previous work is restricted to problems for which transition probabilities between different states can be expressed by relatively simple mathematical expressions. With the goal to cover broader sets of problems, we suggest in this work an extension of the dynamic programming approach to settings in which the transition probabilities cannot necessarily be computed exactly, but in which they can be approximated numerically, up to arbitrary precision, by Monte Carlo sampling. We apply our hybrid Monte Carlo dynamic programming approach to a concatenated jump function and demonstrate how the obtained bounds can be used to gain a deeper understanding into parameter control schemes.

Offspring Population Size Matters when Comparing Evolutionary Algorithms with Self-Adjusting Mutation Rates

We analyze the performance of the 2-rate $(1+\lambda)$ Evolutionary Algorithm (EA) with self-adjusting mutation rate control, its 3-rate counterpart, and a $(1+\lambda)$~EA variant using multiplicative update rules on the OneMax problem. We compare their efficiency for offspring population sizes ranging up to $\lambda=3,200$ and problem sizes up to $n=100,000$. Our empirical results show that the ranking of the algorithms is very consistent across all tested dimensions, but strongly depends on the population size. While for small values of $\lambda$ the 2-rate EA performs best, the multiplicative updates become superior for starting for some threshold value of $\lambda$ between 50 and 100. Interestingly, for population sizes around 50, the $(1+\lambda)$~EA with static mutation rates performs on par with the best of the self-adjusting algorithms. We also consider how the lower bound $p_{\min}$ for the mutation rate influences the efficiency of the algorithms. We observe that for the 2-rate EA and the EA with multiplicative update rules the more generous bound $p_{\min}=1/n^2$ gives better results than $p_{\min}=1/n$ when $\lambda$ is small. For both algorithms the situation reverses for large~$\lambda$.