A Functional Analysis Approach to Symbolic Regression

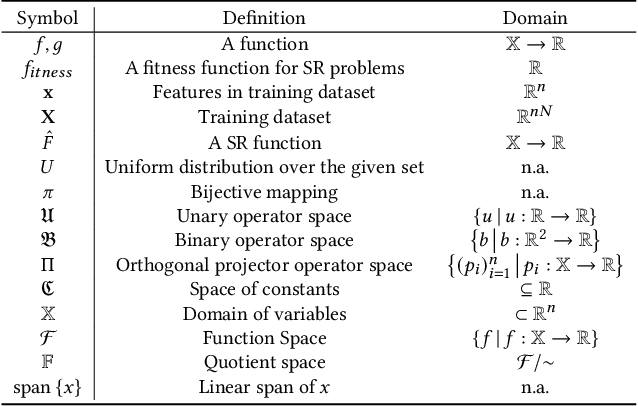
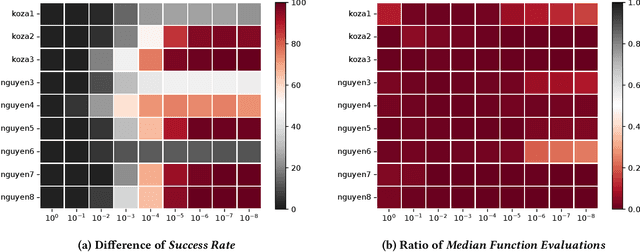
Symbolic regression (SR) poses a significant challenge for randomized search heuristics due to its reliance on the synthesis of expressions for input-output mappings. Although traditional genetic programming (GP) algorithms have achieved success in various domains, they exhibit limited performance when tree-based representations are used for SR. To address these limitations, we introduce a novel SR approach called Fourier Tree Growing (FTG) that draws insights from functional analysis. This new perspective enables us to perform optimization directly in a different space, thus avoiding intricate symbolic expressions. Our proposed algorithm exhibits significant performance improvements over traditional GP methods on a range of classical one-dimensional benchmarking problems. To identify and explain limiting factors of GP and FTG, we perform experiments on a large-scale polynomials benchmark with high-order polynomials up to degree 100. To the best of the authors' knowledge, this work represents the pioneering application of functional analysis in addressing SR problems. The superior performance of the proposed algorithm and insights into the limitations of GP open the way for further advancing GP for SR and related areas of explainable machine learning.

Challenges of ELA-guided Function Evolution using Genetic Programming

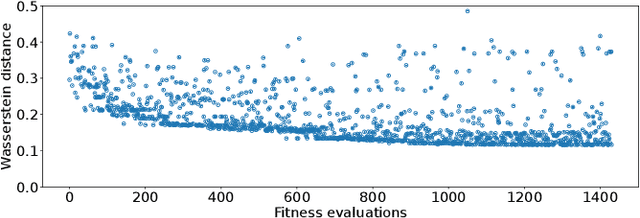
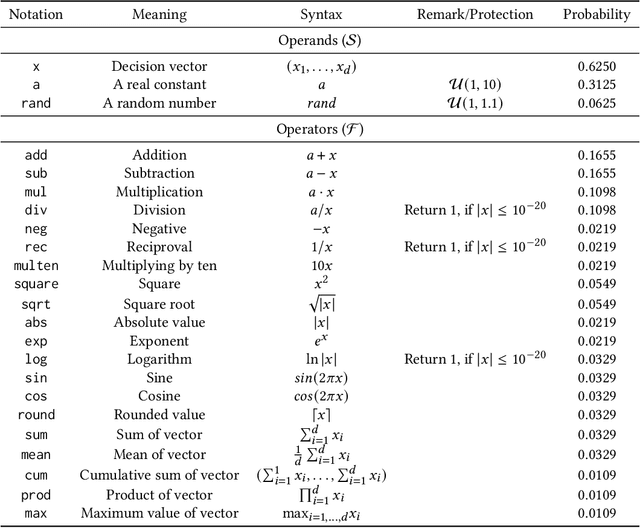
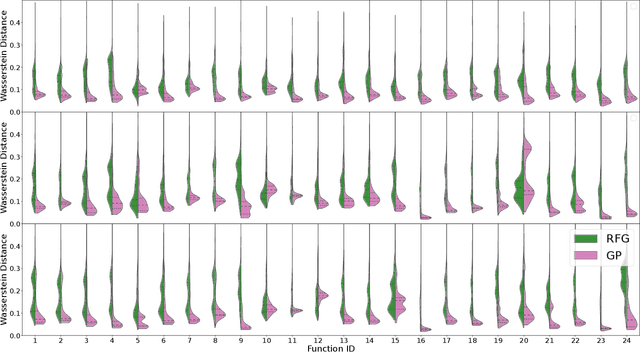
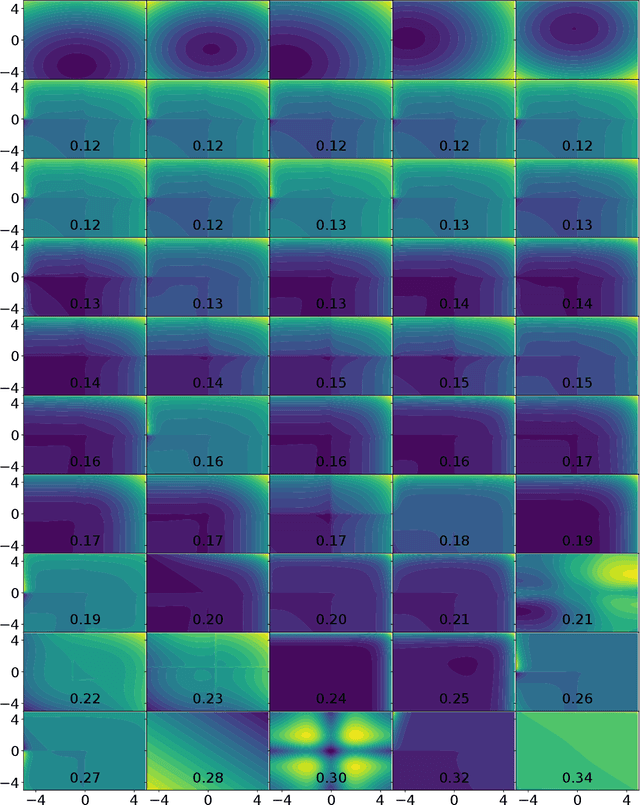
Within the optimization community, the question of how to generate new optimization problems has been gaining traction in recent years. Within topics such as instance space analysis (ISA), the generation of new problems can provide new benchmarks which are not yet explored in existing research. Beyond that, this function generation can also be exploited for solving complex real-world optimization problems. By generating functions with similar properties to the target problem, we can create a robust test set for algorithm selection and configuration. However, the generation of functions with specific target properties remains challenging. While features exist to capture low-level landscape properties, they might not always capture the intended high-level features. We show that a genetic programming (GP) approach guided by these exploratory landscape analysis (ELA) properties is not always able to find satisfying functions. Our results suggest that careful considerations of the weighting of landscape properties, as well as the distance measure used, might be required to evolve functions that are sufficiently representative to the target landscape.

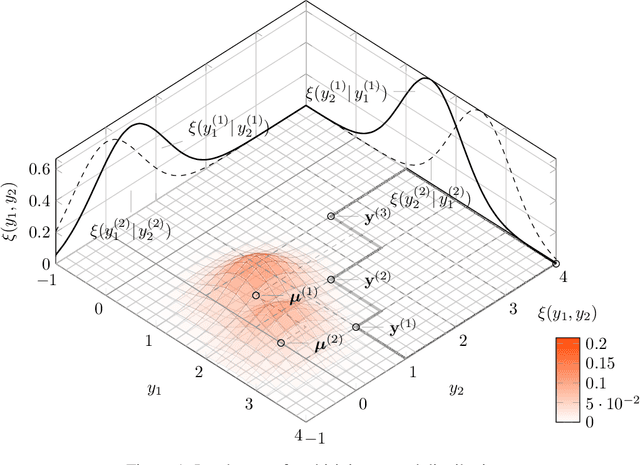
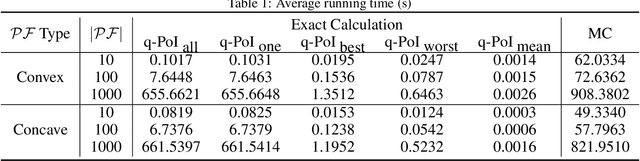
A Parallel Technique for Multi-objective Bayesian Global Optimization: Using a Batch Selection of Probability of Improvement

Bayesian global optimization (BGO) is an efficient surrogate-assisted technique for problems involving expensive evaluations. A parallel technique can be used to parallelly evaluate the true-expensive objective functions in one iteration to boost the execution time. An effective and straightforward approach is to design an acquisition function that can evaluate the performance of a bath of multiple solutions, instead of a single point/solution, in one iteration. This paper proposes five alternatives of \emph{Probability of Improvement} (PoI) with multiple points in a batch (q-PoI) for multi-objective Bayesian global optimization (MOBGO), taking the covariance among multiple points into account. Both exact computational formulas and the Monte Carlo approximation algorithms for all proposed q-PoIs are provided. Based on the distribution of the multiple points relevant to the Pareto-front, the position-dependent behavior of the five q-PoIs is investigated. Moreover, the five q-PoIs are compared with the other nine state-of-the-art and recently proposed batch MOBGO algorithms on twenty bio-objective benchmarks. The empirical experiments on different variety of benchmarks are conducted to demonstrate the effectiveness of two greedy q-PoIs ($\kpoi_{\mbox{best}}$ and $\kpoi_{\mbox{all}}$) on low-dimensional problems and the effectiveness of two explorative q-PoIs ($\kpoi_{\mbox{one}}$ and $\kpoi_{\mbox{worst}}$) on high-dimensional problems with difficult-to-approximate Pareto front boundaries.

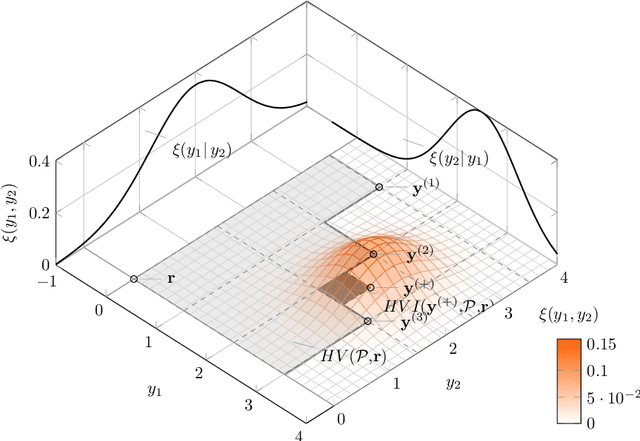
Probability Distribution of Hypervolume Improvement in Bi-objective Bayesian Optimization

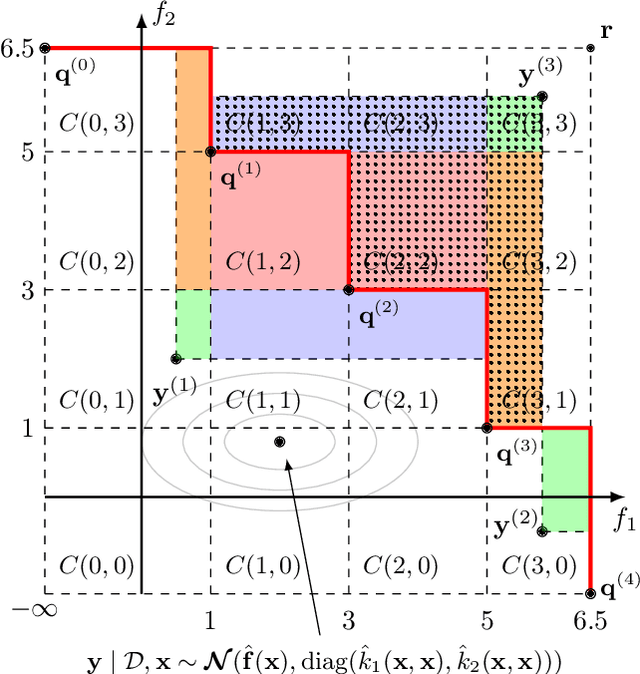
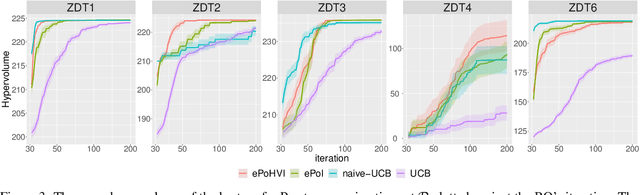
This work provides the exact expression of the probability distribution of the hypervolume improvement (HVI) for bi-objective generalization of Bayesian optimization. Here, instead of a single-objective improvement, we consider the improvement of the hypervolume indicator concerning the current best approximation of the Pareto front. Gaussian process regression models are trained independently on both objective functions, resulting in a bi-variate separated Gaussian distribution serving as a predictive model for the vector-valued objective function. Some commonly HVI-based acquisition functions (probability of improvement and upper confidence bound) are also leveraged with the help of the exact distribution of HVI. In addition, we show the superior numerical accuracy and efficiency of the exact distribution compared to the commonly used approximation by Monte-Carlo sampling. Finally, we benchmark distribution-leveraged acquisition functions on the widely applied ZDT problem set, demonstrating a significant advantage of using the exact distribution of HVI in multi-objective Bayesian optimization.

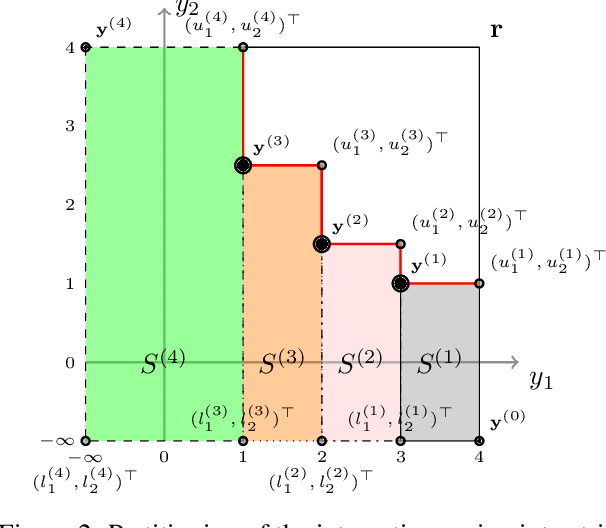
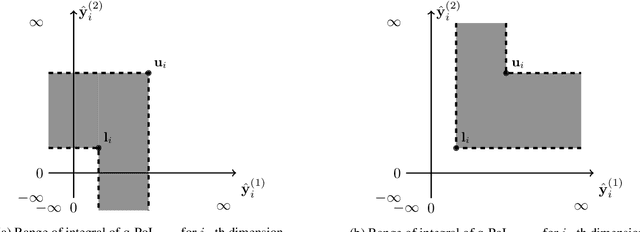
Efficient Computation of Expected Hypervolume Improvement Using Box Decomposition Algorithms

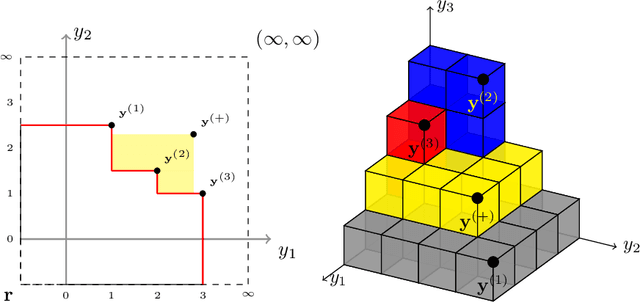
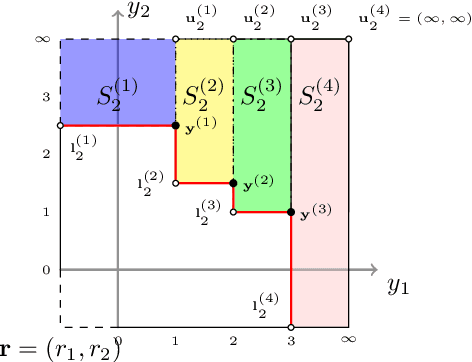
In the field of multi-objective optimization algorithms, multi-objective Bayesian Global Optimization (MOBGO) is an important branch, in addition to evolutionary multi-objective optimization algorithms (EMOAs). MOBGO utilizes Gaussian Process Models learned from previous objective function evaluations to decide the next evaluation site by maximizing or minimizing an infill criterion. A common criterion in MOBGO is the Expected Hypervolume Improvement (EHVI), which shows a good performance on a wide range of problems, with respect to exploration and exploitation. However, so far it has been a challenge to calculate exact EHVI values efficiently. In this paper, an efficient algorithm for the computation of the exact EHVI for a generic case is proposed. This efficient algorithm is based on partitioning the integration volume into a set of axis-parallel slices. Theoretically, the upper bound time complexities are improved from previously $O (n^2)$ and $O(n^3)$, for two- and three-objective problems respectively, to $\Theta(n\log n)$, which is asymptotically optimal. This article generalizes the scheme in higher dimensional case by utilizing a new hyperbox decomposition technique, which was proposed by D{\"a}chert et al, EJOR, 2017. It also utilizes a generalization of the multilayered integration scheme that scales linearly in the number of hyperboxes of the decomposition. The speed comparison shows that the proposed algorithm in this paper significantly reduces computation time. Finally, this decomposition technique is applied in the calculation of the Probability of Improvement (PoI).