How Sequential Algorithm Portfolios can benefit Black Box Optimization

In typical black-box optimization applications, the available computational budget is often allocated to a single algorithm, typically chosen based on user preference with limited knowledge about the problem at hand or according to some expert knowledge. However, we show that splitting the budget across several algorithms yield significantly better results. This approach benefits from both algorithm complementarity across diverse problems and variance reduction within individual functions, and shows that algorithm portfolios do NOT require parallel evaluation capabilities. To demonstrate the advantage of sequential algorithm portfolios, we apply it to the COCO data archive, using over 200 algorithms evaluated on the BBOB test suite. The proposed sequential portfolios consistently outperform single-algorithm baselines, achieving relative performance gains of over 14%, and offering new insights into restart mechanisms and potential for warm-started execution strategies.

Benchmarking that Matters: Rethinking Benchmarking for Practical Impact

Benchmarking has driven scientific progress in Evolutionary Computation, yet current practices fall short of real-world needs. Widely used synthetic suites such as BBOB and CEC isolate algorithmic phenomena but poorly reflect the structure, constraints, and information limitations of continuous and mixed-integer optimization problems in practice. This disconnect leads to the misuse of benchmarking suites for competitions, automated algorithm selection, and industrial decision-making, despite these suites being designed for different purposes. We identify key gaps in current benchmarking practices and tooling, including limited availability of real-world-inspired problems, missing high-level features, and challenges in multi-objective and noisy settings. We propose a vision centered on curated real-world-inspired benchmarks, practitioner-accessible feature spaces and community-maintained performance databases. Real progress requires coordinated effort: A living benchmarking ecosystem that evolves with real-world insights and supports both scientific understanding and industrial use.

A Standardized Benchmark Set of Clustering Problem Instances for Comparing Black-Box Optimizers

One key challenge in optimization is the selection of a suitable set of benchmark problems. A common goal is to find functions which are representative of a class of real-world optimization problems in order to ensure findings on the benchmarks will translate to relevant problem domains. While some problem characteristics are well-covered by popular benchmarking suites, others are often overlooked. One example of such a problem characteristic is permutation invariance, where the search space consists of a set of symmetrical search regions. This type of problem occurs e.g. when a set of solutions has to be found, but the ordering within this set does not matter. The data clustering problem, often seen in machine learning contexts, is a clear example of such an optimization landscape, and has thus been proposed as a base from which optimization benchmarks can be created. In addition to the symmetry aspect, these clustering problems also contain potential regions of neutrality, which can provide an additional challenge to optimization algorithms. In this paper, we present a standardized benchmark suite for the evaluation of continuous black-box optimization algorithms, based on data clustering problems. To gain insight into the diversity of the benchmark set, both internally and in comparison to existing suites, we perform a benchmarking study of a set of modular CMA-ES configurations, as well as an analysis using exploratory landscape analysis. Our benchmark set is open-source and integrated with the IOHprofiler benchmarking framework to encourage its use in future research.

Abnormal Mutations: Evolution Strategies Don't Require Gaussianity

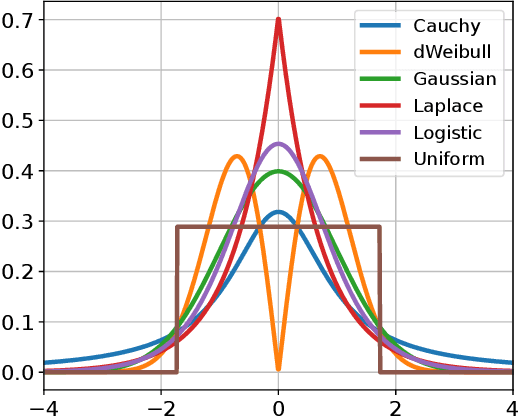
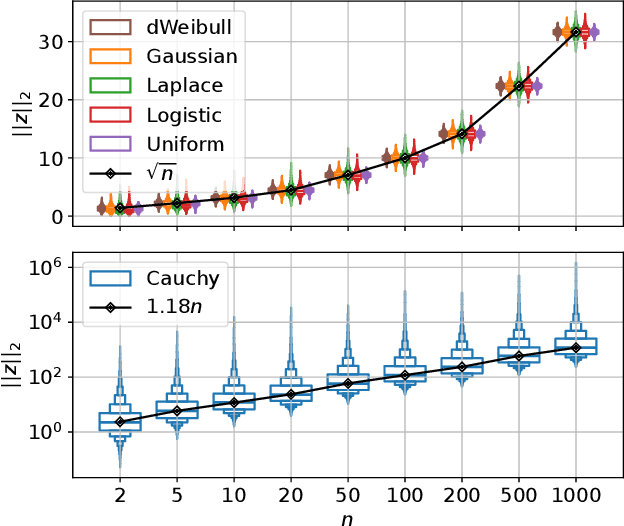
The mutation process in evolution strategies has been interlinked with the normal distribution since its inception. Many lines of reasoning have been given for this strong dependency, ranging from maximum entropy arguments to the need for isotropy. However, some theoretical results suggest that other distributions might lead to similar local convergence properties. This paper empirically shows that a wide range of evolutionary strategies, from the (1+1)-ES to CMA-ES, show comparable optimization performance when using a mutation distribution other than the standard Gaussian. Replacing it with, e.g., uniformly distributed mutations, does not deteriorate the performance of ES, when using the default adaptation mechanism for the strategy parameters. We observe that these results hold not only for the sphere model but also for a wider range of benchmark problems.

Transfer Learning of Surrogate Models: Integrating Domain Warping and Affine Transformations

Surrogate models provide efficient alternatives to computationally demanding real-world processes but often require large datasets for effective training. A promising solution to this limitation is the transfer of pre-trained surrogate models to new tasks. Previous studies have investigated the transfer of differentiable and non-differentiable surrogate models, typically assuming an affine transformation between the source and target functions. This paper extends previous research by addressing a broader range of transformations, including linear and nonlinear variations. Specifically, we consider the combination of an unknown input warping, such as one modelled by the beta cumulative distribution function, with an unspecified affine transformation. Our approach achieves transfer learning by employing a limited number of data points from the target task to optimize these transformations, minimizing empirical loss on the transfer dataset. We validate the proposed method on the widely used Black-Box Optimization Benchmark (BBOB) testbed and a real-world transfer learning task from the automobile industry. The results underscore the significant advantages of the approach, revealing that the transferred surrogate significantly outperforms both the original surrogate and the one built from scratch using the transfer dataset, particularly in data-scarce scenarios.

Transfer Learning of Surrogate Models via Domain Affine Transformation Across Synthetic and Real-World Benchmarks

Surrogate models are frequently employed as efficient substitutes for the costly execution of real-world processes. However, constructing a high-quality surrogate model often demands extensive data acquisition. A solution to this issue is to transfer pre-trained surrogate models for new tasks, provided that certain invariances exist between tasks. This study focuses on transferring non-differentiable surrogate models (e.g., random forest) from a source function to a target function, where we assume their domains are related by an unknown affine transformation, using only a limited amount of transfer data points evaluated on the target. Previous research attempts to tackle this challenge for differentiable models, e.g., Gaussian process regression, which minimizes the empirical loss on the transfer data by tuning the affine transformations. In this paper, we extend the previous work to the random forest model and assess its effectiveness on a widely-used artificial problem set - Black-Box Optimization Benchmark (BBOB) testbed, and on four real-world transfer learning problems. The results highlight the significant practical advantages of the proposed method, particularly in reducing both the data requirements and computational costs of training surrogate models for complex real-world scenarios.

Stalling in Space: Attractor Analysis for any Algorithm

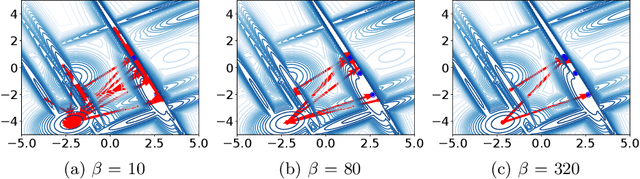
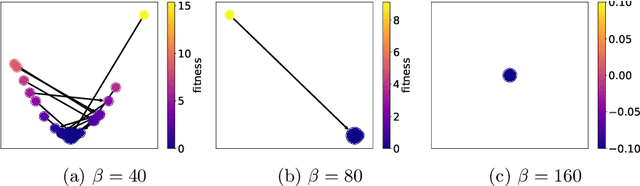
Network-based representations of fitness landscapes have grown in popularity in the past decade; this is probably because of growing interest in explainability for optimisation algorithms. Local optima networks (LONs) have been especially dominant in the literature and capture an approximation of local optima and their connectivity in the landscape. However, thus far, LONs have been constructed according to a strict definition of what a local optimum is: the result of local search. Many evolutionary approaches do not include this, however. Popular algorithms such as CMA-ES have therefore never been subject to LON analysis. Search trajectory networks (STNs) offer a possible alternative: nodes can be any search space location. However, STNs are not typically modelled in such a way that models temporal stalls: that is, a region in the search space where an algorithm fails to find a better solution over a defined period of time. In this work, we approach this by systematically analysing a special case of STN which we name attractor networks. These offer a coarse-grained view of algorithm behaviour with a singular focus on stall locations. We construct attractor networks for CMA-ES, differential evolution, and random search for 24 noiseless black-box optimisation benchmark problems. The properties of attractor networks are systematically explored. They are also visualised and compared to traditional LONs and STN models. We find that attractor networks facilitate insights into algorithm behaviour which other models cannot, and we advocate for the consideration of attractor analysis even for algorithms which do not include local search.

MO-IOHinspector: Anytime Benchmarking of Multi-Objective Algorithms using IOHprofiler

Benchmarking is one of the key ways in which we can gain insight into the strengths and weaknesses of optimization algorithms. In sampling-based optimization, considering the anytime behavior of an algorithm can provide valuable insights for further developments. In the context of multi-objective optimization, this anytime perspective is not as widely adopted as in the single-objective context. In this paper, we propose a new software tool which uses principles from unbounded archiving as a logging structure. This leads to a clearer separation between experimental design and subsequent analysis decisions. We integrate this approach as a new Python module into the IOHprofiler framework and demonstrate the benefits of this approach by showcasing the ability to change indicators, aggregations, and ranking procedures during the analysis pipeline.

Sampling in CMA-ES: Low Numbers of Low Discrepancy Points

The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is one of the most successful examples of a derandomized evolution strategy. However, it still relies on randomly sampling offspring, which can be done via a uniform distribution and subsequently transforming into the required Gaussian. Previous work has shown that replacing this uniform sampling with a low-discrepancy sampler, such as Halton or Sobol sequences, can improve performance over a wide set of problems. We show that iterating through small, fixed sets of low-discrepancy points can still perform better than the default uniform distribution. Moreover, using only 128 points throughout the search is sufficient to closely approximate the empirical performance of using the complete pseudorandom sequence up to dimensionality 40 on the BBOB benchmark. For lower dimensionalities (below 10), we find that using as little as 32 unique low discrepancy points performs similar or better than uniform sampling. In 2D, for which we have highly optimized low discrepancy samples available, we demonstrate that using these points yields the highest empirical performance and requires only 16 samples to improve over uniform sampling. Overall, we establish a clear relation between the $L_2$ discrepancy of the used point set and the empirical performance of the CMA-ES.

Quantifying Individual and Joint Module Impact in Modular Optimization Frameworks

This study explores the influence of modules on the performance of modular optimization frameworks for continuous single-objective black-box optimization. There is an extensive variety of modules to choose from when designing algorithm variants, however, there is a rather limited understanding of how each module individually influences the algorithm performance and how the modules interact with each other when combined. We use the functional ANOVA (f-ANOVA) framework to quantify the influence of individual modules and module combinations for two algorithms, the modular Covariance Matrix Adaptation (modCMA) and the modular Differential Evolution (modDE). We analyze the performance data from 324 modCMA and 576 modDE variants on the BBOB benchmark collection, for two problem dimensions, and three computational budgets. Noteworthy findings include the identification of important modules that strongly influence the performance of modCMA, such as the~\textit{weights\ option} and~\textit{mirrored} modules for low dimensional problems, and the~\textit{base\ sampler} for high dimensional problems. The large individual influence of the~\textit{lpsr} module makes it very important for the performance of modDE, regardless of the problem dimensionality and the computational budget. When comparing modCMA and modDE, modDE undergoes a shift from individual modules being more influential, to module combinations being more influential, while modCMA follows the opposite pattern, with an increase in problem dimensionality and computational budget.