LLM Driven Design of Continuous Optimization Problems with Controllable High-level Properties

Benchmarking in continuous black-box optimisation is hindered by the limited structural diversity of existing test suites such as BBOB. We explore whether large language models embedded in an evolutionary loop can be used to design optimisation problems with clearly defined high-level landscape characteristics. Using the LLaMEA framework, we guide an LLM to generate problem code from natural-language descriptions of target properties, including multimodality, separability, basin-size homogeneity, search-space homogeneity and globallocal optima contrast. Inside the loop we score candidates through ELA-based property predictors. We introduce an ELA-space fitness-sharing mechanism that increases population diversity and steers the generator away from redundant landscapes. A complementary basin-of-attraction analysis, statistical testing and visual inspection, verifies that many of the generated functions indeed exhibit the intended structural traits. In addition, a t-SNE embedding shows that they expand the BBOB instance space rather than forming an unrelated cluster. The resulting library provides a broad, interpretable, and reproducible set of benchmark problems for landscape analysis and downstream tasks such as automated algorithm selection.

MO-ELA: Rigorously Expanding Exploratory Landscape Features for Automated Algorithm Selection in Continuous Multi-Objective Optimisation

Automated Algorithm Selection (AAS) is a popular meta-algorithmic approach and has demonstrated to work well for single-objective optimisation in combination with exploratory landscape features (ELA), i.e., (numerical) descriptive features derived from sampling the black-box (continuous) optimisation problem. In contrast to the abundance of features that describe single-objective optimisation problems, only a few features have been proposed for multi-objective optimisation so far. Building upon recent work on exploratory landscape features for box-constrained continuous multi-objective optimization problems, we propose a novel and complementary set of additional features (MO-ELA). These features are based on a random sample of points considering both the decision and objective space. The features are divided into 5 feature groups depending on how they are being calculated: non-dominated-sorting, descriptive statistics, principal component analysis, graph structures and gradient information. An AAS study conducted on well-established multi-objective benchmarks demonstrates that the proposed features contribute to successfully distinguishing between algorithm performance and thus adequately capture problem hardness resulting in models that come very close to the virtual best solver. After feature selection, the newly proposed features are frequently among the top contributors, underscoring their value in algorithm selection and problem characterisation.

Best Practices For Empirical Meta-Algorithmic Research: Guidelines from the COSEAL Research Network

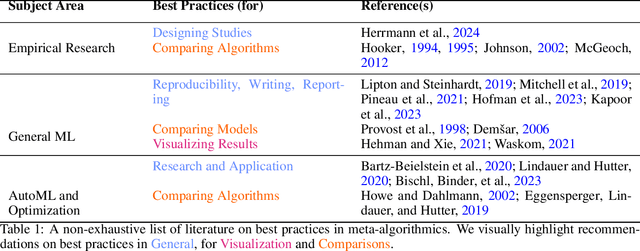
Empirical research on meta-algorithmics, such as algorithm selection, configuration, and scheduling, often relies on extensive and thus computationally expensive experiments. With the large degree of freedom we have over our experimental setup and design comes a plethora of possible error sources that threaten the scalability and validity of our scientific insights. Best practices for meta-algorithmic research exist, but they are scattered between different publications and fields, and continue to evolve separately from each other. In this report, we collect good practices for empirical meta-algorithmic research across the subfields of the COSEAL community, encompassing the entire experimental cycle: from formulating research questions and selecting an experimental design, to executing experiments, and ultimately, analyzing and presenting results impartially. It establishes the current state-of-the-art practices within meta-algorithmic research and serves as a guideline to both new researchers and practitioners in meta-algorithmic fields.

MO-IOHinspector: Anytime Benchmarking of Multi-Objective Algorithms using IOHprofiler

Benchmarking is one of the key ways in which we can gain insight into the strengths and weaknesses of optimization algorithms. In sampling-based optimization, considering the anytime behavior of an algorithm can provide valuable insights for further developments. In the context of multi-objective optimization, this anytime perspective is not as widely adopted as in the single-objective context. In this paper, we propose a new software tool which uses principles from unbounded archiving as a logging structure. This leads to a clearer separation between experimental design and subsequent analysis decisions. We integrate this approach as a new Python module into the IOHprofiler framework and demonstrate the benefits of this approach by showcasing the ability to change indicators, aggregations, and ranking procedures during the analysis pipeline.

Hybridizing Target- and SHAP-encoded Features for Algorithm Selection in Mixed-variable Black-box Optimization

Exploratory landscape analysis (ELA) is a well-established tool to characterize optimization problems via numerical features. ELA is used for problem comprehension, algorithm design, and applications such as automated algorithm selection and configuration. Until recently, however, ELA was limited to search spaces with either continuous or discrete variables, neglecting problems with mixed variable types. This gap was addressed in a recent study that uses an approach based on target-encoding to compute exploratory landscape features for mixedvariable problems. In this work, we investigate an alternative encoding scheme based on SHAP values. While these features do not lead to better results in the algorithm selection setting considered in previous work, the two different encoding mechanisms exhibit complementary performance. Combining both feature sets into a hybrid approach outperforms each encoding mechanism individually. Finally, we experiment with two different ways of meta-selecting between the two feature sets. Both approaches are capable of taking advantage of the performance complementarity of the models trained on target-encoded and SHAP-encoded feature sets, respectively.

Exploratory Landscape Analysis for Mixed-Variable Problems

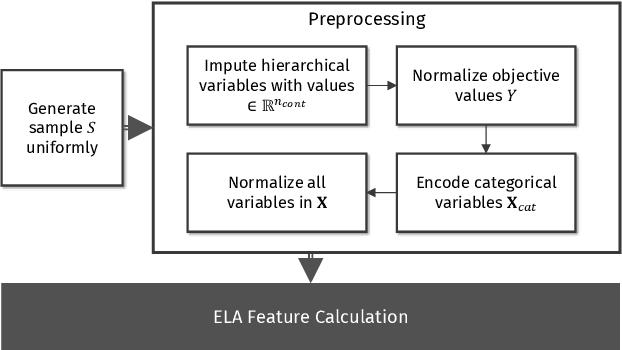
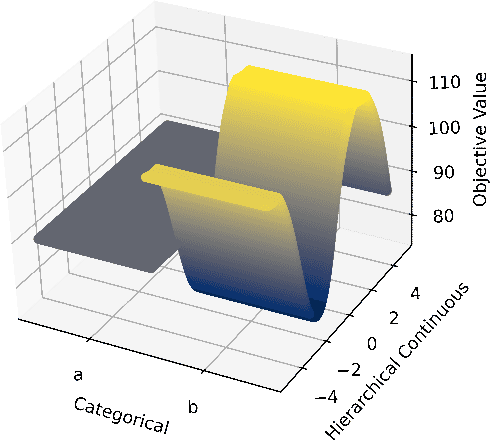
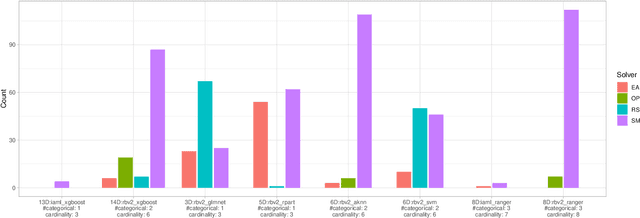
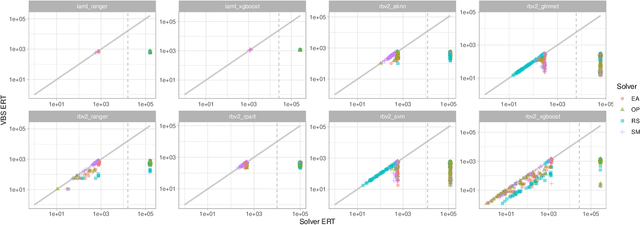
Exploratory landscape analysis and fitness landscape analysis in general have been pivotal in facilitating problem understanding, algorithm design and endeavors such as automated algorithm selection and configuration. These techniques have largely been limited to search spaces of a single domain. In this work, we provide the means to compute exploratory landscape features for mixed-variable problems where the decision space is a mixture of continuous, binary, integer, and categorical variables. This is achieved by utilizing existing encoding techniques originating from machine learning. We provide a comprehensive juxtaposition of the results based on these different techniques. To further highlight their merit for practical applications, we design and conduct an automated algorithm selection study based on a hyperparameter optimization benchmark suite. We derive a meaningful compartmentalization of these benchmark problems by clustering based on the used landscape features. The identified clusters mimic the behavior the used algorithms exhibit. Meaning, the different clusters have different best performing algorithms. Finally, our trained algorithm selector is able to close the gap between the single best and the virtual best solver by 57.5% over all benchmark problems.

Deep-ELA: Deep Exploratory Landscape Analysis with Self-Supervised Pretrained Transformers for Single- and Multi-Objective Continuous Optimization Problems

In many recent works, the potential of Exploratory Landscape Analysis (ELA) features to numerically characterize, in particular, single-objective continuous optimization problems has been demonstrated. These numerical features provide the input for all kinds of machine learning tasks on continuous optimization problems, ranging, i.a., from High-level Property Prediction to Automated Algorithm Selection and Automated Algorithm Configuration. Without ELA features, analyzing and understanding the characteristics of single-objective continuous optimization problems would be impossible. Yet, despite their undisputed usefulness, ELA features suffer from several drawbacks. These include, in particular, (1.) a strong correlation between multiple features, as well as (2.) its very limited applicability to multi-objective continuous optimization problems. As a remedy, recent works proposed deep learning-based approaches as alternatives to ELA. In these works, e.g., point-cloud transformers were used to characterize an optimization problem's fitness landscape. However, these approaches require a large amount of labeled training data. Within this work, we propose a hybrid approach, Deep-ELA, which combines (the benefits of) deep learning and ELA features. Specifically, we pre-trained four transformers on millions of randomly generated optimization problems to learn deep representations of the landscapes of continuous single- and multi-objective optimization problems. Our proposed framework can either be used out-of-the-box for analyzing single- and multi-objective continuous optimization problems, or subsequently fine-tuned to various tasks focussing on algorithm behavior and problem understanding.

HPO X ELA: Investigating Hyperparameter Optimization Landscapes by Means of Exploratory Landscape Analysis

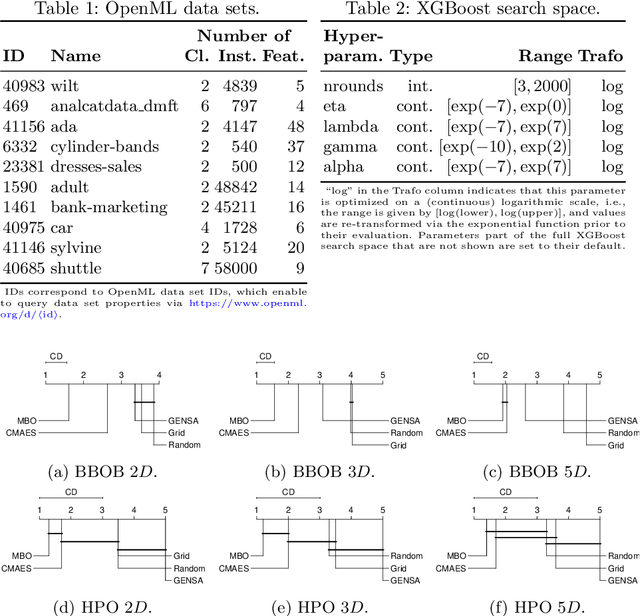
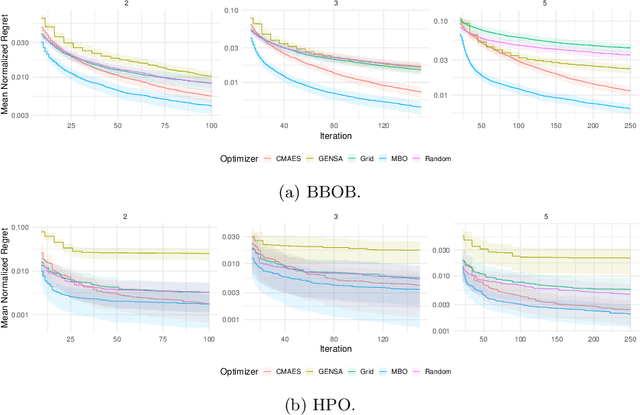
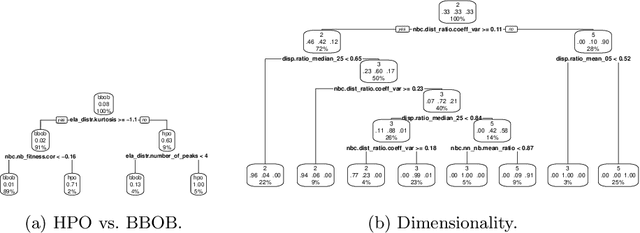
Hyperparameter optimization (HPO) is a key component of machine learning models for achieving peak predictive performance. While numerous methods and algorithms for HPO have been proposed over the last years, little progress has been made in illuminating and examining the actual structure of these black-box optimization problems. Exploratory landscape analysis (ELA) subsumes a set of techniques that can be used to gain knowledge about properties of unknown optimization problems. In this paper, we evaluate the performance of five different black-box optimizers on 30 HPO problems, which consist of two-, three- and five-dimensional continuous search spaces of the XGBoost learner trained on 10 different data sets. This is contrasted with the performance of the same optimizers evaluated on 360 problem instances from the black-box optimization benchmark (BBOB). We then compute ELA features on the HPO and BBOB problems and examine similarities and differences. A cluster analysis of the HPO and BBOB problems in ELA feature space allows us to identify how the HPO problems compare to the BBOB problems on a structural meta-level. We identify a subset of BBOB problems that are close to the HPO problems in ELA feature space and show that optimizer performance is comparably similar on these two sets of benchmark problems. We highlight open challenges of ELA for HPO and discuss potential directions of future research and applications.

A Collection of Deep Learning-based Feature-Free Approaches for Characterizing Single-Objective Continuous Fitness Landscapes

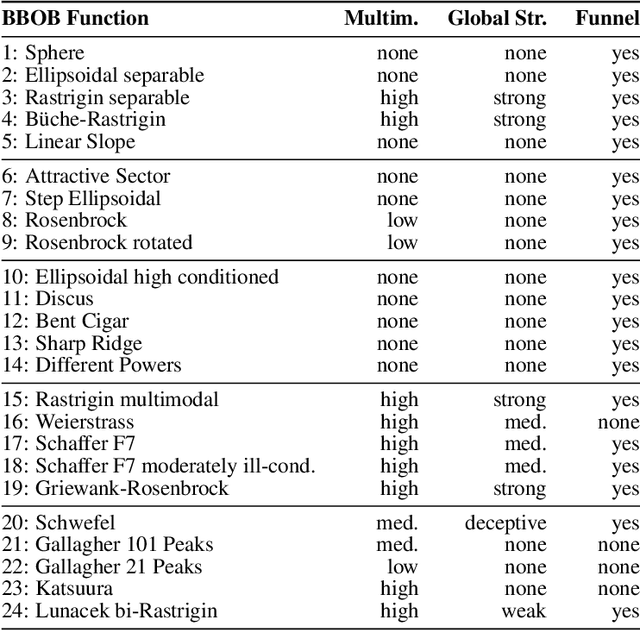
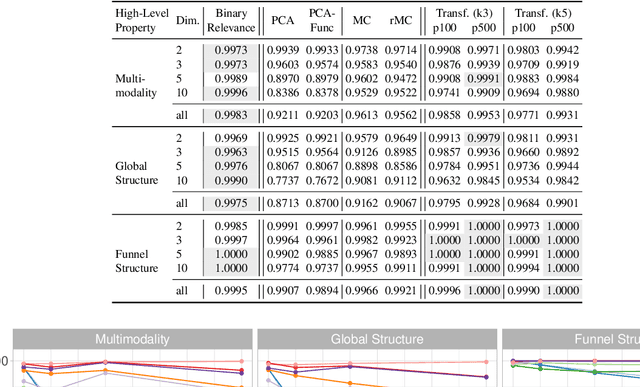
Exploratory Landscape Analysis is a powerful technique for numerically characterizing landscapes of single-objective continuous optimization problems. Landscape insights are crucial both for problem understanding as well as for assessing benchmark set diversity and composition. Despite the irrefutable usefulness of these features, they suffer from their own ailments and downsides. Hence, in this work we provide a collection of different approaches to characterize optimization landscapes. Similar to conventional landscape features, we require a small initial sample. However, instead of computing features based on that sample, we develop alternative representations of the original sample. These range from point clouds to 2D images and, therefore, are entirely feature-free. We demonstrate and validate our devised methods on the BBOB testbed and predict, with the help of Deep Learning, the high-level, expert-based landscape properties such as the degree of multimodality and the existence of funnel structures. The quality of our approaches is on par with methods relying on the traditional landscape features. Thereby, we provide an exciting new perspective on every research area which utilizes problem information such as problem understanding and algorithm design as well as automated algorithm configuration and selection.

Multiobjectivization of Local Search: Single-Objective Optimization Benefits From Multi-Objective Gradient Descent

Multimodality is one of the biggest difficulties for optimization as local optima are often preventing algorithms from making progress. This does not only challenge local strategies that can get stuck. It also hinders meta-heuristics like evolutionary algorithms in convergence to the global optimum. In this paper we present a new concept of gradient descent, which is able to escape local traps. It relies on multiobjectivization of the original problem and applies the recently proposed and here slightly modified multi-objective local search mechanism MOGSA. We use a sophisticated visualization technique for multi-objective problems to prove the working principle of our idea. As such, this work highlights the transfer of new insights from the multi-objective to the single-objective domain and provides first visual evidence that multiobjectivization can link single-objective local optima in multimodal landscapes.