Lennart Schäpermeier
Best Practices For Empirical Meta-Algorithmic Research: Guidelines from the COSEAL Research Network
Dec 19, 2025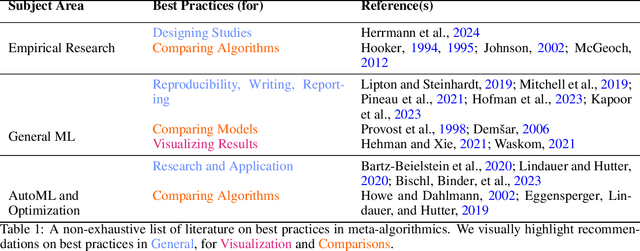
Abstract:Empirical research on meta-algorithmics, such as algorithm selection, configuration, and scheduling, often relies on extensive and thus computationally expensive experiments. With the large degree of freedom we have over our experimental setup and design comes a plethora of possible error sources that threaten the scalability and validity of our scientific insights. Best practices for meta-algorithmic research exist, but they are scattered between different publications and fields, and continue to evolve separately from each other. In this report, we collect good practices for empirical meta-algorithmic research across the subfields of the COSEAL community, encompassing the entire experimental cycle: from formulating research questions and selecting an experimental design, to executing experiments, and ultimately, analyzing and presenting results impartially. It establishes the current state-of-the-art practices within meta-algorithmic research and serves as a guideline to both new researchers and practitioners in meta-algorithmic fields.
Benchmarking that Matters: Rethinking Benchmarking for Practical Impact
Nov 15, 2025Abstract:Benchmarking has driven scientific progress in Evolutionary Computation, yet current practices fall short of real-world needs. Widely used synthetic suites such as BBOB and CEC isolate algorithmic phenomena but poorly reflect the structure, constraints, and information limitations of continuous and mixed-integer optimization problems in practice. This disconnect leads to the misuse of benchmarking suites for competitions, automated algorithm selection, and industrial decision-making, despite these suites being designed for different purposes. We identify key gaps in current benchmarking practices and tooling, including limited availability of real-world-inspired problems, missing high-level features, and challenges in multi-objective and noisy settings. We propose a vision centered on curated real-world-inspired benchmarks, practitioner-accessible feature spaces and community-maintained performance databases. Real progress requires coordinated effort: A living benchmarking ecosystem that evolves with real-world insights and supports both scientific understanding and industrial use.
Greedy Restart Schedules: A Baseline for Dynamic Algorithm Selection on Numerical Black-box Optimization Problems
Apr 15, 2025Abstract:In many optimization domains, there are multiple different solvers that contribute to the overall state-of-the-art, each performing better on some, and worse on other types of problem instances. Meta-algorithmic approaches, such as instance-based algorithm selection, configuration and scheduling, aim to close this gap by extracting the most performance possible from a set of (configurable) optimizers. In this context, the best performing individual algorithms are often hand-crafted hybrid heuristics which perform many restarts of fast local optimization approaches. However, data-driven techniques to create optimized restart schedules have not yet been extensively studied. Here, we present a simple scheduling approach that iteratively selects the algorithm performing best on the distribution of unsolved training problems at time of selection, resulting in a problem-independent solver schedule. We demonstrate our approach using well-known optimizers from numerical black-box optimization on the BBOB testbed, bridging much of the gap between single and virtual best solver from the original portfolio across various evaluation protocols. Our greedy restart schedule presents a powerful baseline for more complex dynamic algorithm selection models.
Dancing to the State of the Art? How Candidate Lists Influence LKH for Solving the Traveling Salesperson Problem
Jul 04, 2024Abstract:Solving the Traveling Salesperson Problem (TSP) remains a persistent challenge, despite its fundamental role in numerous generalized applications in modern contexts. Heuristic solvers address the demand for finding high-quality solutions efficiently. Among these solvers, the Lin-Kernighan-Helsgaun (LKH) heuristic stands out, as it complements the performance of genetic algorithms across a diverse range of problem instances. However, frequent timeouts on challenging instances hinder the practical applicability of the solver. Within this work, we investigate a previously overlooked factor contributing to many timeouts: The use of a fixed candidate set based on a tree structure. Our investigations reveal that candidate sets based on Hamiltonian circuits contain more optimal edges. We thus propose to integrate this promising initialization strategy, in the form of POPMUSIC, within an efficient restart version of LKH. As confirmed by our experimental studies, this refined TSP heuristic is much more efficient - causing fewer timeouts and improving the performance (in terms of penalized average runtime) by an order of magnitude - and thereby challenges the state of the art in TSP solving.
Reinvestigating the R2 Indicator: Achieving Pareto Compliance by Integration
Jul 01, 2024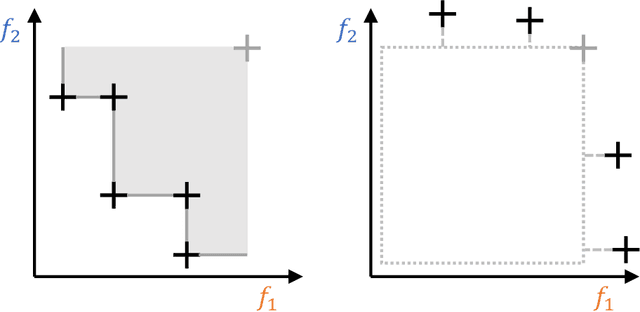


Abstract:In multi-objective optimization, set-based quality indicators are a cornerstone of benchmarking and performance assessment. They capture the quality of a set of trade-off solutions by reducing it to a scalar number. One of the most commonly used set-based metrics is the R2 indicator, which describes the expected utility of a solution set to a decision-maker under a distribution of utility functions. Typically, this indicator is applied by discretizing this distribution of utility functions, yielding a weakly Pareto-compliant indicator. In consequence, adding a nondominated or dominating solution to a solution set may - but does not have to - improve the indicator's value. In this paper, we reinvestigate the R2 indicator under the premise that we have a continuous, uniform distribution of (Tchebycheff) utility functions. We analyze its properties in detail, demonstrating that this continuous variant is indeed Pareto-compliant - that is, any beneficial solution will improve the metric's value. Additionally, we provide an efficient computational procedure to compute this metric for bi-objective problems in $\mathcal O (N \log N)$. As a result, this work contributes to the state-of-the-art Pareto-compliant unary performance metrics, such as the hypervolume indicator, offering an efficient and promising alternative.
HPO X ELA: Investigating Hyperparameter Optimization Landscapes by Means of Exploratory Landscape Analysis
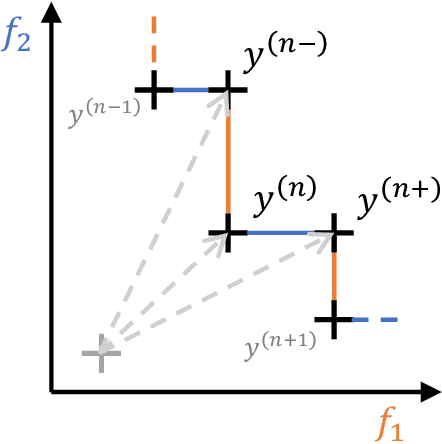
Jul 30, 2022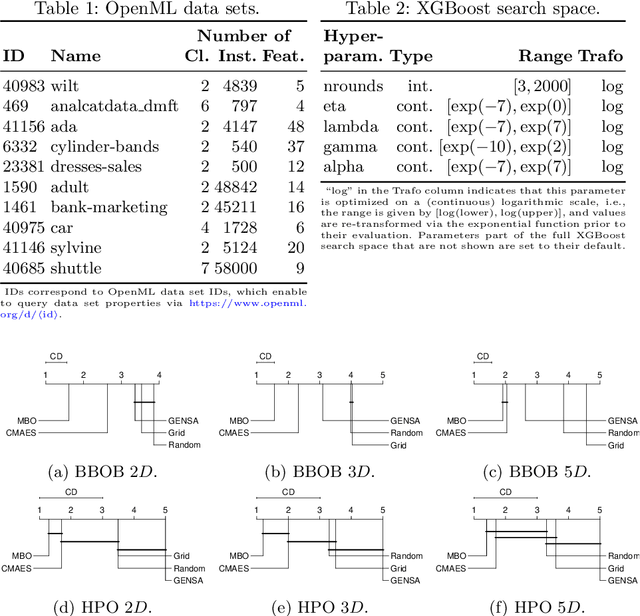
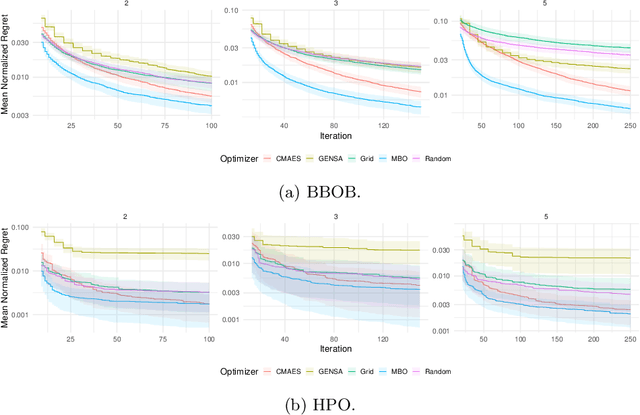

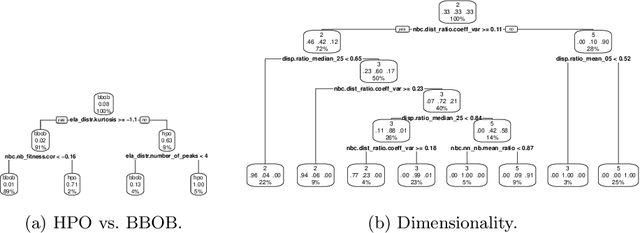
Abstract:Hyperparameter optimization (HPO) is a key component of machine learning models for achieving peak predictive performance. While numerous methods and algorithms for HPO have been proposed over the last years, little progress has been made in illuminating and examining the actual structure of these black-box optimization problems. Exploratory landscape analysis (ELA) subsumes a set of techniques that can be used to gain knowledge about properties of unknown optimization problems. In this paper, we evaluate the performance of five different black-box optimizers on 30 HPO problems, which consist of two-, three- and five-dimensional continuous search spaces of the XGBoost learner trained on 10 different data sets. This is contrasted with the performance of the same optimizers evaluated on 360 problem instances from the black-box optimization benchmark (BBOB). We then compute ELA features on the HPO and BBOB problems and examine similarities and differences. A cluster analysis of the HPO and BBOB problems in ELA feature space allows us to identify how the HPO problems compare to the BBOB problems on a structural meta-level. We identify a subset of BBOB problems that are close to the HPO problems in ELA feature space and show that optimizer performance is comparably similar on these two sets of benchmark problems. We highlight open challenges of ELA for HPO and discuss potential directions of future research and applications.
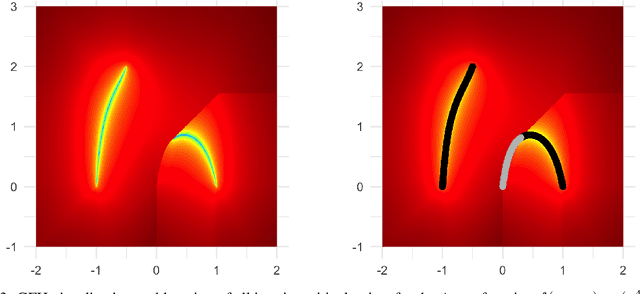
MOLE: Digging Tunnels Through Multimodal Multi-Objective Landscapes
Apr 22, 2022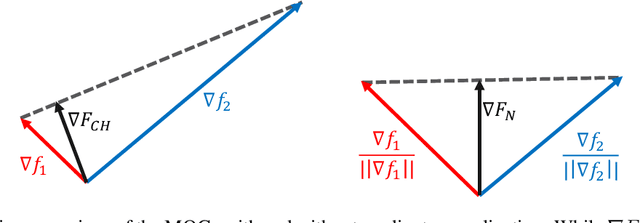
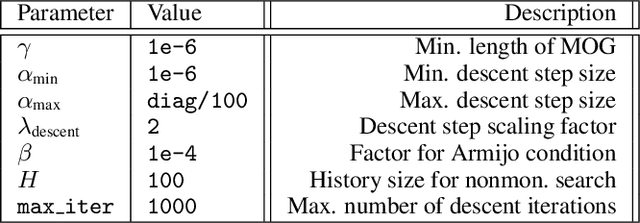
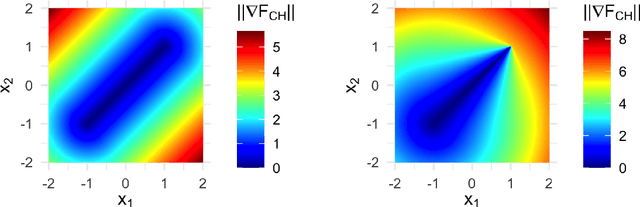

Abstract:Recent advances in the visualization of continuous multimodal multi-objective optimization (MMMOO) landscapes brought a new perspective to their search dynamics. Locally efficient (LE) sets, often considered as traps for local search, are rarely isolated in the decision space. Rather, intersections by superposing attraction basins lead to further solution sets that at least partially contain better solutions. The Multi-Objective Gradient Sliding Algorithm (MOGSA) is an algorithmic concept developed to exploit these superpositions. While it has promising performance on many MMMOO problems with linear LE sets, closer analysis of MOGSA revealed that it does not sufficiently generalize to a wider set of test problems. Based on a detailed analysis of shortcomings of MOGSA, we propose a new algorithm, the Multi-Objective Landscape Explorer (MOLE). It is able to efficiently model and exploit LE sets in MMMOO problems. An implementation of MOLE is presented for the bi-objective case, and the practicality of the approach is shown in a benchmarking experiment on the Bi-Objective BBOB testbed.
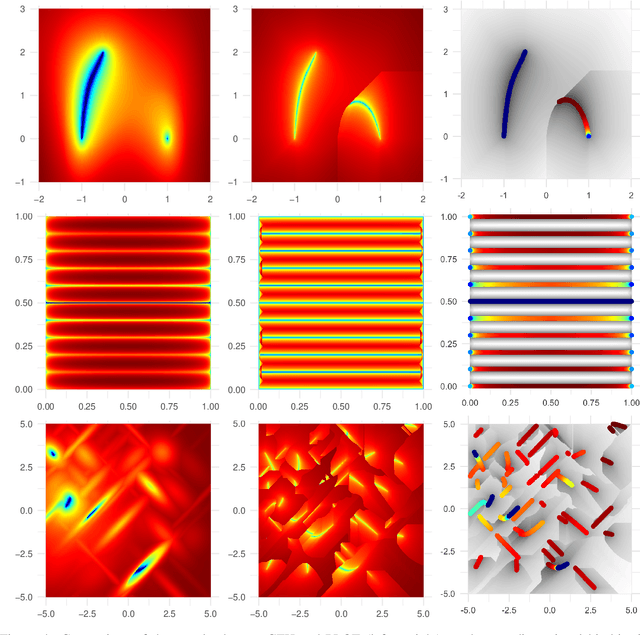
To Boldly Show What No One Has Seen Before: A Dashboard for Visualizing Multi-objective Landscapes
Nov 29, 2020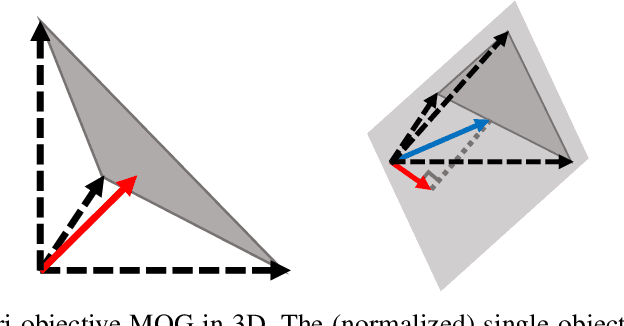
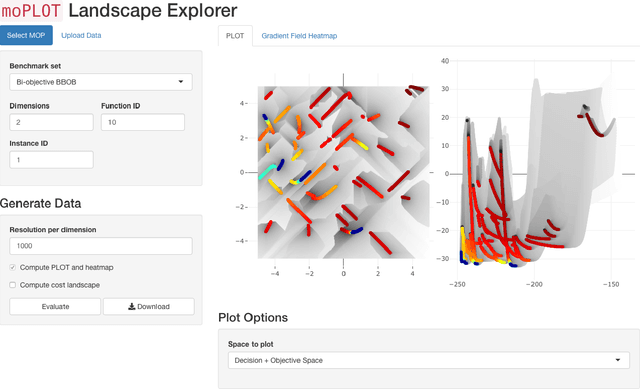
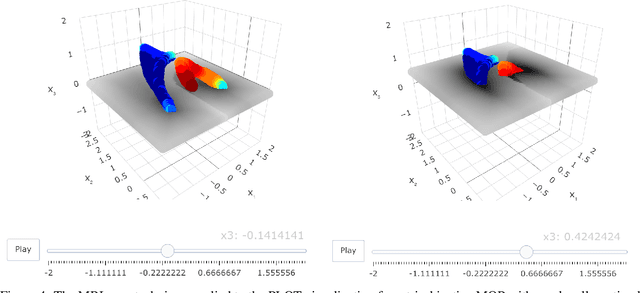
Abstract:Simultaneously visualizing the decision and objective space of continuous multi-objective optimization problems (MOPs) recently provided key contributions in understanding the structure of their landscapes. For the sake of advancing these recent findings, we compiled all state-of-the-art visualization methods in a single R-package (moPLOT). Moreover, we extended these techniques to handle three-dimensional decision spaces and propose two solutions for visualizing the resulting volume of data points. This enables - for the first time - to illustrate the landscape structures of three-dimensional MOPs. However, creating these visualizations using the aforementioned framework still lays behind a high barrier of entry for many people as it requires basic skills in R. To enable any user to create and explore MOP landscapes using moPLOT, we additionally provide a dashboard that allows to compute the state-of-the-art visualizations for a wide variety of common benchmark functions through an interactive (web-based) user interface.
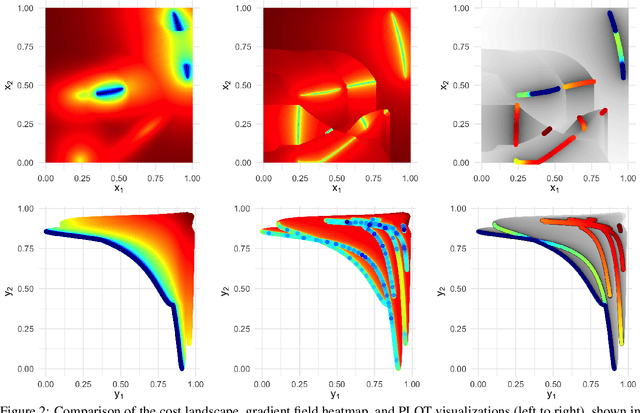
One PLOT to Show Them All: Visualization of Efficient Sets in Multi-Objective Landscapes
Jun 20, 2020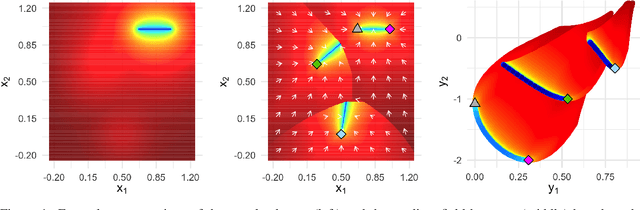
Abstract:Visualization techniques for the decision space of continuous multi-objective optimization problems (MOPs) are rather scarce in research. For long, all techniques focused on global optimality and even for the few available landscape visualizations, e.g., cost landscapes, globality is the main criterion. In contrast, the recently proposed gradient field heatmaps (GFHs) emphasize the location and attraction basins of local efficient sets, but ignore the relation of sets in terms of solution quality. In this paper, we propose a new and hybrid visualization technique, which combines the advantages of both approaches in order to represent local and global optimality together within a single visualization. Therefore, we build on the GFH approach but apply a new technique for approximating the location of locally efficient points and using the divergence of the multi-objective gradient vector field as a robust second-order condition. Then, the relative dominance relationship of the determined locally efficient points is used to visualize the complete landscape of the MOP. Augmented by information on the basins of attraction, this Plot of Landscapes with Optimal Trade-offs (PLOT) becomes one of the most informative multi-objective landscape visualization techniques available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge