Hybridizing Target- and SHAP-encoded Features for Algorithm Selection in Mixed-variable Black-box Optimization

Exploratory landscape analysis (ELA) is a well-established tool to characterize optimization problems via numerical features. ELA is used for problem comprehension, algorithm design, and applications such as automated algorithm selection and configuration. Until recently, however, ELA was limited to search spaces with either continuous or discrete variables, neglecting problems with mixed variable types. This gap was addressed in a recent study that uses an approach based on target-encoding to compute exploratory landscape features for mixedvariable problems. In this work, we investigate an alternative encoding scheme based on SHAP values. While these features do not lead to better results in the algorithm selection setting considered in previous work, the two different encoding mechanisms exhibit complementary performance. Combining both feature sets into a hybrid approach outperforms each encoding mechanism individually. Finally, we experiment with two different ways of meta-selecting between the two feature sets. Both approaches are capable of taking advantage of the performance complementarity of the models trained on target-encoded and SHAP-encoded feature sets, respectively.

Exploratory Landscape Analysis for Mixed-Variable Problems

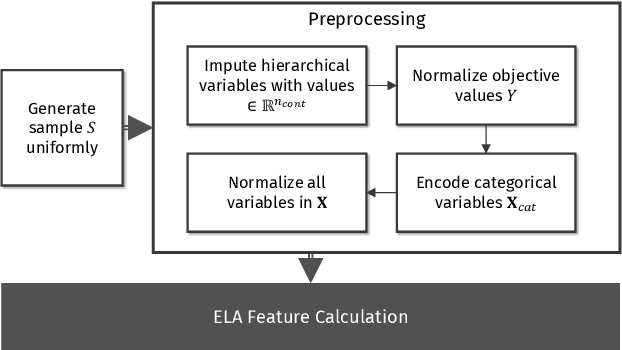
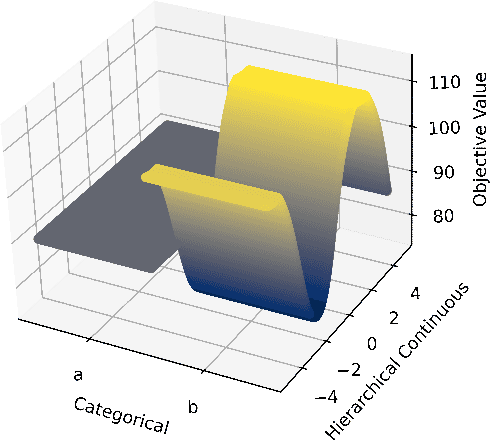
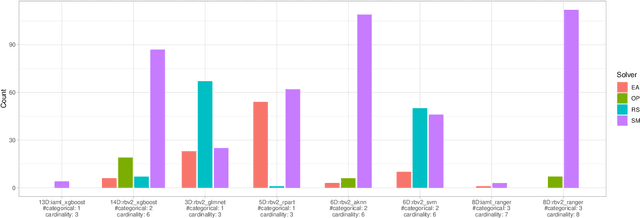
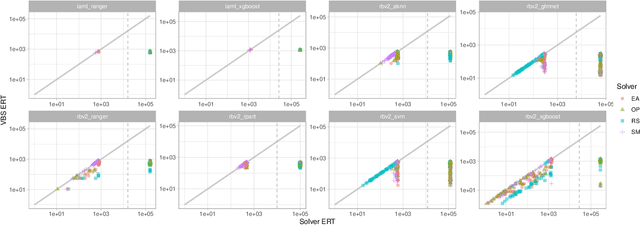
Exploratory landscape analysis and fitness landscape analysis in general have been pivotal in facilitating problem understanding, algorithm design and endeavors such as automated algorithm selection and configuration. These techniques have largely been limited to search spaces of a single domain. In this work, we provide the means to compute exploratory landscape features for mixed-variable problems where the decision space is a mixture of continuous, binary, integer, and categorical variables. This is achieved by utilizing existing encoding techniques originating from machine learning. We provide a comprehensive juxtaposition of the results based on these different techniques. To further highlight their merit for practical applications, we design and conduct an automated algorithm selection study based on a hyperparameter optimization benchmark suite. We derive a meaningful compartmentalization of these benchmark problems by clustering based on the used landscape features. The identified clusters mimic the behavior the used algorithms exhibit. Meaning, the different clusters have different best performing algorithms. Finally, our trained algorithm selector is able to close the gap between the single best and the virtual best solver by 57.5% over all benchmark problems.

Improving Automated Algorithm Selection by Advancing Fitness Landscape Analysis

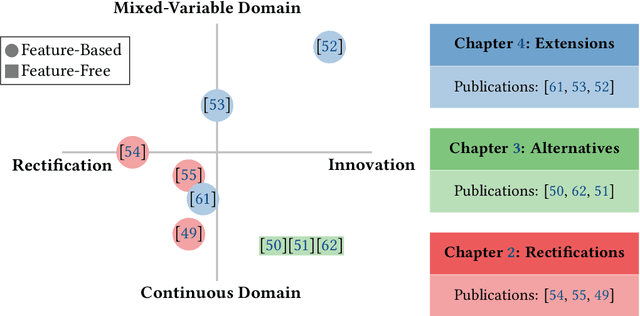
Optimization is ubiquitous in our daily lives. In the past, (sub-)optimal solutions to any problem have been derived by trial and error, sheer luck, or the expertise of knowledgeable individuals. In our contemporary age, there thankfully exists a plethora of different algorithms that can find solutions more reliably than ever before. Yet, choosing an appropriate algorithm for any given problem is challenging in itself. The field of automated algorithm selection provides various approaches to tackle this latest problem. This is done by delegating the selection of a suitable algorithm for a given problem to a complex computer model. This computer model is generated through the use of Artificial Intelligence. Many of these computer models rely on some sort of information about the problem to make a reasonable selection. Various methods exist to provide this informative input to the computer model in the form of numerical data. In this cumulative dissertation, I propose several improvements to the different variants of informative inputs. This in turn enhances and refines the current state-of-the-art of automated algorithm selection. Specifically, I identify and address current issues with the existing body of work to strengthen the foundation that future work builds upon. Furthermore, the rise of deep learning offers ample opportunities for automated algorithm selection. In several joint works, my colleagues and I developed and evaluated several different methods that replace the existing methods to extract an informative input. Lastly, automated algorithm selection approaches have been restricted to certain types of problems. I propose a method to extend the generation of informative inputs to other problem types and provide an outlook on further promising research directions.

HPO X ELA: Investigating Hyperparameter Optimization Landscapes by Means of Exploratory Landscape Analysis

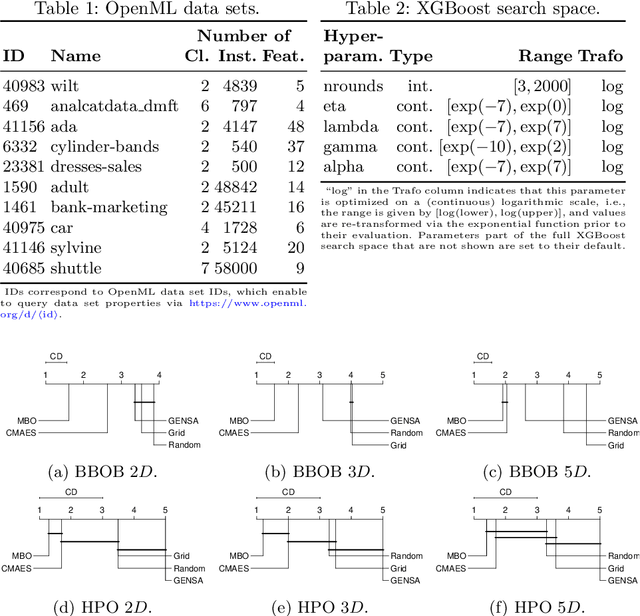
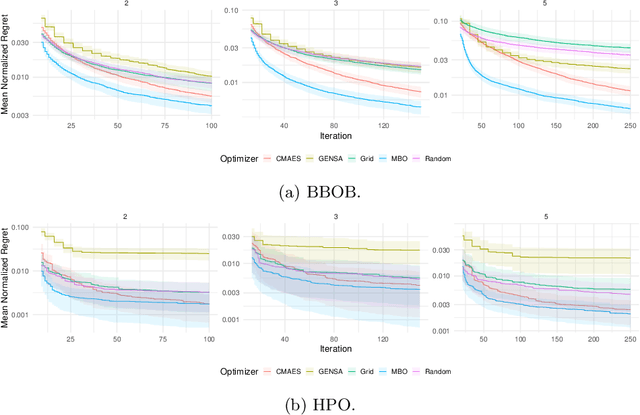
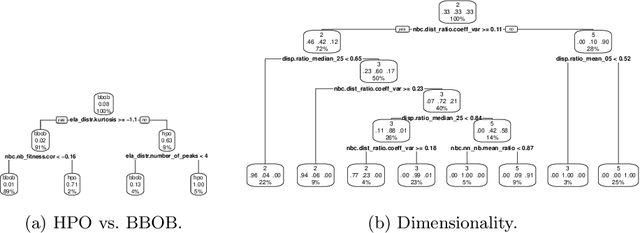
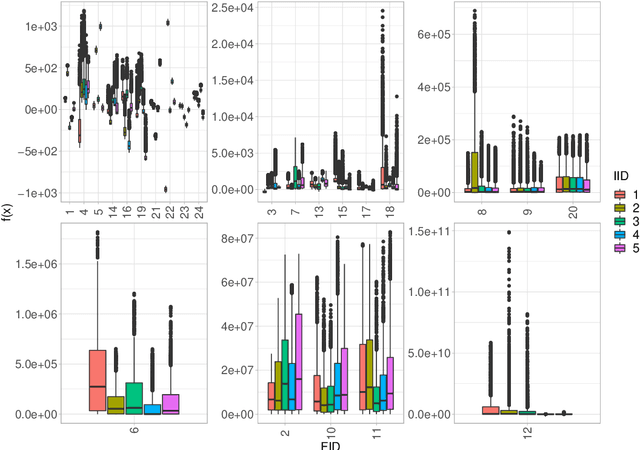
Hyperparameter optimization (HPO) is a key component of machine learning models for achieving peak predictive performance. While numerous methods and algorithms for HPO have been proposed over the last years, little progress has been made in illuminating and examining the actual structure of these black-box optimization problems. Exploratory landscape analysis (ELA) subsumes a set of techniques that can be used to gain knowledge about properties of unknown optimization problems. In this paper, we evaluate the performance of five different black-box optimizers on 30 HPO problems, which consist of two-, three- and five-dimensional continuous search spaces of the XGBoost learner trained on 10 different data sets. This is contrasted with the performance of the same optimizers evaluated on 360 problem instances from the black-box optimization benchmark (BBOB). We then compute ELA features on the HPO and BBOB problems and examine similarities and differences. A cluster analysis of the HPO and BBOB problems in ELA feature space allows us to identify how the HPO problems compare to the BBOB problems on a structural meta-level. We identify a subset of BBOB problems that are close to the HPO problems in ELA feature space and show that optimizer performance is comparably similar on these two sets of benchmark problems. We highlight open challenges of ELA for HPO and discuss potential directions of future research and applications.

A Collection of Deep Learning-based Feature-Free Approaches for Characterizing Single-Objective Continuous Fitness Landscapes

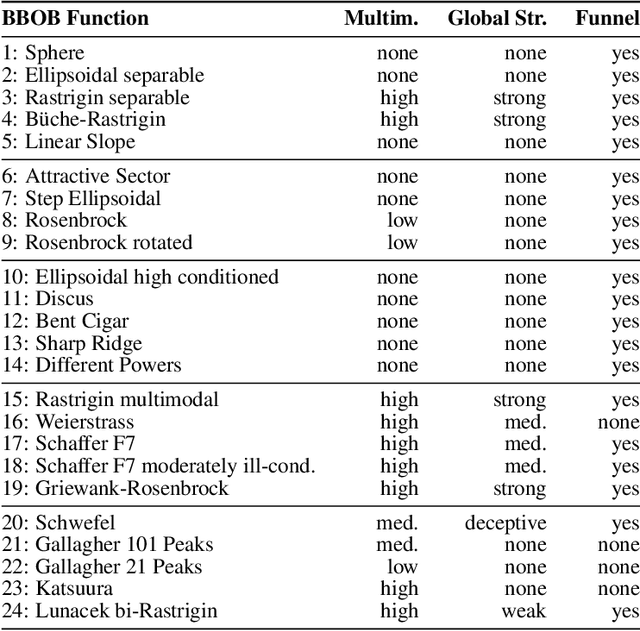
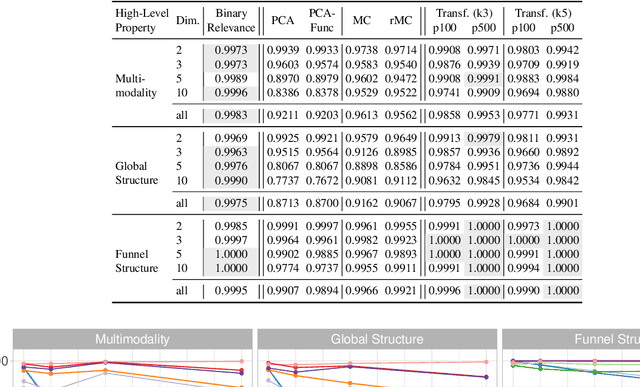
Exploratory Landscape Analysis is a powerful technique for numerically characterizing landscapes of single-objective continuous optimization problems. Landscape insights are crucial both for problem understanding as well as for assessing benchmark set diversity and composition. Despite the irrefutable usefulness of these features, they suffer from their own ailments and downsides. Hence, in this work we provide a collection of different approaches to characterize optimization landscapes. Similar to conventional landscape features, we require a small initial sample. However, instead of computing features based on that sample, we develop alternative representations of the original sample. These range from point clouds to 2D images and, therefore, are entirely feature-free. We demonstrate and validate our devised methods on the BBOB testbed and predict, with the help of Deep Learning, the high-level, expert-based landscape properties such as the degree of multimodality and the existence of funnel structures. The quality of our approaches is on par with methods relying on the traditional landscape features. Thereby, we provide an exciting new perspective on every research area which utilizes problem information such as problem understanding and algorithm design as well as automated algorithm configuration and selection.