Deep-ELA: Deep Exploratory Landscape Analysis with Self-Supervised Pretrained Transformers for Single- and Multi-Objective Continuous Optimization Problems

In many recent works, the potential of Exploratory Landscape Analysis (ELA) features to numerically characterize, in particular, single-objective continuous optimization problems has been demonstrated. These numerical features provide the input for all kinds of machine learning tasks on continuous optimization problems, ranging, i.a., from High-level Property Prediction to Automated Algorithm Selection and Automated Algorithm Configuration. Without ELA features, analyzing and understanding the characteristics of single-objective continuous optimization problems would be impossible. Yet, despite their undisputed usefulness, ELA features suffer from several drawbacks. These include, in particular, (1.) a strong correlation between multiple features, as well as (2.) its very limited applicability to multi-objective continuous optimization problems. As a remedy, recent works proposed deep learning-based approaches as alternatives to ELA. In these works, e.g., point-cloud transformers were used to characterize an optimization problem's fitness landscape. However, these approaches require a large amount of labeled training data. Within this work, we propose a hybrid approach, Deep-ELA, which combines (the benefits of) deep learning and ELA features. Specifically, we pre-trained four transformers on millions of randomly generated optimization problems to learn deep representations of the landscapes of continuous single- and multi-objective optimization problems. Our proposed framework can either be used out-of-the-box for analyzing single- and multi-objective continuous optimization problems, or subsequently fine-tuned to various tasks focussing on algorithm behavior and problem understanding.

A Collection of Deep Learning-based Feature-Free Approaches for Characterizing Single-Objective Continuous Fitness Landscapes

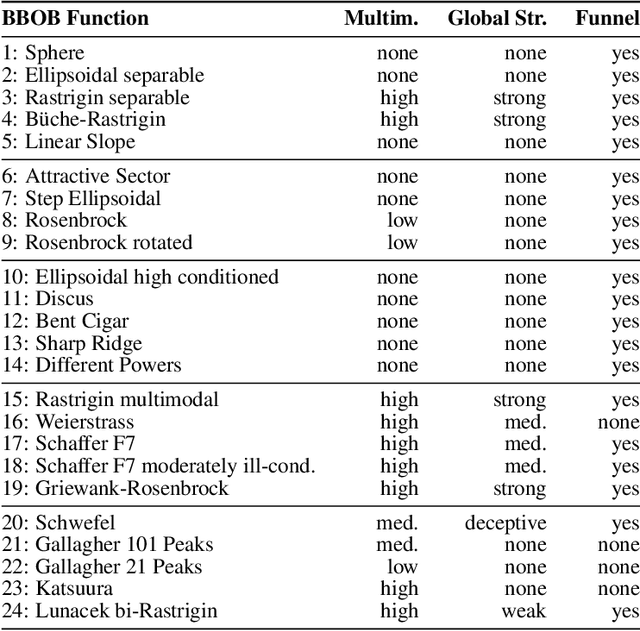
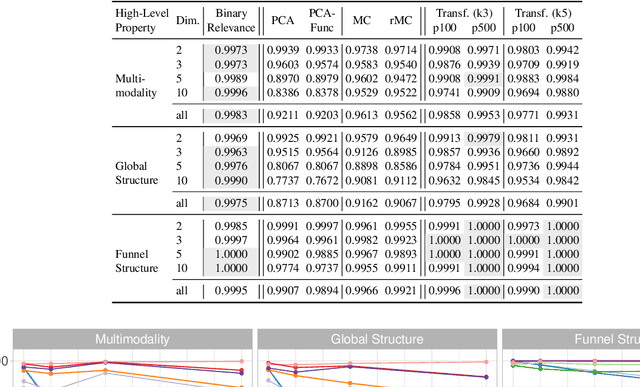
Exploratory Landscape Analysis is a powerful technique for numerically characterizing landscapes of single-objective continuous optimization problems. Landscape insights are crucial both for problem understanding as well as for assessing benchmark set diversity and composition. Despite the irrefutable usefulness of these features, they suffer from their own ailments and downsides. Hence, in this work we provide a collection of different approaches to characterize optimization landscapes. Similar to conventional landscape features, we require a small initial sample. However, instead of computing features based on that sample, we develop alternative representations of the original sample. These range from point clouds to 2D images and, therefore, are entirely feature-free. We demonstrate and validate our devised methods on the BBOB testbed and predict, with the help of Deep Learning, the high-level, expert-based landscape properties such as the degree of multimodality and the existence of funnel structures. The quality of our approaches is on par with methods relying on the traditional landscape features. Thereby, we provide an exciting new perspective on every research area which utilizes problem information such as problem understanding and algorithm design as well as automated algorithm configuration and selection.