Jacob de Nobel
From Spikes to Speech: NeuroVoc -- A Biologically Plausible Vocoder Framework for Auditory Perception and Cochlear Implant Simulation
Jun 04, 2025Abstract:We present NeuroVoc, a flexible model-agnostic vocoder framework that reconstructs acoustic waveforms from simulated neural activity patterns using an inverse Fourier transform. The system applies straightforward signal processing to neurogram representations, time-frequency binned outputs from auditory nerve fiber models. Crucially, the model architecture is modular, allowing for easy substitution or modification of the underlying auditory models. This flexibility eliminates the need for speech-coding-strategy-specific vocoder implementations when simulating auditory perception in cochlear implant (CI) users. It also allows direct comparisons between normal hearing (NH) and electrical hearing (EH) models, as demonstrated in this study. The vocoder preserves distinctive features of each model; for example, the NH model retains harmonic structure more faithfully than the EH model. We evaluated perceptual intelligibility in noise using an online Digits-in-Noise (DIN) test, where participants completed three test conditions: one with standard speech, and two with vocoded speech using the NH and EH models. Both the standard DIN test and the EH-vocoded groups were statistically equivalent to clinically reported data for NH and CI listeners. On average, the NH and EH vocoded groups increased SRT compared to the standard test by 2.4 dB and 7.1 dB, respectively. These findings show that, although some degradation occurs, the vocoder can reconstruct intelligible speech under both hearing models and accurately reflects the reduced speech-in-noise performance experienced by CI users.
Abnormal Mutations: Evolution Strategies Don't Require Gaussianity
Feb 05, 2025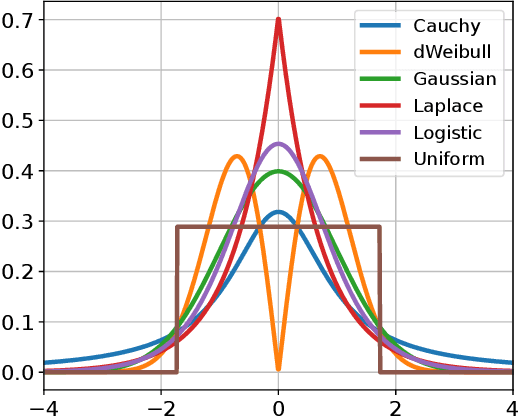

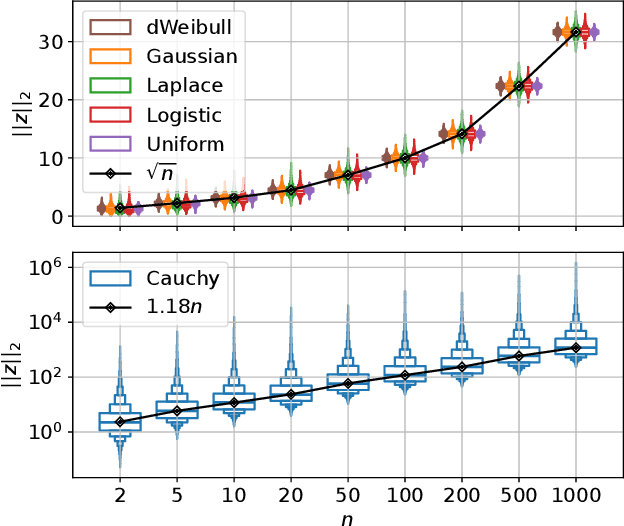

Abstract:The mutation process in evolution strategies has been interlinked with the normal distribution since its inception. Many lines of reasoning have been given for this strong dependency, ranging from maximum entropy arguments to the need for isotropy. However, some theoretical results suggest that other distributions might lead to similar local convergence properties. This paper empirically shows that a wide range of evolutionary strategies, from the (1+1)-ES to CMA-ES, show comparable optimization performance when using a mutation distribution other than the standard Gaussian. Replacing it with, e.g., uniformly distributed mutations, does not deteriorate the performance of ES, when using the default adaptation mechanism for the strategy parameters. We observe that these results hold not only for the sphere model but also for a wider range of benchmark problems.
MO-IOHinspector: Anytime Benchmarking of Multi-Objective Algorithms using IOHprofiler
Dec 10, 2024



Abstract:Benchmarking is one of the key ways in which we can gain insight into the strengths and weaknesses of optimization algorithms. In sampling-based optimization, considering the anytime behavior of an algorithm can provide valuable insights for further developments. In the context of multi-objective optimization, this anytime perspective is not as widely adopted as in the single-objective context. In this paper, we propose a new software tool which uses principles from unbounded archiving as a logging structure. This leads to a clearer separation between experimental design and subsequent analysis decisions. We integrate this approach as a new Python module into the IOHprofiler framework and demonstrate the benefits of this approach by showcasing the ability to change indicators, aggregations, and ranking procedures during the analysis pipeline.
Sampling in CMA-ES: Low Numbers of Low Discrepancy Points
Sep 24, 2024



Abstract:The Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is one of the most successful examples of a derandomized evolution strategy. However, it still relies on randomly sampling offspring, which can be done via a uniform distribution and subsequently transforming into the required Gaussian. Previous work has shown that replacing this uniform sampling with a low-discrepancy sampler, such as Halton or Sobol sequences, can improve performance over a wide set of problems. We show that iterating through small, fixed sets of low-discrepancy points can still perform better than the default uniform distribution. Moreover, using only 128 points throughout the search is sufficient to closely approximate the empirical performance of using the complete pseudorandom sequence up to dimensionality 40 on the BBOB benchmark. For lower dimensionalities (below 10), we find that using as little as 32 unique low discrepancy points performs similar or better than uniform sampling. In 2D, for which we have highly optimized low discrepancy samples available, we demonstrate that using these points yields the highest empirical performance and requires only 16 samples to improve over uniform sampling. Overall, we establish a clear relation between the $L_2$ discrepancy of the used point set and the empirical performance of the CMA-ES.
Evolving Reliable Differentiating Constraints for the Chance-constrained Maximum Coverage Problem
May 29, 2024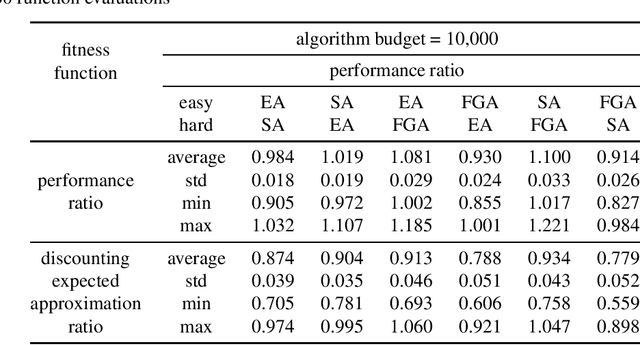
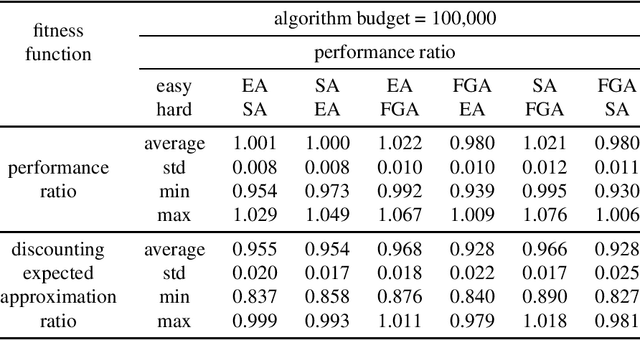
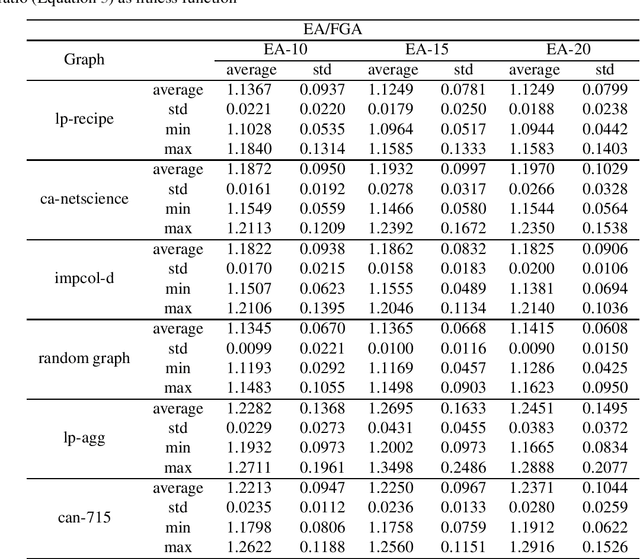
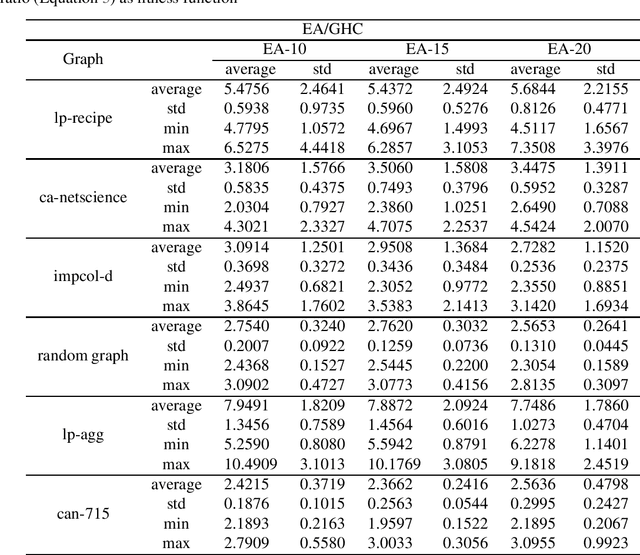
Abstract:Chance-constrained problems involve stochastic components in the constraints which can be violated with a small probability. We investigate the impact of different types of chance constraints on the performance of iterative search algorithms and study the classical maximum coverage problem in graphs with chance constraints. Our goal is to evolve reliable chance constraint settings for a given graph where the performance of algorithms differs significantly not just in expectation but with high confidence. This allows to better learn and understand how different types of algorithms can deal with different types of constraint settings and supports automatic algorithm selection. We develop an evolutionary algorithm that provides sets of chance constraints that differentiate the performance of two stochastic search algorithms with high confidence. We initially use traditional approximation ratio as the fitness function of (1+1)~EA to evolve instances, which shows inadequacy to generate reliable instances. To address this issue, we introduce a new measure to calculate the performance difference for two algorithms, which considers variances of performance ratios. Our experiments show that our approach is highly successful in solving the instability issue of the performance ratios and leads to evolving reliable sets of chance constraints with significantly different performance for various types of algorithms.
Avoiding Redundant Restarts in Multimodal Global Optimization
May 02, 2024Abstract:Na\"ive restarts of global optimization solvers when operating on multimodal search landscapes may resemble the Coupon's Collector Problem, with a potential to waste significant function evaluations budget on revisiting the same basins of attractions. In this paper, we assess the degree to which such ``duplicate restarts'' occur on standard multimodal benchmark functions, which defines the \textit{redundancy potential} of each particular landscape. We then propose a repelling mechanism to avoid such wasted restarts with the CMA-ES and investigate its efficacy on test cases with high redundancy potential compared to the standard restart mechanism.
Solving Deep Reinforcement Learning Benchmarks with Linear Policy Networks
Feb 10, 2024Abstract:Although Deep Reinforcement Learning (DRL) methods can learn effective policies for challenging problems such as Atari games and robotics tasks, algorithms are complex and training times are often long. This study investigates how evolution strategies (ES) perform compared to gradient-based deep reinforcement learning methods. We use ES to optimize the weights of a neural network via neuroevolution, performing direct policy search. We benchmark both regular networks and policy networks consisting of a single linear layer from observations to actions; for three classical ES methods and for three gradient-based methods such as PPO. Our results reveal that ES can find effective linear policies for many RL benchmark tasks, in contrast to DRL methods that can only find successful policies using much larger networks, suggesting that current benchmarks are easier to solve than previously assumed. Interestingly, also for higher complexity tasks, ES achieves results comparable to gradient-based DRL algorithms. Furthermore, we find that by directly accessing the memory state of the game, ES are able to find successful policies in Atari, outperforming DQN. While gradient-based methods have dominated the field in recent years, ES offers an alternative that is easy to implement, parallelize, understand, and tune.
Computing Star Discrepancies with Numerical Black-Box Optimization Algorithms
Jun 29, 2023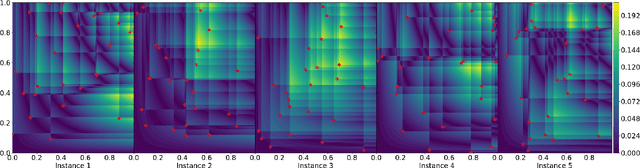
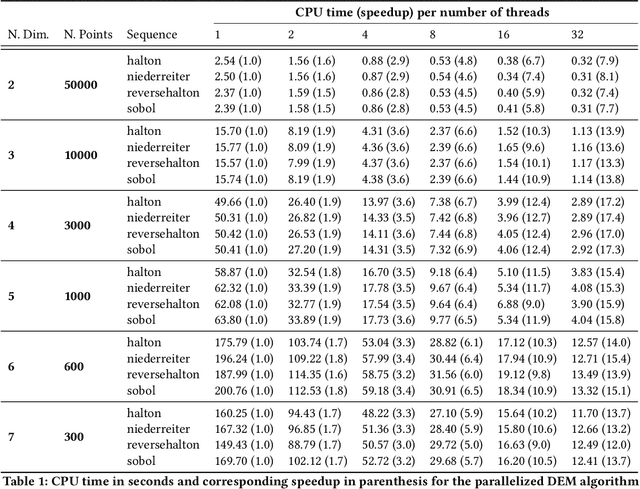
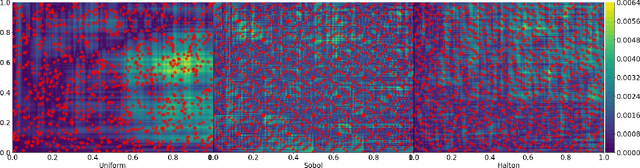
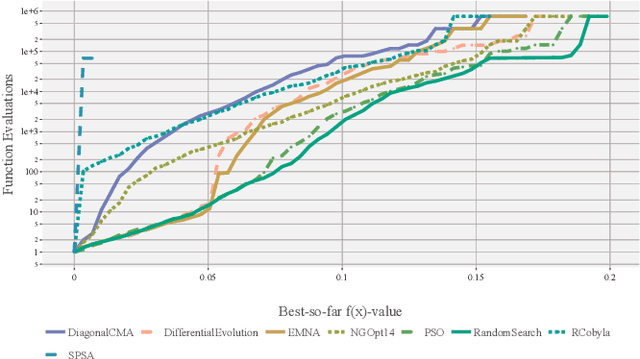
Abstract:The $L_{\infty}$ star discrepancy is a measure for the regularity of a finite set of points taken from $[0,1)^d$. Low discrepancy point sets are highly relevant for Quasi-Monte Carlo methods in numerical integration and several other applications. Unfortunately, computing the $L_{\infty}$ star discrepancy of a given point set is known to be a hard problem, with the best exact algorithms falling short for even moderate dimensions around 8. However, despite the difficulty of finding the global maximum that defines the $L_{\infty}$ star discrepancy of the set, local evaluations at selected points are inexpensive. This makes the problem tractable by black-box optimization approaches. In this work we compare 8 popular numerical black-box optimization algorithms on the $L_{\infty}$ star discrepancy computation problem, using a wide set of instances in dimensions 2 to 15. We show that all used optimizers perform very badly on a large majority of the instances and that in many cases random search outperforms even the more sophisticated solvers. We suspect that state-of-the-art numerical black-box optimization techniques fail to capture the global structure of the problem, an important shortcoming that may guide their future development. We also provide a parallel implementation of the best-known algorithm to compute the discrepancy.
When to be Discrete: Analyzing Algorithm Performance on Discretized Continuous Problems
Apr 25, 2023Abstract:The domain of an optimization problem is seen as one of its most important characteristics. In particular, the distinction between continuous and discrete optimization is rather impactful. Based on this, the optimizing algorithm, analyzing method, and more are specified. However, in practice, no problem is ever truly continuous. Whether this is caused by computing limits or more tangible properties of the problem, most variables have a finite resolution. In this work, we use the notion of the resolution of continuous variables to discretize problems from the continuous domain. We explore how the resolution impacts the performance of continuous optimization algorithms. Through a mapping to integer space, we are able to compare these continuous optimizers to discrete algorithms on the exact same problems. We show that the standard $(\mu_W, \lambda)$-CMA-ES fails when discretization is added to the problem.
What Performance Indicators to Use for Self-Adaptation in Multi-Objective Evolutionary Algorithms
Mar 08, 2023Abstract:Parameter control has succeeded in accelerating the convergence process of evolutionary algorithms. Empirical and theoretical studies for classic pseudo-Boolean problems, such as OneMax, LeadingOnes, etc., have explained the impact of parameters and helped us understand the behavior of algorithms for single-objective optimization. In this work, by transmitting the techniques of single-objective optimization, we perform an extensive experimental investigation into the behavior of the self-adaptive GSEMO variants. We test three self-adaptive mutation techniques designed for single-objective optimization for the OneMinMax, COCZ, LOTZ, and OneJumpZeroJump problems. While adopting these techniques for the GSEMO algorithm, we consider different performance metrics based on the current non-dominated solution set. These metrics are used to guide the self-adaption process. Our results indicate the benefits of self-adaptation for the tested benchmark problems. We reveal that the choice of metrics significantly affects the performance of the self-adaptive algorithms. The self-adaptation methods based on the progress in one objective can perform better than the methods using multi-objective metrics such as hypervolume, inverted generational distance, and the number of the obtained Pareto solutions. Moreover, we find that the self-adaptive methods benefit from the large population size for OneMinMax and COCZ.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge