Luís Paquete
University of Coimbra, Portugal
Computing Star Discrepancies with Numerical Black-Box Optimization Algorithms
Jun 29, 2023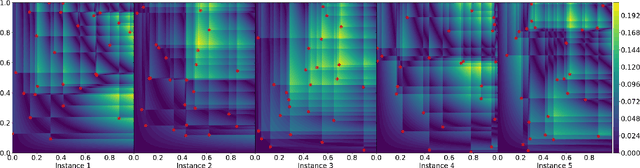
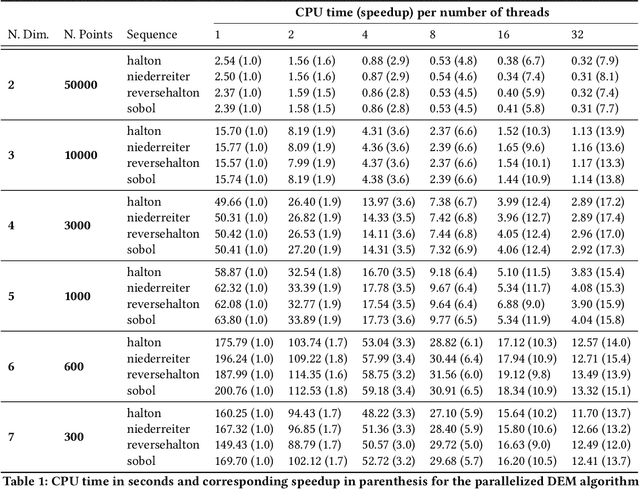
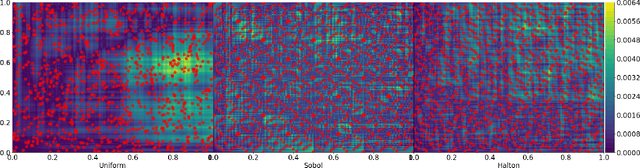
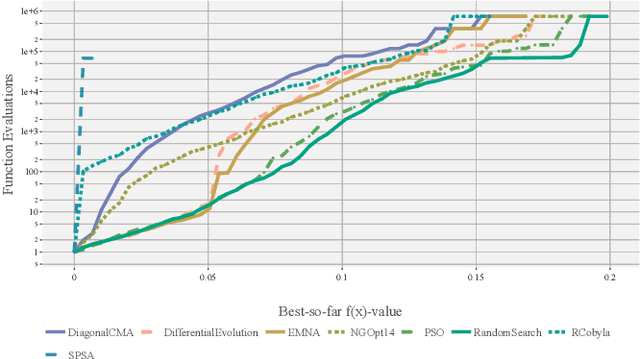
Abstract:The $L_{\infty}$ star discrepancy is a measure for the regularity of a finite set of points taken from $[0,1)^d$. Low discrepancy point sets are highly relevant for Quasi-Monte Carlo methods in numerical integration and several other applications. Unfortunately, computing the $L_{\infty}$ star discrepancy of a given point set is known to be a hard problem, with the best exact algorithms falling short for even moderate dimensions around 8. However, despite the difficulty of finding the global maximum that defines the $L_{\infty}$ star discrepancy of the set, local evaluations at selected points are inexpensive. This makes the problem tractable by black-box optimization approaches. In this work we compare 8 popular numerical black-box optimization algorithms on the $L_{\infty}$ star discrepancy computation problem, using a wide set of instances in dimensions 2 to 15. We show that all used optimizers perform very badly on a large majority of the instances and that in many cases random search outperforms even the more sophisticated solvers. We suspect that state-of-the-art numerical black-box optimization techniques fail to capture the global structure of the problem, an important shortcoming that may guide their future development. We also provide a parallel implementation of the best-known algorithm to compute the discrepancy.
Reproducibility in Evolutionary Computation
Feb 05, 2021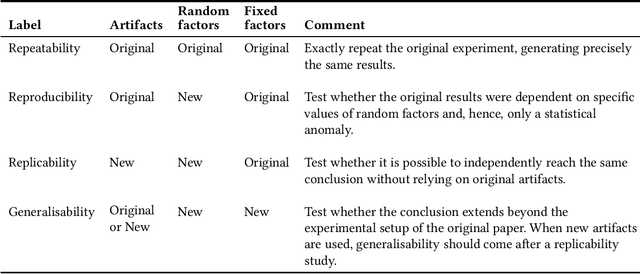
Abstract:Experimental studies are prevalent in Evolutionary Computation (EC), and concerns about the reproducibility and replicability of such studies have increased in recent times, reflecting similar concerns in other scientific fields. In this article, we suggest a classification of different types of reproducibility that refines the badge system of the Association of Computing Machinery (ACM) adopted by TELO. We discuss, within the context of EC, the different types of reproducibility as well as the concepts of artifact and measurement, which are crucial for claiming reproducibility. We identify cultural and technical obstacles to reproducibility in the EC field. Finally, we provide guidelines and suggest tools that may help to overcome some of these reproducibility obstacles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge