Annealed Entropic Allocation for Ranking and Selection

We propose Annealed Entropic Allocation, an annealed weighted soft-min framework for sequential budget allocation in ranking and selection. The central idea is to replace the non-smooth maximin large-deviation rate objective with a weighted log-sum-exp surrogate that aggregates challenger-specific pairwise scores through soft-min weights, mitigating hard switching when several challengers are nearly active. To improve finite-budget discrimination, we incorporate the saddlepoint approximation -- a sub-exponential correction derived from refined pairwise tail asymptotics. Because these corrections are sub-exponential and the smoothing parameter is annealed to zero, the surrogate preserves the same first-order large-deviation target as the classical maximin formulation. We show that the surrogate converges uniformly to the hard minimum, that the soft-min weights concentrate on the active challengers, and that, under fixed weights, the induced target allocation map is continuous on the simplex interior. Numerical experiments on Gaussian and exponential instances demonstrate competitive performance, especially when multiple challengers are nearly tied.

Maximizing Reliability with Bayesian Optimization

Bayesian optimization (BO) is a popular, sample-efficient technique for expensive, black-box optimization. One such problem arising in manufacturing is that of maximizing the reliability, or equivalently minimizing the probability of a failure, of a design which is subject to random perturbations - a problem that can involve extremely rare failures ($P_\mathrm{fail} = 10^{-6}-10^{-8}$). In this work, we propose two BO methods based on Thompson sampling and knowledge gradient, the latter approximating the one-step Bayes-optimal policy for minimizing the logarithm of the failure probability. Both methods incorporate importance sampling to target extremely small failure probabilities. Empirical results show the proposed methods outperform existing methods in both extreme and non-extreme regimes.

Bayesian Optimisation: Which Constraints Matter?

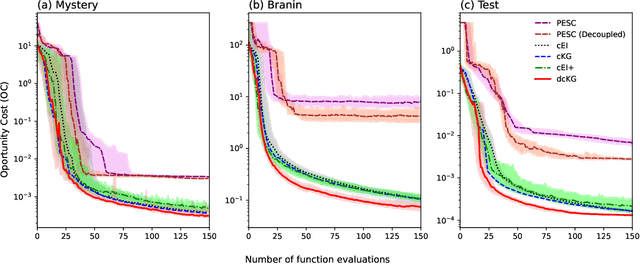
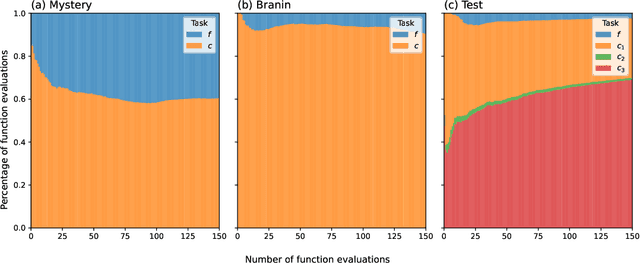
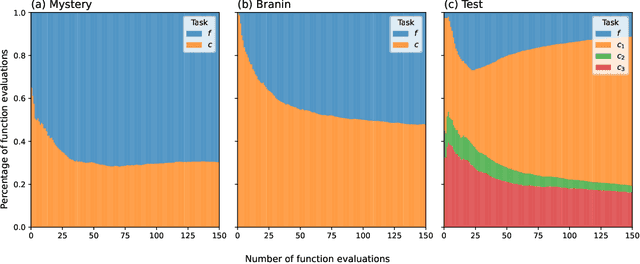
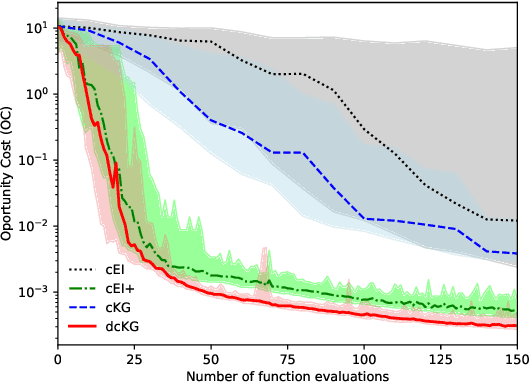
Bayesian optimisation has proven to be a powerful tool for expensive global black-box optimisation problems. In this paper, we propose new Bayesian optimisation variants of the popular Knowledge Gradient acquisition functions for problems with \emph{decoupled} black-box constraints, in which subsets of the objective and constraint functions may be evaluated independently. In particular, our methods aim to take into account that often only a handful of the constraints may be binding at the optimum, and hence we should evaluate only relevant constraints when trying to optimise a function. We empirically benchmark these methods against existing methods and demonstrate their superiority over the state-of-the-art.

Learning in Repeated Multi-Objective Stackelberg Games with Payoff Manipulation

We study payoff manipulation in repeated multi-objective Stackelberg games, where a leader may strategically influence a follower's deterministic best response, e.g., by offering a share of their own payoff. We assume that the follower's utility function, representing preferences over multiple objectives, is unknown but linear, and its weight parameter must be inferred through interaction. This introduces a sequential decision-making challenge for the leader, who must balance preference elicitation with immediate utility maximisation. We formalise this problem and propose manipulation policies based on expected utility (EU) and long-term expected utility (longEU), which guide the leader in selecting actions and offering incentives that trade off short-term gains with long-term impact. We prove that under infinite repeated interactions, longEU converges to the optimal manipulation. Empirical results across benchmark environments demonstrate that our approach improves cumulative leader utility while promoting mutually beneficial outcomes, all without requiring explicit negotiation or prior knowledge of the follower's utility function.

Bayesian Optimization with Preference Exploration by Monotonic Neural Network Ensemble

Many real-world black-box optimization problems have multiple conflicting objectives. Rather than attempting to approximate the entire set of Pareto-optimal solutions, interactive preference learning allows to focus the search on the most relevant subset. However, few previous studies have exploited the fact that utility functions are usually monotonic. In this paper, we address the Bayesian Optimization with Preference Exploration (BOPE) problem and propose using a neural network ensemble as a utility surrogate model. This approach naturally integrates monotonicity and supports pairwise comparison data. Our experiments demonstrate that the proposed method outperforms state-of-the-art approaches and exhibits robustness to noise in utility evaluations. An ablation study highlights the critical role of monotonicity in enhancing performance.

Bayesian Optimization of Bilevel Problems

Bilevel optimization, a hierarchical mathematical framework where one optimization problem is nested within another, has emerged as a powerful tool for modeling complex decision-making processes in various fields such as economics, engineering, and machine learning. This paper focuses on bilevel optimization where both upper-level and lower-level functions are black boxes and expensive to evaluate. We propose a Bayesian Optimization framework that models the upper and lower-level functions as Gaussian processes over the combined space of upper and lower-level decisions, allowing us to exploit knowledge transfer between different sub-problems. Additionally, we propose a novel acquisition function for this model. Our experimental results demonstrate that the proposed algorithm is highly sample-efficient and outperforms existing methods in finding high-quality solutions.

Respecting the limit:Bayesian optimization with a bound on the optimal value

In many real-world optimization problems, we have prior information about what objective function values are achievable. In this paper, we study the scenario that we have either exact knowledge of the minimum value or a, possibly inexact, lower bound on its value. We propose bound-aware Bayesian optimization (BABO), a Bayesian optimization method that uses a new surrogate model and acquisition function to utilize such prior information. We present SlogGP, a new surrogate model that incorporates bound information and adapts the Expected Improvement (EI) acquisition function accordingly. Empirical results on a variety of benchmarks demonstrate the benefit of taking prior information about the optimal value into account, and that the proposed approach significantly outperforms existing techniques. Furthermore, we notice that even in the absence of prior information on the bound, the proposed SlogGP surrogate model still performs better than the standard GP model in most cases, which we explain by its larger expressiveness.

Bayesian Optimization for Non-Convex Two-Stage Stochastic Optimization Problems

Bayesian optimization is a sample-efficient method for solving expensive, black-box optimization problems. Stochastic programming concerns optimization under uncertainty where, typically, average performance is the quantity of interest. In the first stage of a two-stage problem, here-and-now decisions must be made in the face of this uncertainty, while in the second stage, wait-and-see decisions are made after the uncertainty has been resolved. Many methods in stochastic programming assume that the objective is cheap to evaluate and linear or convex. In this work, we apply Bayesian optimization to solve non-convex, two-stage stochastic programs which are expensive to evaluate. We formulate a knowledge-gradient-based acquisition function to jointly optimize the first- and second-stage variables, establish a guarantee of asymptotic consistency and provide a computationally efficient approximation. We demonstrate comparable empirical results to an alternative we formulate which alternates its focus between the two variable types, and superior empirical results over the standard, naive, two-step benchmark. We show that differences in the dimension and length scales between the variable types can lead to inefficiencies of the two-step algorithm, while the joint and alternating acquisition functions perform well in all problems tested. Experiments are conducted on both synthetic and real-world examples.

Identifying the Best Arm in the Presence of Global Environment Shifts

This paper formulates a new Best-Arm Identification problem in the non-stationary stochastic bandits setting, where the means of all arms are shifted in the same way due to a global influence of the environment. The aim is to identify the unique best arm across environmental change given a fixed total budget. While this setting can be regarded as a special case of Adversarial Bandits or Corrupted Bandits, we demonstrate that existing solutions tailored to those settings do not fully utilise the nature of this global influence, and thus, do not work well in practice (despite their theoretical guarantees). To overcome this issue, in this paper we develop a novel selection policy that is consistent and robust in dealing with global environmental shifts. We then propose an allocation policy, LinLUCB, which exploits information about global shifts across all arms in each environment. Empirical tests depict a significant improvement in our policies against other existing methods.

Clustering in Dynamic Environments: A Framework for Benchmark Dataset Generation With Heterogeneous Changes

Clustering in dynamic environments is of increasing importance, with broad applications ranging from real-time data analysis and online unsupervised learning to dynamic facility location problems. While meta-heuristics have shown promising effectiveness in static clustering tasks, their application for tracking optimal clustering solutions or robust clustering over time in dynamic environments remains largely underexplored. This is partly due to a lack of dynamic datasets with diverse, controllable, and realistic dynamic characteristics, hindering systematic performance evaluations of clustering algorithms in various dynamic scenarios. This deficiency leads to a gap in our understanding and capability to effectively design algorithms for clustering in dynamic environments. To bridge this gap, this paper introduces the Dynamic Dataset Generator (DDG). DDG features multiple dynamic Gaussian components integrated with a range of heterogeneous, local, and global changes. These changes vary in spatial and temporal severity, patterns, and domain of influence, providing a comprehensive tool for simulating a wide range of dynamic scenarios.