Clustering in Dynamic Environments: A Framework for Benchmark Dataset Generation With Heterogeneous Changes

Clustering in dynamic environments is of increasing importance, with broad applications ranging from real-time data analysis and online unsupervised learning to dynamic facility location problems. While meta-heuristics have shown promising effectiveness in static clustering tasks, their application for tracking optimal clustering solutions or robust clustering over time in dynamic environments remains largely underexplored. This is partly due to a lack of dynamic datasets with diverse, controllable, and realistic dynamic characteristics, hindering systematic performance evaluations of clustering algorithms in various dynamic scenarios. This deficiency leads to a gap in our understanding and capability to effectively design algorithms for clustering in dynamic environments. To bridge this gap, this paper introduces the Dynamic Dataset Generator (DDG). DDG features multiple dynamic Gaussian components integrated with a range of heterogeneous, local, and global changes. These changes vary in spatial and temporal severity, patterns, and domain of influence, providing a comprehensive tool for simulating a wide range of dynamic scenarios.

GNBG: A Generalized and Configurable Benchmark Generator for Continuous Numerical Optimization

As optimization challenges continue to evolve, so too must our tools and understanding. To effectively assess, validate, and compare optimization algorithms, it is crucial to use a benchmark test suite that encompasses a diverse range of problem instances with various characteristics. Traditional benchmark suites often consist of numerous fixed test functions, making it challenging to align these with specific research objectives, such as the systematic evaluation of algorithms under controllable conditions. This paper introduces the Generalized Numerical Benchmark Generator (GNBG) for single-objective, box-constrained, continuous numerical optimization. Unlike existing approaches that rely on multiple baseline functions and transformations, GNBG utilizes a single, parametric, and configurable baseline function. This design allows for control over various problem characteristics. Researchers using GNBG can generate instances that cover a broad array of morphological features, from unimodal to highly multimodal functions, various local optima patterns, and symmetric to highly asymmetric structures. The generated problems can also vary in separability, variable interaction structures, dimensionality, conditioning, and basin shapes. These customizable features enable the systematic evaluation and comparison of optimization algorithms, allowing researchers to probe their strengths and weaknesses under diverse and controllable conditions.

GNBG-Generated Test Suite for Box-Constrained Numerical Global Optimization

This document introduces a set of 24 box-constrained numerical global optimization problem instances, systematically constructed using the Generalized Numerical Benchmark Generator (GNBG). These instances cover a broad spectrum of problem features, including varying degrees of modality, ruggedness, symmetry, conditioning, variable interaction structures, basin linearity, and deceptiveness. Purposefully designed, this test suite offers varying difficulty levels and problem characteristics, facilitating rigorous evaluation and comparative analysis of optimization algorithms. By presenting these problems, we aim to provide researchers with a structured platform to assess the strengths and weaknesses of their algorithms against challenges with known, controlled characteristics. For reproducibility, the MATLAB source code for this test suite is publicly available.

Variable Functioning and Its Application to Large Scale Steel Frame Design Optimization

To solve complex real-world problems, heuristics and concept-based approaches can be used in order to incorporate information into the problem. In this study, a concept-based approach called variable functioning Fx is introduced to reduce the optimization variables and narrow down the search space. In this method, the relationships among one or more subset of variables are defined with functions using information prior to optimization; thus, instead of modifying the variables in the search process, the function variables are optimized. By using problem structure analysis technique and engineering expert knowledge, the $Fx$ method is used to enhance the steel frame design optimization process as a complex real-world problem. The proposed approach is coupled with particle swarm optimization and differential evolution algorithms and used for three case studies. The algorithms are applied to optimize the case studies by considering the relationships among column cross-section areas. The results show that $Fx$ can significantly improve both the convergence rate and the final design of a frame structure, even if it is only used for seeding.

Generating Large-scale Dynamic Optimization Problem Instances Using the Generalized Moving Peaks Benchmark

This document describes the generalized moving peaks benchmark (GMPB) and how it can be used to generate problem instances for continuous large-scale dynamic optimization problems. It presents a set of 15 benchmark problems, the relevant source code, and a performance indicator, designed for comparative studies and competitions in large-scale dynamic optimization. Although its primary purpose is to provide a coherent basis for running competitions, its generality allows the interested reader to use this document as a guide to design customized problem instances to investigate issues beyond the scope of the presented benchmark suite. To this end, we explain the modular structure of the GMPB and how its constituents can be assembled to form problem instances with a variety of controllable characteristics ranging from unimodal to highly multimodal, symmetric to highly asymmetric, smooth to highly irregular, and various degrees of variable interaction and ill-conditioning.

Generalized Moving Peaks Benchmark

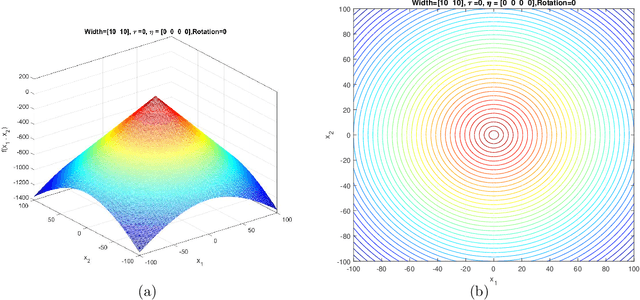
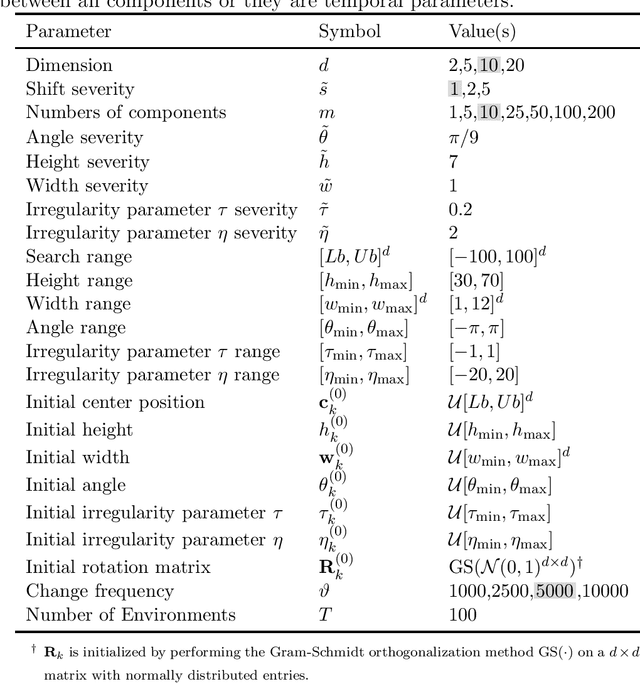
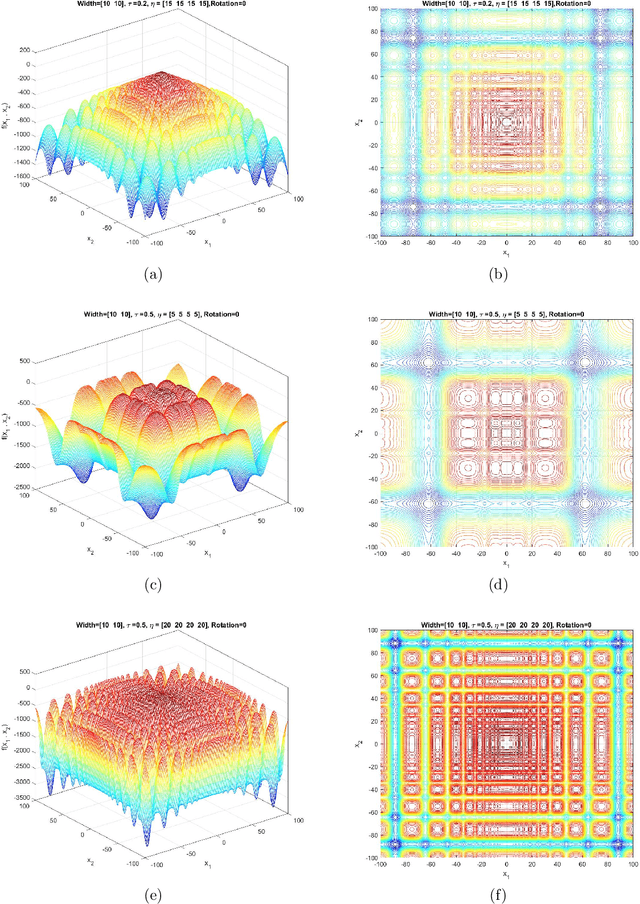
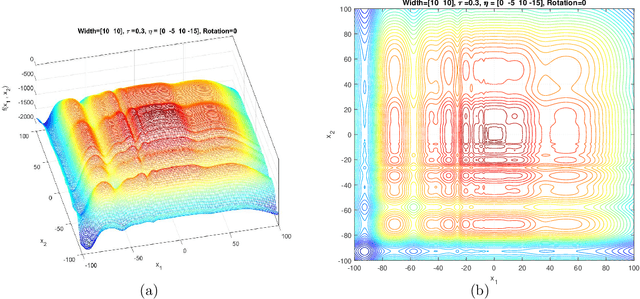
This document describes the Generalized Moving Peaks Benchmark (GMPB) that generates continuous dynamic optimization problem instances. The landscapes generated by GMPB are constructed by assembling several components with a variety of controllable characteristics ranging from unimodal to highly multimodal, symmetric to highly asymmetric, smooth to highly irregular, and various degrees of variable interaction and ill-conditioning. In this document, we explain how these characteristics can be generated by different parameter settings of GMPB. The MATLAB source code of GMPB is also explained. This document forms the basis for a range of competitions on Evolutionary Continuous Dynamic Optimization in the upcoming well-known conferences.