Clustering in Dynamic Environments: A Framework for Benchmark Dataset Generation With Heterogeneous Changes

Clustering in dynamic environments is of increasing importance, with broad applications ranging from real-time data analysis and online unsupervised learning to dynamic facility location problems. While meta-heuristics have shown promising effectiveness in static clustering tasks, their application for tracking optimal clustering solutions or robust clustering over time in dynamic environments remains largely underexplored. This is partly due to a lack of dynamic datasets with diverse, controllable, and realistic dynamic characteristics, hindering systematic performance evaluations of clustering algorithms in various dynamic scenarios. This deficiency leads to a gap in our understanding and capability to effectively design algorithms for clustering in dynamic environments. To bridge this gap, this paper introduces the Dynamic Dataset Generator (DDG). DDG features multiple dynamic Gaussian components integrated with a range of heterogeneous, local, and global changes. These changes vary in spatial and temporal severity, patterns, and domain of influence, providing a comprehensive tool for simulating a wide range of dynamic scenarios.

Semantic-Preserving Feature Partitioning for Multi-View Ensemble Learning

In machine learning, the exponential growth of data and the associated ``curse of dimensionality'' pose significant challenges, particularly with expansive yet sparse datasets. Addressing these challenges, multi-view ensemble learning (MEL) has emerged as a transformative approach, with feature partitioning (FP) playing a pivotal role in constructing artificial views for MEL. Our study introduces the Semantic-Preserving Feature Partitioning (SPFP) algorithm, a novel method grounded in information theory. The SPFP algorithm effectively partitions datasets into multiple semantically consistent views, enhancing the MEL process. Through extensive experiments on eight real-world datasets, ranging from high-dimensional with limited instances to low-dimensional with high instances, our method demonstrates notable efficacy. It maintains model accuracy while significantly improving uncertainty measures in scenarios where high generalization performance is achievable. Conversely, it retains uncertainty metrics while enhancing accuracy where high generalization accuracy is less attainable. An effect size analysis further reveals that the SPFP algorithm outperforms benchmark models by large effect size and reduces computational demands through effective dimensionality reduction. The substantial effect sizes observed in most experiments underscore the algorithm's significant improvements in model performance.

GNBG: A Generalized and Configurable Benchmark Generator for Continuous Numerical Optimization

As optimization challenges continue to evolve, so too must our tools and understanding. To effectively assess, validate, and compare optimization algorithms, it is crucial to use a benchmark test suite that encompasses a diverse range of problem instances with various characteristics. Traditional benchmark suites often consist of numerous fixed test functions, making it challenging to align these with specific research objectives, such as the systematic evaluation of algorithms under controllable conditions. This paper introduces the Generalized Numerical Benchmark Generator (GNBG) for single-objective, box-constrained, continuous numerical optimization. Unlike existing approaches that rely on multiple baseline functions and transformations, GNBG utilizes a single, parametric, and configurable baseline function. This design allows for control over various problem characteristics. Researchers using GNBG can generate instances that cover a broad array of morphological features, from unimodal to highly multimodal functions, various local optima patterns, and symmetric to highly asymmetric structures. The generated problems can also vary in separability, variable interaction structures, dimensionality, conditioning, and basin shapes. These customizable features enable the systematic evaluation and comparison of optimization algorithms, allowing researchers to probe their strengths and weaknesses under diverse and controllable conditions.

GNBG-Generated Test Suite for Box-Constrained Numerical Global Optimization

This document introduces a set of 24 box-constrained numerical global optimization problem instances, systematically constructed using the Generalized Numerical Benchmark Generator (GNBG). These instances cover a broad spectrum of problem features, including varying degrees of modality, ruggedness, symmetry, conditioning, variable interaction structures, basin linearity, and deceptiveness. Purposefully designed, this test suite offers varying difficulty levels and problem characteristics, facilitating rigorous evaluation and comparative analysis of optimization algorithms. By presenting these problems, we aim to provide researchers with a structured platform to assess the strengths and weaknesses of their algorithms against challenges with known, controlled characteristics. For reproducibility, the MATLAB source code for this test suite is publicly available.

Evolutionary Dynamic Optimization Laboratory: A MATLAB Optimization Platform for Education and Experimentation in Dynamic Environments

Many real-world optimization problems possess dynamic characteristics. Evolutionary dynamic optimization algorithms (EDOAs) aim to tackle the challenges associated with dynamic optimization problems. Looking at the existing works, the results reported for a given EDOA can sometimes be considerably different. This issue occurs because the source codes of many EDOAs, which are usually very complex algorithms, have not been made publicly available. Indeed, the complexity of components and mechanisms used in many EDOAs makes their re-implementation error-prone. In this paper, to assist researchers in performing experiments and comparing their algorithms against several EDOAs, we develop an open-source MATLAB platform for EDOAs, called Evolutionary Dynamic Optimization LABoratory (EDOLAB). This platform also contains an education module that can be used for educational purposes. In the education module, the user can observe a) a 2-dimensional problem space and how its morphology changes after each environmental change, b) the behaviors of individuals over time, and c) how the EDOA reacts to environmental changes and tries to track the moving optimum. In addition to being useful for research and education purposes, EDOLAB can also be used by practitioners to solve their real-world problems. The current version of EDOLAB includes 25 EDOAs and three fully-parametric benchmark generators. The MATLAB source code for EDOLAB is publicly available and can be accessed from [https://github.com/EDOLAB-platform/EDOLAB-MATLAB].

Generating Large-scale Dynamic Optimization Problem Instances Using the Generalized Moving Peaks Benchmark

This document describes the generalized moving peaks benchmark (GMPB) and how it can be used to generate problem instances for continuous large-scale dynamic optimization problems. It presents a set of 15 benchmark problems, the relevant source code, and a performance indicator, designed for comparative studies and competitions in large-scale dynamic optimization. Although its primary purpose is to provide a coherent basis for running competitions, its generality allows the interested reader to use this document as a guide to design customized problem instances to investigate issues beyond the scope of the presented benchmark suite. To this end, we explain the modular structure of the GMPB and how its constituents can be assembled to form problem instances with a variety of controllable characteristics ranging from unimodal to highly multimodal, symmetric to highly asymmetric, smooth to highly irregular, and various degrees of variable interaction and ill-conditioning.

Generalized Moving Peaks Benchmark

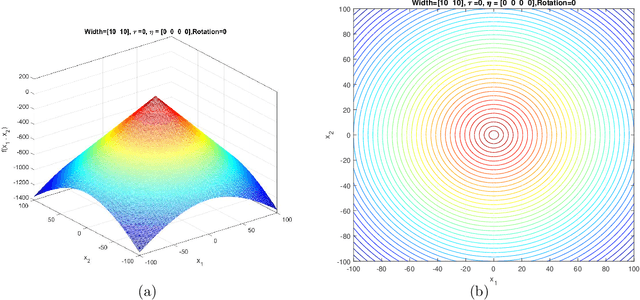
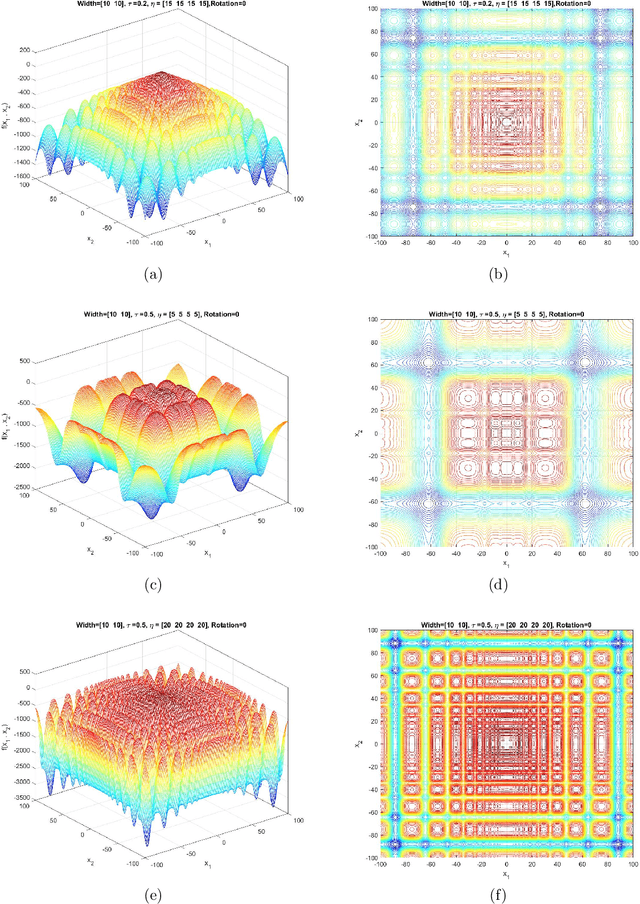
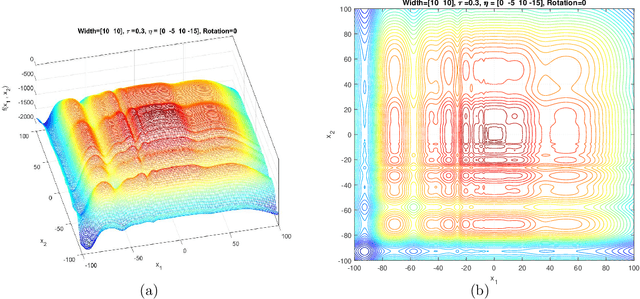
This document describes the Generalized Moving Peaks Benchmark (GMPB) that generates continuous dynamic optimization problem instances. The landscapes generated by GMPB are constructed by assembling several components with a variety of controllable characteristics ranging from unimodal to highly multimodal, symmetric to highly asymmetric, smooth to highly irregular, and various degrees of variable interaction and ill-conditioning. In this document, we explain how these characteristics can be generated by different parameter settings of GMPB. The MATLAB source code of GMPB is also explained. This document forms the basis for a range of competitions on Evolutionary Continuous Dynamic Optimization in the upcoming well-known conferences.

A Review of the Family of Artificial Fish Swarm Algorithms: Recent Advances and Applications

The Artificial Fish Swarm Algorithm (AFSA) is inspired by the ecological behaviors of fish schooling in nature, viz., the preying, swarming, following and random behaviors. Owing to a number of salient properties, which include flexibility, fast convergence, and insensitivity to the initial parameter settings, the family of AFSA has emerged as an effective Swarm Intelligence (SI) methodology that has been widely applied to solve real-world optimization problems. Since its introduction in 2002, many improved and hybrid AFSA models have been developed to tackle continuous, binary, and combinatorial optimization problems. This paper aims to present a concise review of the family of AFSA, encompassing the original ASFA and its improvements, continuous, binary, discrete, and hybrid models, as well as the associated applications. A comprehensive survey on the AFSA from its introduction to 2012 can be found in [1]. As such, we focus on a total of {\color{blue}123} articles published in high-quality journals since 2013. We also discuss possible AFSA enhancements and highlight future research directions for the family of AFSA-based models.