Zeneng She
Evolutionary Dynamic Optimization Laboratory: A MATLAB Optimization Platform for Education and Experimentation in Dynamic Environments
Aug 24, 2023



Abstract:Many real-world optimization problems possess dynamic characteristics. Evolutionary dynamic optimization algorithms (EDOAs) aim to tackle the challenges associated with dynamic optimization problems. Looking at the existing works, the results reported for a given EDOA can sometimes be considerably different. This issue occurs because the source codes of many EDOAs, which are usually very complex algorithms, have not been made publicly available. Indeed, the complexity of components and mechanisms used in many EDOAs makes their re-implementation error-prone. In this paper, to assist researchers in performing experiments and comparing their algorithms against several EDOAs, we develop an open-source MATLAB platform for EDOAs, called Evolutionary Dynamic Optimization LABoratory (EDOLAB). This platform also contains an education module that can be used for educational purposes. In the education module, the user can observe a) a 2-dimensional problem space and how its morphology changes after each environmental change, b) the behaviors of individuals over time, and c) how the EDOA reacts to environmental changes and tries to track the moving optimum. In addition to being useful for research and education purposes, EDOLAB can also be used by practitioners to solve their real-world problems. The current version of EDOLAB includes 25 EDOAs and three fully-parametric benchmark generators. The MATLAB source code for EDOLAB is publicly available and can be accessed from [https://github.com/EDOLAB-platform/EDOLAB-MATLAB].
Evolutionary Multiparty Distance Minimization
Jul 27, 2022
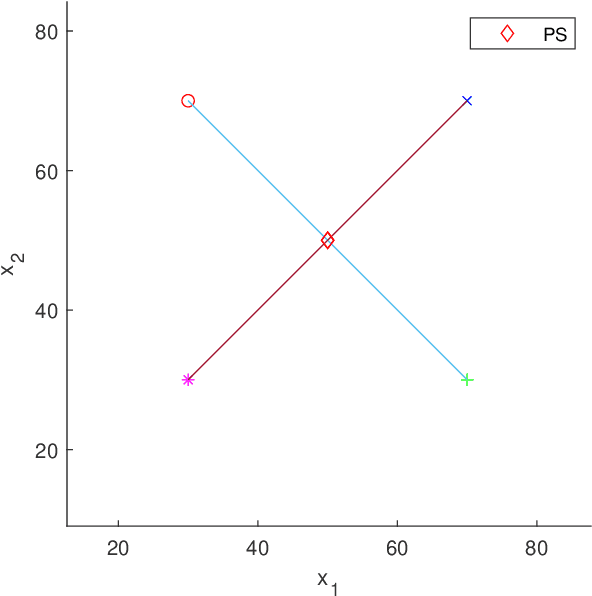
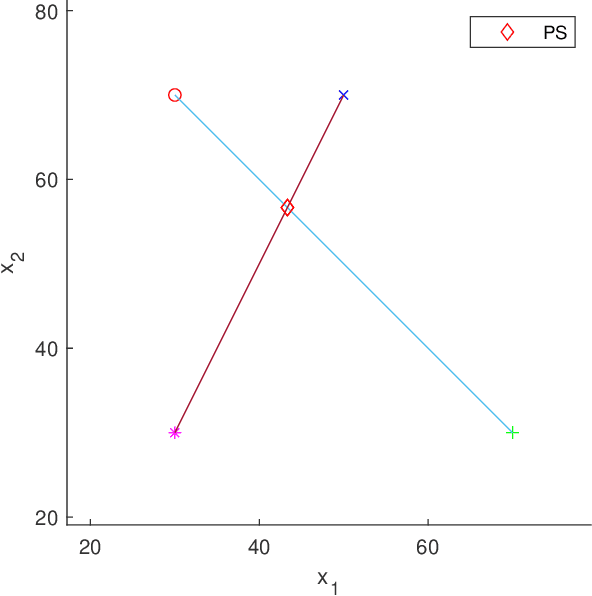
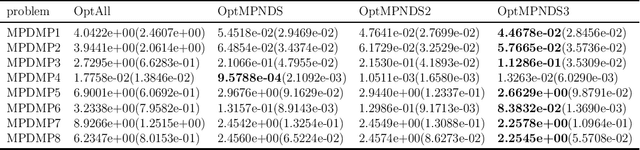
Abstract:In the field of evolutionary multiobjective optimization, the decision maker (DM) concerns conflicting objectives. In the real-world applications, there usually exist more than one DM and each DM concerns parts of these objectives. Multiparty multiobjective optimization problems (MPMOPs) are proposed to depict the MOP with multiple decision makers involved, where each party concerns about certain some objectives of all. However, in the evolutionary computation field, there is not much attention paid on MPMOPs. This paper constructs a series of MPMOPs based on distance minimization problems (DMPs), whose Pareto optimal solutions can be vividly visualized. To address MPMOPs, the new proposed algorithm OptMPNDS3 uses the multiparty initializing method to initialize the population and takes JADE2 operator to generate the offsprings. OptMPNDS3 is compared with OptAll, OptMPNDS and OptMPNDS2 on the problem suite. The result shows that OptMPNDS3 is strongly comparable to other algorithms
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge