Data-Efficient Interactive Multi-Objective Optimization Using ParEGO

Multi-objective optimization is a widely studied problem in diverse fields, such as engineering and finance, that seeks to identify a set of non-dominated solutions that provide optimal trade-offs among competing objectives. However, the computation of the entire Pareto front can become prohibitively expensive, both in terms of computational resources and time, particularly when dealing with a large number of objectives. In practical applications, decision-makers (DMs) will select a single solution of the Pareto front that aligns with their preferences to be implemented; thus, traditional multi-objective algorithms invest a lot of budget sampling solutions that are not interesting for the DM. In this paper, we propose two novel algorithms that employ Gaussian Processes and advanced discretization methods to efficiently locate the most preferred region of the Pareto front in expensive-to-evaluate problems. Our approach involves interacting with the decision-maker to guide the optimization process towards their preferred trade-offs. Our experimental results demonstrate that our proposed algorithms are effective in finding non-dominated solutions that align with the decision-maker's preferences while maintaining computational efficiency.

Bayesian Optimization of Multiple Objectives with Different Latencies

Multi-objective Bayesian optimization aims to find the Pareto front of optimal trade-offs between a set of expensive objectives while collecting as few samples as possible. In some cases, it is possible to evaluate the objectives separately, and a different latency or evaluation cost can be associated with each objective. This presents an opportunity to learn the Pareto front faster by evaluating the cheaper objectives more frequently. We propose a scalarization based knowledge gradient acquisition function which accounts for the different evaluation costs of the objectives. We prove consistency of the algorithm and show empirically that it significantly outperforms a benchmark algorithm which always evaluates both objectives.

Multiobjective Ranking and Selection Using Stochastic Kriging

We consider multiobjective simulation optimization problems, where several conflicting objectives are optimized simultaneously, and can only be observed via stochastic simulation. The goal is to find or approximate a (discrete) set of Pareto-optimal solutions that reveal the essential trade-offs between the objectives, where optimality means that no objective can be improved without deteriorating the quality of any other objective. The noise in the observed performance may lead to two possible misclassification errors: solutions that are truly Pareto-optimal can be wrongly considered dominated, and solutions that are truly dominated can be wrongly considered Pareto-optimal. We propose a Bayesian multiobjective ranking and selection method to reduce the number of errors when identifying the solutions with the true best expected performance. We use stochastic kriging metamodels to build reliable predictive distributions of the objectives, and exploit this information in two efficient screening procedures and two novel sampling criteria. We use these in a sequential sampling algorithm to decide how to allocate samples. Experimental results show that the proposed method only requires a small fraction of samples compared to the standard allocation method, and it's competitive against the state-of-the-art, with the exploitation of the correlation structure being the dominant contributor to the improvement.

Constrained multi-objective optimization of process design parameters in settings with scarce data: an application to adhesive bonding

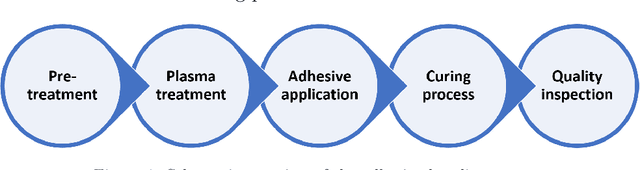
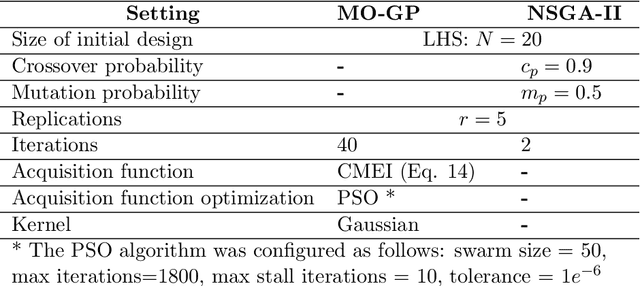
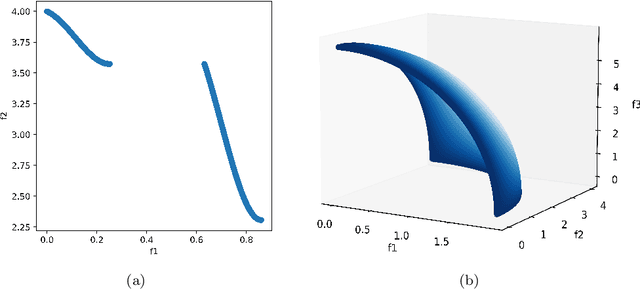
Adhesive joints are increasingly used in industry for a wide variety of applications because of their favorable characteristics such as high strength-to-weight ratio, design flexibility, limited stress concentrations, planar force transfer, good damage tolerance and fatigue resistance. Finding the optimal process parameters for an adhesive bonding process is challenging: the optimization is inherently multi-objective (aiming to maximize break strength while minimizing cost) and constrained (the process should not result in any visual damage to the materials, and stress tests should not result in failures that are adhesion-related). Real life physical experiments in the lab are expensive to perform; traditional evolutionary approaches (such as genetic algorithms) are then ill-suited to solve the problem, due to the prohibitive amount of experiments required for evaluation. In this research, we successfully applied specific machine learning techniques (Gaussian Process Regression and Logistic Regression) to emulate the objective and constraint functions based on a limited amount of experimental data. The techniques are embedded in a Bayesian optimization algorithm, which succeeds in detecting Pareto-optimal process settings in a highly efficient way (i.e., requiring a limited number of extra experiments).

Multi-objective simulation optimization of the adhesive bonding process of materials

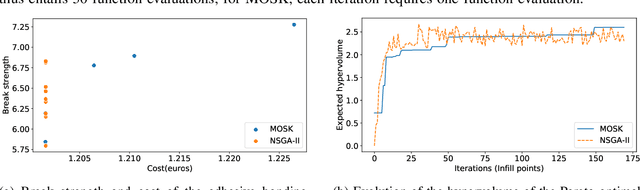
Automotive companies are increasingly looking for ways to make their products lighter, using novel materials and novel bonding processes to join these materials together. Finding the optimal process parameters for such adhesive bonding process is challenging. In this research, we successfully applied Bayesian optimization using Gaussian Process Regression and Logistic Regression, to efficiently (i.e., requiring few experiments) guide the design of experiments to the Pareto-optimal process parameter settings.

A survey on multi-objective hyperparameter optimization algorithms for Machine Learning

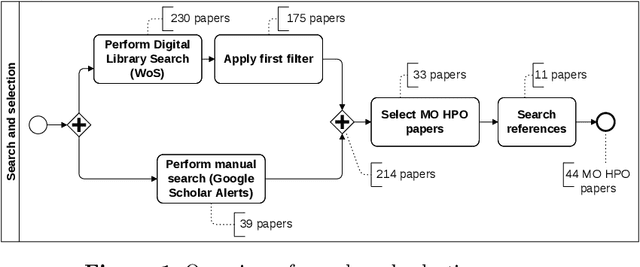
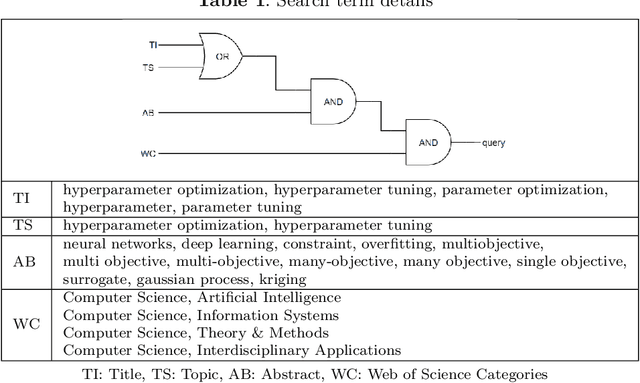
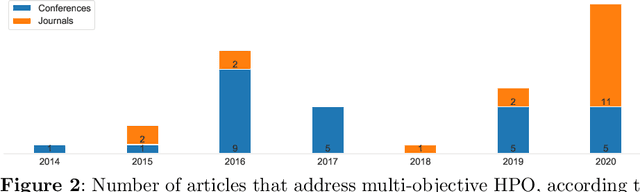
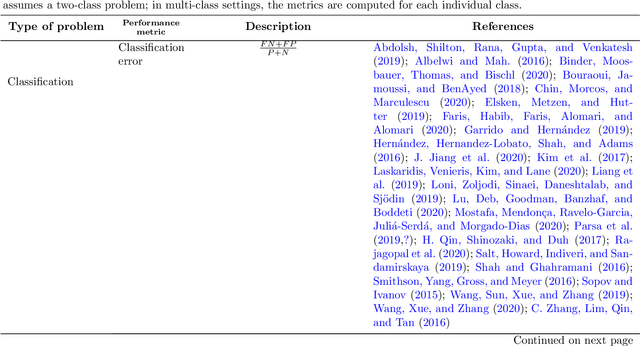
Hyperparameter optimization (HPO) is a necessary step to ensure the best possible performance of Machine Learning (ML) algorithms. Several methods have been developed to perform HPO; most of these are focused on optimizing one performance measure (usually an error-based measure), and the literature on such single-objective HPO problems is vast. Recently, though, algorithms have appeared which focus on optimizing multiple conflicting objectives simultaneously. This article presents a systematic survey of the literature published between 2014 and 2020 on multi-objective HPO algorithms, distinguishing between metaheuristic-based algorithms, metamodel-based algorithms, and approaches using a mixture of both. We also discuss the quality metrics used to compare multi-objective HPO procedures and present future research directions.