Multi-objective hyperparameter optimization with performance uncertainty

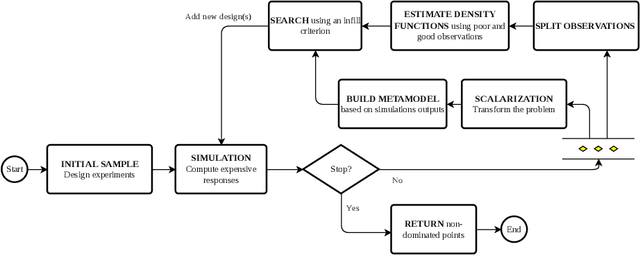
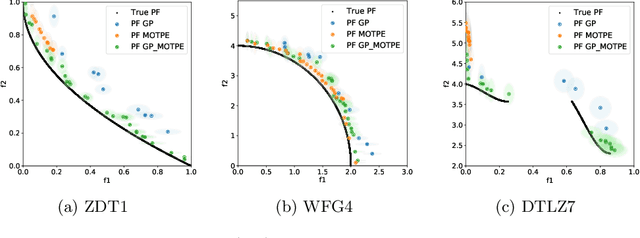
The performance of any Machine Learning (ML) algorithm is impacted by the choice of its hyperparameters. As training and evaluating a ML algorithm is usually expensive, the hyperparameter optimization (HPO) method needs to be computationally efficient to be useful in practice. Most of the existing approaches on multi-objective HPO use evolutionary strategies and metamodel-based optimization. However, few methods have been developed to account for uncertainty in the performance measurements. This paper presents results on multi-objective hyperparameter optimization with uncertainty on the evaluation of ML algorithms. We combine the sampling strategy of Tree-structured Parzen Estimators (TPE) with the metamodel obtained after training a Gaussian Process Regression (GPR) with heterogeneous noise. Experimental results on three analytical test functions and three ML problems show the improvement over multi-objective TPE and GPR, achieved with respect to the hypervolume indicator.

Constrained multi-objective optimization of process design parameters in settings with scarce data: an application to adhesive bonding

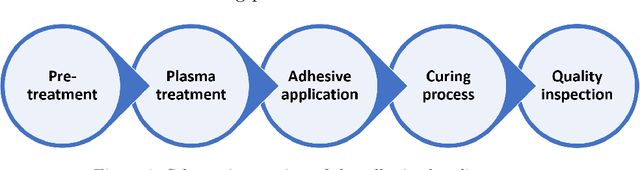
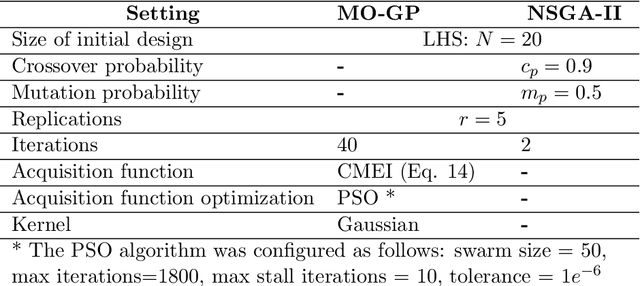
Adhesive joints are increasingly used in industry for a wide variety of applications because of their favorable characteristics such as high strength-to-weight ratio, design flexibility, limited stress concentrations, planar force transfer, good damage tolerance and fatigue resistance. Finding the optimal process parameters for an adhesive bonding process is challenging: the optimization is inherently multi-objective (aiming to maximize break strength while minimizing cost) and constrained (the process should not result in any visual damage to the materials, and stress tests should not result in failures that are adhesion-related). Real life physical experiments in the lab are expensive to perform; traditional evolutionary approaches (such as genetic algorithms) are then ill-suited to solve the problem, due to the prohibitive amount of experiments required for evaluation. In this research, we successfully applied specific machine learning techniques (Gaussian Process Regression and Logistic Regression) to emulate the objective and constraint functions based on a limited amount of experimental data. The techniques are embedded in a Bayesian optimization algorithm, which succeeds in detecting Pareto-optimal process settings in a highly efficient way (i.e., requiring a limited number of extra experiments).

Multi-objective simulation optimization of the adhesive bonding process of materials

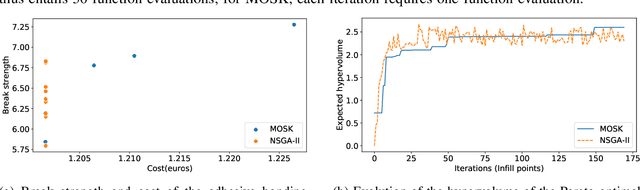
Automotive companies are increasingly looking for ways to make their products lighter, using novel materials and novel bonding processes to join these materials together. Finding the optimal process parameters for such adhesive bonding process is challenging. In this research, we successfully applied Bayesian optimization using Gaussian Process Regression and Logistic Regression, to efficiently (i.e., requiring few experiments) guide the design of experiments to the Pareto-optimal process parameter settings.

A survey on multi-objective hyperparameter optimization algorithms for Machine Learning

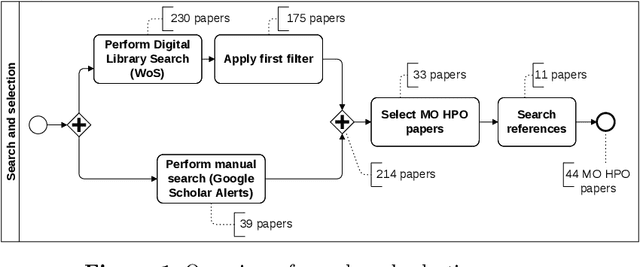
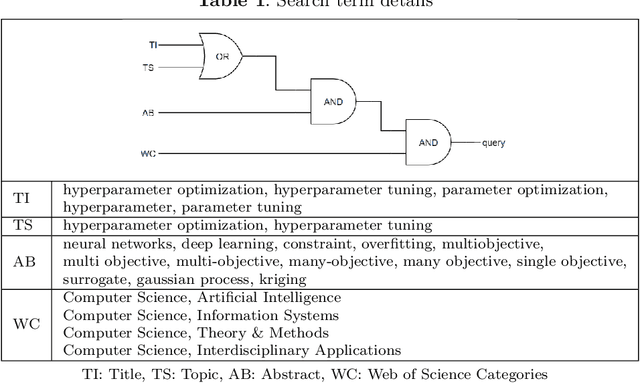
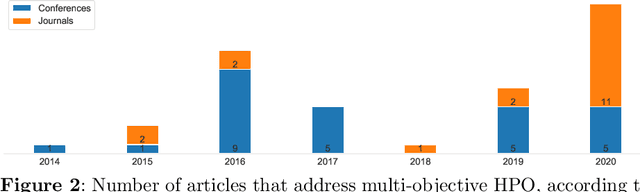
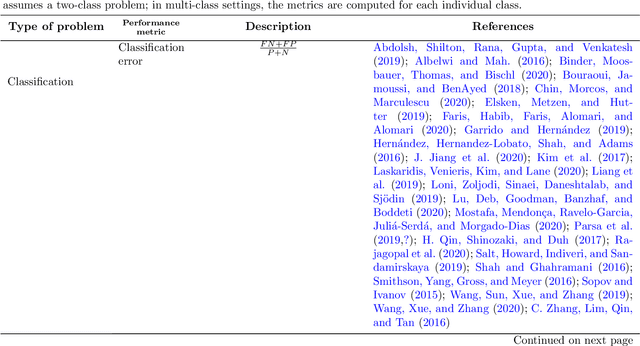
Hyperparameter optimization (HPO) is a necessary step to ensure the best possible performance of Machine Learning (ML) algorithms. Several methods have been developed to perform HPO; most of these are focused on optimizing one performance measure (usually an error-based measure), and the literature on such single-objective HPO problems is vast. Recently, though, algorithms have appeared which focus on optimizing multiple conflicting objectives simultaneously. This article presents a systematic survey of the literature published between 2014 and 2020 on multi-objective HPO algorithms, distinguishing between metaheuristic-based algorithms, metamodel-based algorithms, and approaches using a mixture of both. We also discuss the quality metrics used to compare multi-objective HPO procedures and present future research directions.