Specification-Oriented Automatic Design of Topologically Agnostic Antenna Structure

Design of antennas for modern applications is a challenging task that combines cognition-driven development of topology intertwined with tuning of its parameters using rigorous numerical optimization. However, the process can be streamlined by neglecting the engineering insight in favor of automatic de-termination of structure geometry. In this work, a specification-oriented design of topologically agnostic antenna is considered. The radiator is developed using a bi-stage algorithm that involves min-max classification of randomly-generated topologies followed by local tuning of the promising designs using a trust-region optimization applied to a feature-based representation of the structure frequency response. The automatically generated antenna is characterized by -10 dB bandwidth of over 600 MHz w.r.t. the center frequency of 6.5 GHz and a dual-lobe radiation pattern. The obtained performance figures make the radiator of use for in-door positioning applications. The design method has been favorably compared against the frequency-based trust-region optimization.

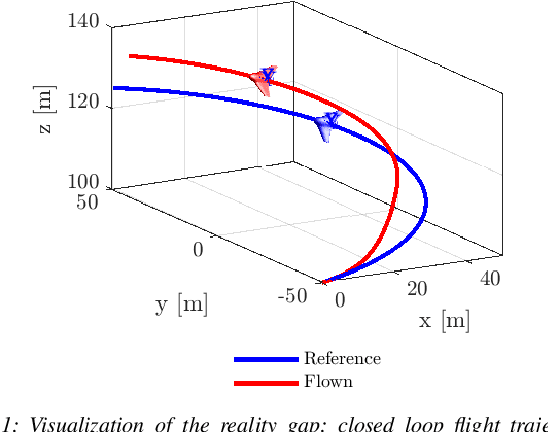
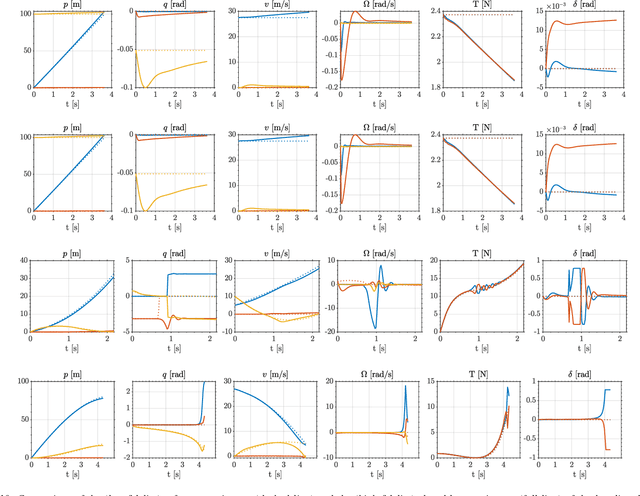
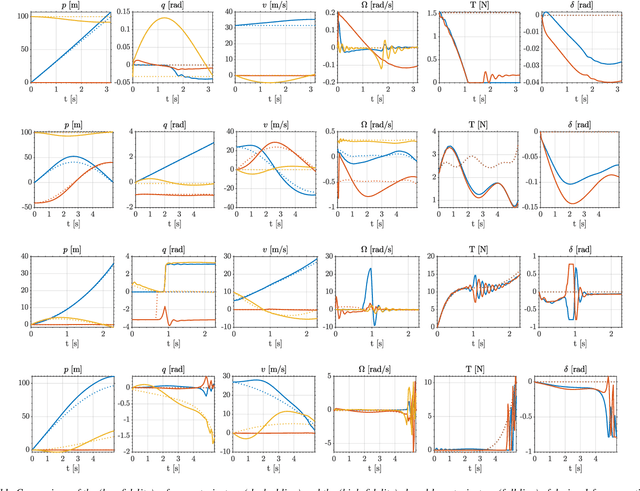
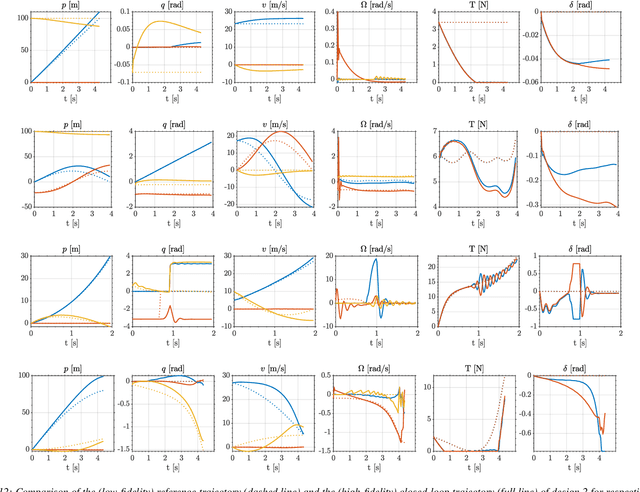
Introducing DAIMYO: a first-time-right dynamic design architecture and its application to tail-sitter UAS development

In recent years, there has been a notable evolution in various multidisciplinary design methodologies for dynamic systems. Among these approaches, a noteworthy concept is that of concurrent conceptual and control design or co-design. This approach involves the tuning of feedforward and/or feedback control strategies in conjunction with the conceptual design of the dynamic system. The primary aim is to discover integrated solutions that surpass those attainable through a disjointed or decoupled approach. This concurrent design paradigm exhibits particular promise in the context of hybrid unmanned aerial systems (UASs), such as tail-sitters, where the objectives of versatility (driven by control considerations) and efficiency (influenced by conceptual design) often present conflicting demands. Nevertheless, a persistent challenge lies in the potential disparity between the theoretical models that underpin the design process and the real-world operational environment, the so-called reality gap. Such disparities can lead to suboptimal performance when the designed system is deployed in reality. To address this issue, this paper introduces DAIMYO, a novel design architecture that incorporates a high-fidelity environment, which emulates real-world conditions, into the procedure in pursuit of a `first-time-right' design. The outcome of this innovative approach is a design procedure that yields versatile and efficient UAS designs capable of withstanding the challenges posed by the reality gap.

Bayesian Optimization for Non-Convex Two-Stage Stochastic Optimization Problems

Bayesian optimization is a sample-efficient method for solving expensive, black-box optimization problems. Stochastic programming concerns optimization under uncertainty where, typically, average performance is the quantity of interest. In the first stage of a two-stage problem, here-and-now decisions must be made in the face of this uncertainty, while in the second stage, wait-and-see decisions are made after the uncertainty has been resolved. Many methods in stochastic programming assume that the objective is cheap to evaluate and linear or convex. In this work, we apply Bayesian optimization to solve non-convex, two-stage stochastic programs which are expensive to evaluate. We formulate a knowledge-gradient-based acquisition function to jointly optimize the first- and second-stage variables, establish a guarantee of asymptotic consistency and provide a computationally efficient approximation. We demonstrate comparable empirical results to an alternative we formulate which alternates its focus between the two variable types, and superior empirical results over the standard, naive, two-step benchmark. We show that differences in the dimension and length scales between the variable types can lead to inefficiencies of the two-step algorithm, while the joint and alternating acquisition functions perform well in all problems tested. Experiments are conducted on both synthetic and real-world examples.

Data-Efficient Interactive Multi-Objective Optimization Using ParEGO

Multi-objective optimization is a widely studied problem in diverse fields, such as engineering and finance, that seeks to identify a set of non-dominated solutions that provide optimal trade-offs among competing objectives. However, the computation of the entire Pareto front can become prohibitively expensive, both in terms of computational resources and time, particularly when dealing with a large number of objectives. In practical applications, decision-makers (DMs) will select a single solution of the Pareto front that aligns with their preferences to be implemented; thus, traditional multi-objective algorithms invest a lot of budget sampling solutions that are not interesting for the DM. In this paper, we propose two novel algorithms that employ Gaussian Processes and advanced discretization methods to efficiently locate the most preferred region of the Pareto front in expensive-to-evaluate problems. Our approach involves interacting with the decision-maker to guide the optimization process towards their preferred trade-offs. Our experimental results demonstrate that our proposed algorithms are effective in finding non-dominated solutions that align with the decision-maker's preferences while maintaining computational efficiency.

Trieste: Efficiently Exploring The Depths of Black-box Functions with TensorFlow

We present Trieste, an open-source Python package for Bayesian optimization and active learning benefiting from the scalability and efficiency of TensorFlow. Our library enables the plug-and-play of popular TensorFlow-based models within sequential decision-making loops, e.g. Gaussian processes from GPflow or GPflux, or neural networks from Keras. This modular mindset is central to the package and extends to our acquisition functions and the internal dynamics of the decision-making loop, both of which can be tailored and extended by researchers or engineers when tackling custom use cases. Trieste is a research-friendly and production-ready toolkit backed by a comprehensive test suite, extensive documentation, and available at https://github.com/secondmind-labs/trieste.

$\{\text{PF}\}^2\text{ES}$: Parallel Feasible Pareto Frontier Entropy Search for Multi-Objective Bayesian Optimization Under Unknown Constraints

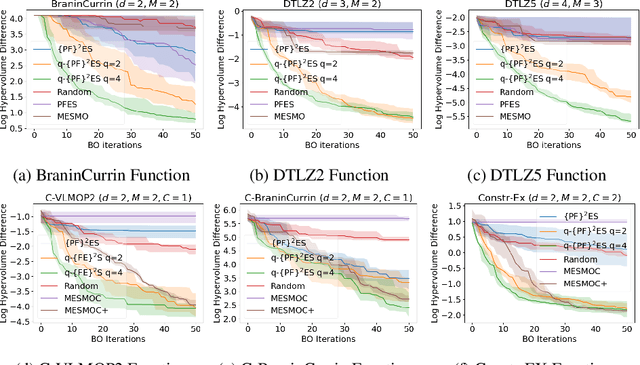
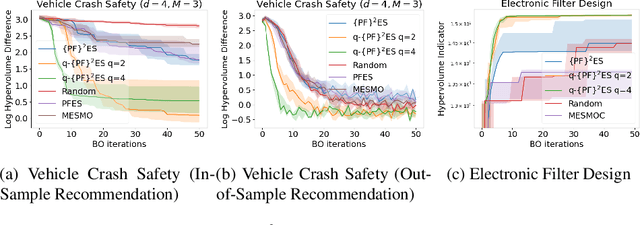
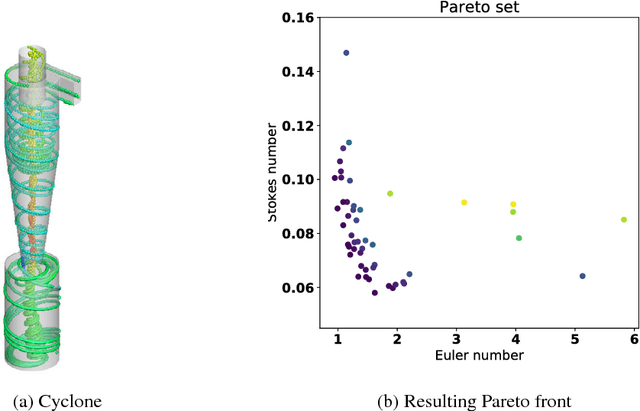
We present Parallel Feasible Pareto Frontier Entropy Search ($\{\text{PF}\}^2$ES) -- a novel information-theoretic acquisition function for multi-objective Bayesian optimization. Although information-theoretic approaches regularly provide state-of-the-art optimization, they are not yet widely used in the context of constrained multi-objective optimization. Due to the complexity of characterizing mutual information between candidate evaluations and (feasible) Pareto frontiers, existing approaches must employ severe approximations that significantly hamper their performance. By instead using a variational lower bound, $\{\text{PF}\}^2$ES provides a low cost and accurate estimate of the mutual information for the parallel setting (where multiple evaluations must be chosen for each optimization step). Moreover, we are able to interpret our proposed acquisition function by exploring direct links with other popular multi-objective acquisition functions. We benchmark $\{\text{PF}\}^2$ES across synthetic and real-life problems, demonstrating its competitive performance for batch optimization across synthetic and real-world problems including vehicle and electronic filter design.

Investigating the significance of adversarial attacks and their relation to interpretability for radar-based human activity recognition systems

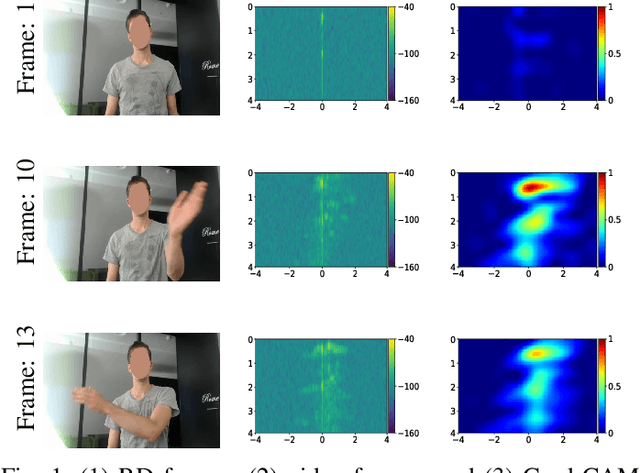
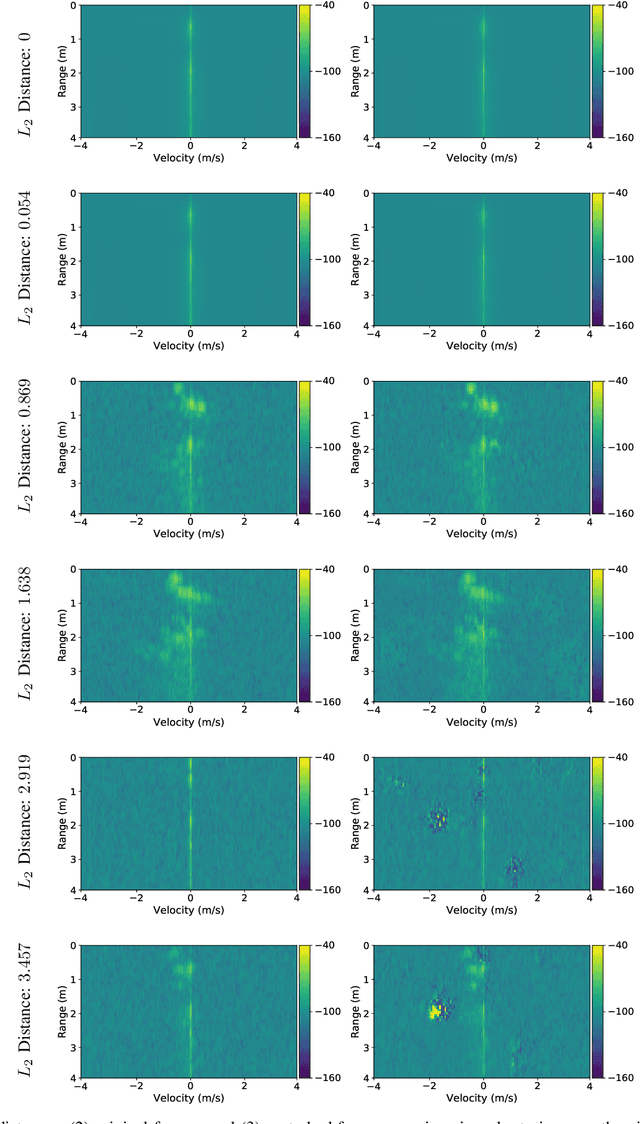
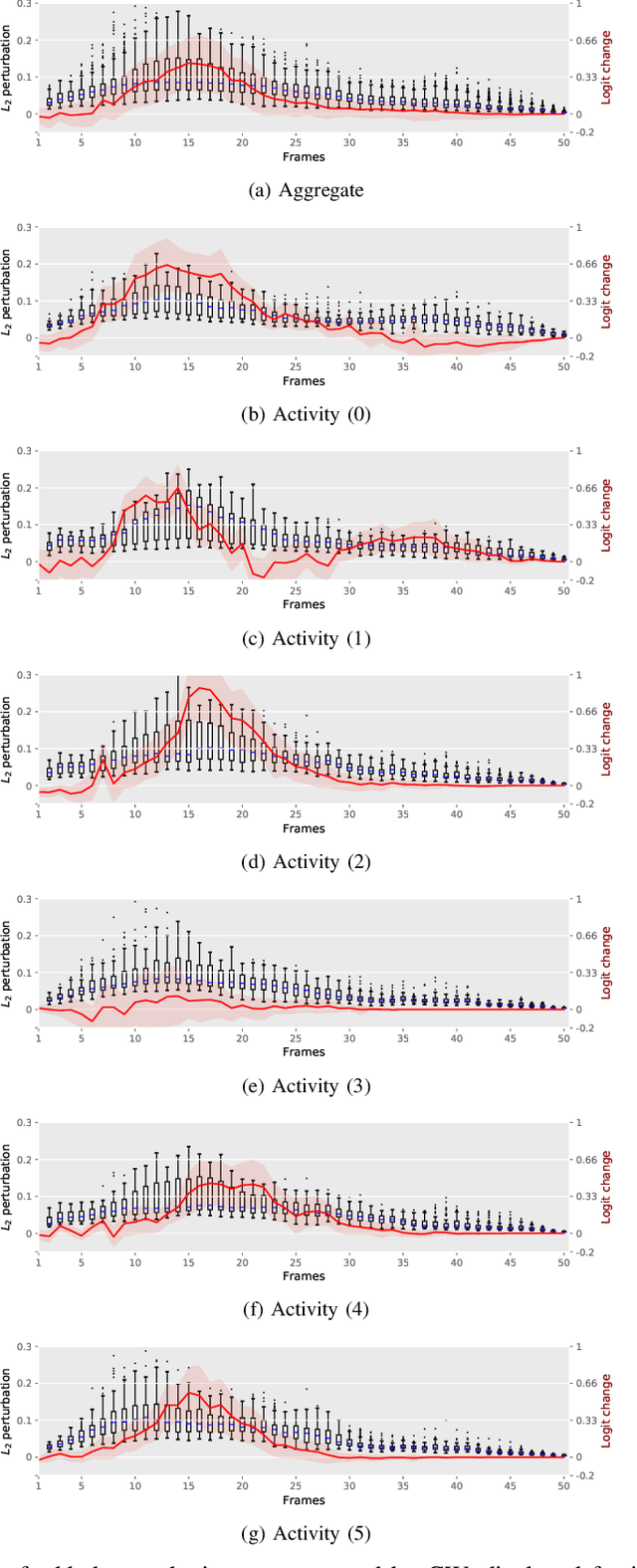
Given their substantial success in addressing a wide range of computer vision challenges, Convolutional Neural Networks (CNNs) are increasingly being used in smart home applications, with many of these applications relying on the automatic recognition of human activities. In this context, low-power radar devices have recently gained in popularity as recording sensors, given that the usage of these devices allows mitigating a number of privacy concerns, a key issue when making use of conventional video cameras. Another concern that is often cited when designing smart home applications is the resilience of these applications against cyberattacks. It is, for instance, well-known that the combination of images and CNNs is vulnerable against adversarial examples, mischievous data points that force machine learning models to generate wrong classifications during testing time. In this paper, we investigate the vulnerability of radar-based CNNs to adversarial attacks, and where these radar-based CNNs have been designed to recognize human gestures. Through experiments with four unique threat models, we show that radar-based CNNs are susceptible to both white- and black-box adversarial attacks. We also expose the existence of an extreme adversarial attack case, where it is possible to change the prediction made by the radar-based CNNs by only perturbing the padding of the inputs, without touching the frames where the action itself occurs. Moreover, we observe that gradient-based attacks exercise perturbation not randomly, but on important features of the input data. We highlight these important features by making use of Grad-CAM, a popular neural network interpretability method, hereby showing the connection between adversarial perturbation and prediction interpretability.

GPflowOpt: A Bayesian Optimization Library using TensorFlow

A novel Python framework for Bayesian optimization known as GPflowOpt is introduced. The package is based on the popular GPflow library for Gaussian processes, leveraging the benefits of TensorFlow including automatic differentiation, parallelization and GPU computations for Bayesian optimization. Design goals focus on a framework that is easy to extend with custom acquisition functions and models. The framework is thoroughly tested and well documented, and provides scalability. The current released version of GPflowOpt includes some standard single-objective acquisition functions, the state-of-the-art max-value entropy search, as well as a Bayesian multi-objective approach. Finally, it permits easy use of custom modeling strategies implemented in GPflow.

Hypervolume-based Multi-objective Bayesian Optimization with Student-t Processes

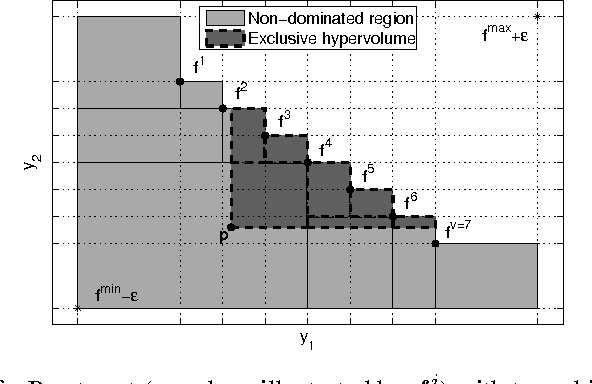
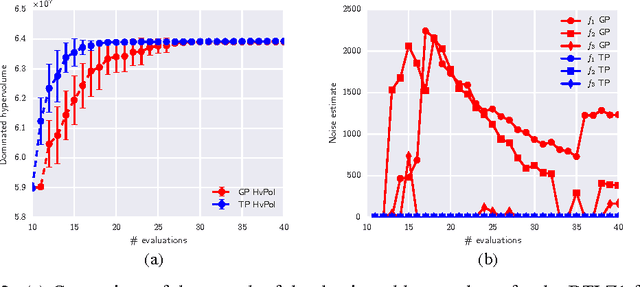
Student-$t$ processes have recently been proposed as an appealing alternative non-parameteric function prior. They feature enhanced flexibility and predictive variance. In this work the use of Student-$t$ processes are explored for multi-objective Bayesian optimization. In particular, an analytical expression for the hypervolume-based probability of improvement is developed for independent Student-$t$ process priors of the objectives. Its effectiveness is shown on a multi-objective optimization problem which is known to be difficult with traditional Gaussian processes.

Active Learning for Approximation of Expensive Functions with Normal Distributed Output Uncertainty

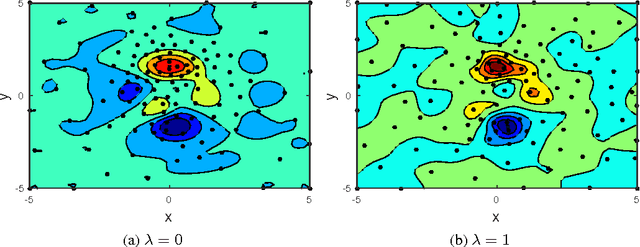
When approximating a black-box function, sampling with active learning focussing on regions with non-linear responses tends to improve accuracy. We present the FLOLA-Voronoi method introduced previously for deterministic responses, and theoretically derive the impact of output uncertainty. The algorithm automatically puts more emphasis on exploration to provide more information to the models.