GPflowOpt: A Bayesian Optimization Library using TensorFlow

A novel Python framework for Bayesian optimization known as GPflowOpt is introduced. The package is based on the popular GPflow library for Gaussian processes, leveraging the benefits of TensorFlow including automatic differentiation, parallelization and GPU computations for Bayesian optimization. Design goals focus on a framework that is easy to extend with custom acquisition functions and models. The framework is thoroughly tested and well documented, and provides scalability. The current released version of GPflowOpt includes some standard single-objective acquisition functions, the state-of-the-art max-value entropy search, as well as a Bayesian multi-objective approach. Finally, it permits easy use of custom modeling strategies implemented in GPflow.

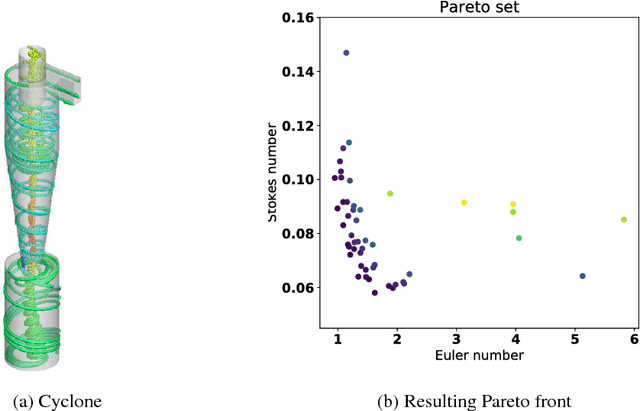
Hypervolume-based Multi-objective Bayesian Optimization with Student-t Processes

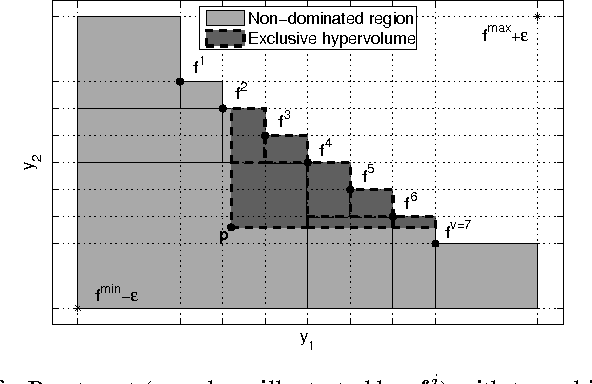
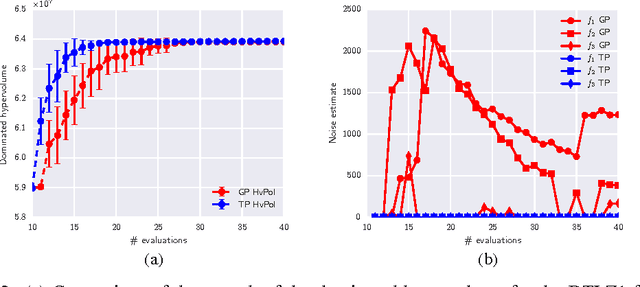
Student-$t$ processes have recently been proposed as an appealing alternative non-parameteric function prior. They feature enhanced flexibility and predictive variance. In this work the use of Student-$t$ processes are explored for multi-objective Bayesian optimization. In particular, an analytical expression for the hypervolume-based probability of improvement is developed for independent Student-$t$ process priors of the objectives. Its effectiveness is shown on a multi-objective optimization problem which is known to be difficult with traditional Gaussian processes.

Active Learning for Approximation of Expensive Functions with Normal Distributed Output Uncertainty

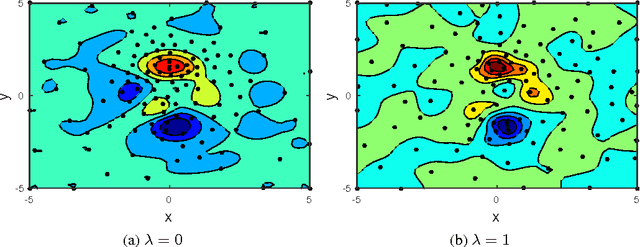
When approximating a black-box function, sampling with active learning focussing on regions with non-linear responses tends to improve accuracy. We present the FLOLA-Voronoi method introduced previously for deterministic responses, and theoretically derive the impact of output uncertainty. The algorithm automatically puts more emphasis on exploration to provide more information to the models.

Fast Calculation of the Knowledge Gradient for Optimization of Deterministic Engineering Simulations

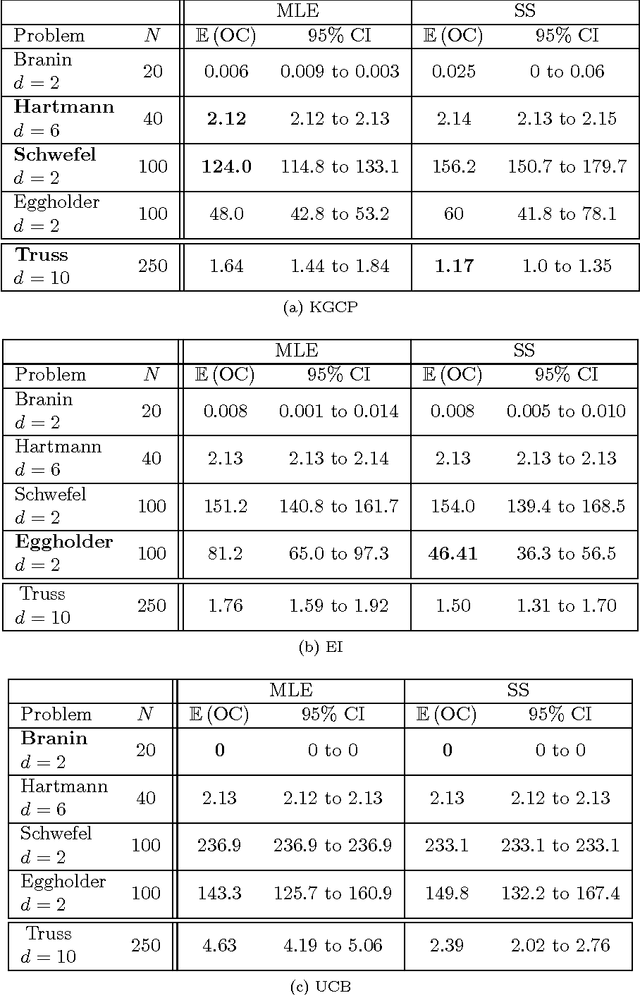
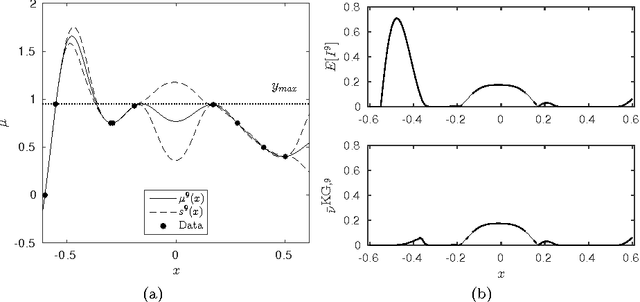
A novel efficient method for computing the Knowledge-Gradient policy for Continuous Parameters (KGCP) for deterministic optimization is derived. The differences with Expected Improvement (EI), a popular choice for Bayesian optimization of deterministic engineering simulations, are explored. Both policies and the Upper Confidence Bound (UCB) policy are compared on a number of benchmark functions including a problem from structural dynamics. It is empirically shown that KGCP has similar performance as the EI policy for many problems, but has better convergence properties for complex (multi-modal) optimization problems as it emphasizes more on exploration when the model is confident about the shape of optimal regions. In addition, the relationship between Maximum Likelihood Estimation (MLE) and slice sampling for estimation of the hyperparameters of the underlying models, and the complexity of the problem at hand, is studied.